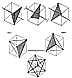
Fig. 462.00
 Rotation of Triangle in Cube
Rotation of Triangle in Cube
 Fig. 462.00 |
462.00  Rotation of Triangle in Cube
Rotation of Triangle in Cube
|

|
462.01
 To comprehend the complex of transformings demonstrated
by the jitterbug
we may identify each of the eight triangles of the vector
equilibrium with the eight small
cubes which comprise a two-frequency large cube's eight
corners. When the jitterbug
transforms into an octahedron, the jitterbug vector
equilibrium's six square faces disappear
leaving only the eight triangles of the vector equilibrium,
each of which has moved
inwardly at a symmetrical rate toward the common center
of the vector equilibrium as the
squares disappear and the triangles approach one another
until their respective three edges
each become congruent with one another, thus doubling
their vector edges together in
paralleled congruence. Since each of the eight triangles
behaved the same way as the
others we can now study how one behaved and we find
that each triangle "did its thing"
entirely within the domain of one of the eight cubes
of the two-frequency big cube. Thus
we learn that a triangle can rotate within the topological
lines of a cube with the triangle's
three corners being guided by the cube's edges.
To comprehend the complex of transformings demonstrated
by the jitterbug
we may identify each of the eight triangles of the vector
equilibrium with the eight small
cubes which comprise a two-frequency large cube's eight
corners. When the jitterbug
transforms into an octahedron, the jitterbug vector
equilibrium's six square faces disappear
leaving only the eight triangles of the vector equilibrium,
each of which has moved
inwardly at a symmetrical rate toward the common center
of the vector equilibrium as the
squares disappear and the triangles approach one another
until their respective three edges
each become congruent with one another, thus doubling
their vector edges together in
paralleled congruence. Since each of the eight triangles
behaved the same way as the
others we can now study how one behaved and we find
that each triangle "did its thing"
entirely within the domain of one of the eight cubes
of the two-frequency big cube. Thus
we learn that a triangle can rotate within the topological
lines of a cube with the triangle's
three corners being guided by the cube's edges.
|

|
462.02
 Wave-propagating action is cyclically generated by
a cube with a triangle
rotating in it.
Wave-propagating action is cyclically generated by
a cube with a triangle
rotating in it.
|

|
463.00
 Diagonal of Cube as Wave-Propagation Model
Diagonal of Cube as Wave-Propagation Model
|
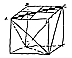 Fig. 463.01 |
463.01
 There are no straight lines, only waves resembling
them. In the diagram, any
zigzag path from A to C equals the sum of the sides
AB and BC. If the zigzag is of high
frequency, it may look like a diagonal that should be
shorter than ABC. It is not.
There are no straight lines, only waves resembling
them. In the diagram, any
zigzag path from A to C equals the sum of the sides
AB and BC. If the zigzag is of high
frequency, it may look like a diagonal that should be
shorter than ABC. It is not.
|

|
463.02
 As the triangle rotates in the cube, it goes from
being congruent with the
positive tetrahedron to being congruent with the negative
tetrahedron. It is an oscillating
system in which, as the triangles rotate, their corners
describe arcs (see
Sec. 464.02)
which convert the cube's 12 edges from quasistraight
lines to 12 arcs which altogether
produce a dynamically described sphere (a spherical
cube) which makes each cube to
appear to be swelling locally. But there is a pulsation
arc-motion lag in it exactly like our
dropping a stone in the water and getting a planar pattern
for a wave
(see Sec. 505.30),
but in this model we get an omnidirectional wave pulsation.
This is the first time man has
been able to have a conceptual picture of a local electromagnetic
wave disturbance.
As the triangle rotates in the cube, it goes from
being congruent with the
positive tetrahedron to being congruent with the negative
tetrahedron. It is an oscillating
system in which, as the triangles rotate, their corners
describe arcs (see
Sec. 464.02)
which convert the cube's 12 edges from quasistraight
lines to 12 arcs which altogether
produce a dynamically described sphere (a spherical
cube) which makes each cube to
appear to be swelling locally. But there is a pulsation
arc-motion lag in it exactly like our
dropping a stone in the water and getting a planar pattern
for a wave
(see Sec. 505.30),
but in this model we get an omnidirectional wave pulsation.
This is the first time man has
been able to have a conceptual picture of a local electromagnetic
wave disturbance.
|

|
463.03
 The cube oscillates from the static condition to the
dynamic, from the
potential to the radiant. As it becomes a wave, the
linear becomes the second-power rate
of grc wth. The sum of the squares of the two legs =
the square of the hypotenuse=the
wave. The 12 edges of the cube become the six diagonals
of the tetrahedron by virtue of
the hypotenuse: the tetrahedron is the normal condition
of the real (electromagnetic)
world. (See Sec. 982.21.)
The cube oscillates from the static condition to the
dynamic, from the
potential to the radiant. As it becomes a wave, the
linear becomes the second-power rate
of grc wth. The sum of the squares of the two legs =
the square of the hypotenuse=the
wave. The 12 edges of the cube become the six diagonals
of the tetrahedron by virtue of
the hypotenuse: the tetrahedron is the normal condition
of the real (electromagnetic)
world. (See Sec. 982.21.)
|

|
463.04
 There is an extraordinary synergetic realization as
a consequence of
correlating (a) the arc-describing, edge-pulsing of
cubes generated by the eight triangles
rotating in the spheres whose arcs describe the spherical
cube (which is a sphere whose
volume is 2.714__approximately three__times that of the
cube) and (b) the deliberately
nonstraight line transformation model
(see Sec. 522),
in which the edges of the cube
become the six wavilinear diagonals of the cube, which
means the cube transforming into a
tetrahedron. Synergetically, we have the tetrahedron
of volume one and the cube of
volume three__as considered separately__in no way predicting
that the cube would be
transformed into an electromagnetic-wave-propagating
tetrahedron. This is an energy
compacting of 3
There is an extraordinary synergetic realization as
a consequence of
correlating (a) the arc-describing, edge-pulsing of
cubes generated by the eight triangles
rotating in the spheres whose arcs describe the spherical
cube (which is a sphere whose
volume is 2.714__approximately three__times that of the
cube) and (b) the deliberately
nonstraight line transformation model
(see Sec. 522),
in which the edges of the cube
become the six wavilinear diagonals of the cube, which
means the cube transforming into a
tetrahedron. Synergetically, we have the tetrahedron
of volume one and the cube of
volume three__as considered separately__in no way predicting
that the cube would be
transformed into an electromagnetic-wave-propagating
tetrahedron. This is an energy
compacting of 3 1; but sum-totally this means an energetic-volumetric
contraction from
the spherical cube's volume of 8.142 to the tetrahedron's
one, which energetic compacting
serves re-exp__nsively to power the electromagnetic-wave-propagating
behavior of the
wavilinearedged tetrahedron.
(See Sec. 982.30.) 1; but sum-totally this means an energetic-volumetric
contraction from
the spherical cube's volume of 8.142 to the tetrahedron's
one, which energetic compacting
serves re-exp__nsively to power the electromagnetic-wave-propagating
behavior of the
wavilinearedged tetrahedron.
(See Sec. 982.30.)
|

|
463.05
 We really find, learning synergetically, from the
combined behaviors of the
tetrahedron, the cube, and the deliberately-nonstraight-line
cubical transformation into a
tetrahedron, how the eight cubical corners are self-truncated
to produce the vector
equilibrium within the allspace-filling cubical isotropic-vector-matrix
reference frame; in so
doing, the local vacatings of the myriad complex of
closest-packing cube truncations
produce a "fallout" of all the "exterior octahedra"
as a consequence of the simultaneous
truncation of the eight comers of the eight cubes surrounding
any one point. As we learn
elsewhere
(see Sec. 1032.10),
the exterior octahedron
is the contracted vector equilibriurn
and is one of the spaces between spheres; the octahedron
thus becomes available as the
potential alternate new sphere when the old spheres
become spaces. The octahedra thus
serve in the allspace-filling exchange of spheres and
spaces (see Sec. 970.20).
We really find, learning synergetically, from the
combined behaviors of the
tetrahedron, the cube, and the deliberately-nonstraight-line
cubical transformation into a
tetrahedron, how the eight cubical corners are self-truncated
to produce the vector
equilibrium within the allspace-filling cubical isotropic-vector-matrix
reference frame; in so
doing, the local vacatings of the myriad complex of
closest-packing cube truncations
produce a "fallout" of all the "exterior octahedra"
as a consequence of the simultaneous
truncation of the eight comers of the eight cubes surrounding
any one point. As we learn
elsewhere
(see Sec. 1032.10),
the exterior octahedron
is the contracted vector equilibriurn
and is one of the spaces between spheres; the octahedron
thus becomes available as the
potential alternate new sphere when the old spheres
become spaces. The octahedra thus
serve in the allspace-filling exchange of spheres and
spaces (see Sec. 970.20).
|

|
464.00
 Triangle in Cube as Energetic Model
Triangle in Cube as Energetic Model |
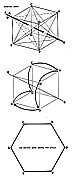 Fig. 464.01 |
464.01
 The triangle CDE formed by connecting the diagonals
of the three adjacent
square faces surrounding one corner, A, of the cube
defines the base triangular face of one
of the two tetrahedra always coexisting within, and
structurally permitting the stability of,
the otherwise unstable cubic form. The triangle GHF
formed by connecting the three
adjacent faces surrounding the B corner of the same
cube diametrically, i.e. polarly,
opposite the first triangulated corner, defines the
triangular face GHF of the other of the
two tetrahedra always coexisting within that and all
other cubes. The plane of the green
triangle CDE remains always parallel to the plane of
the red triangle GHF even though it
is rotated along and around the shaft AB (see drawings
section).
The triangle CDE formed by connecting the diagonals
of the three adjacent
square faces surrounding one corner, A, of the cube
defines the base triangular face of one
of the two tetrahedra always coexisting within, and
structurally permitting the stability of,
the otherwise unstable cubic form. The triangle GHF
formed by connecting the three
adjacent faces surrounding the B corner of the same
cube diametrically, i.e. polarly,
opposite the first triangulated corner, defines the
triangular face GHF of the other of the
two tetrahedra always coexisting within that and all
other cubes. The plane of the green
triangle CDE remains always parallel to the plane of
the red triangle GHF even though it
is rotated along and around the shaft AB (see drawings
section).
|

|
464.02
 If the first triangle CDE defined by the three diagonals
surrounding the A
corner of the cube is rotated on the axis forrned by
the diagonal leading from that corner
of the cube inwardly to its polarly opposite and oppositely
triangled B corner, the rotated
triangle maintains its attitude at right angles to its
axis, and its three vertexes move along
the three edges of the cube until the green triangle
reaches and become congruent with the
red base triangle of the axially opposite corner. Thereafter,
if the rotation continues in the
same circular direction, the same traveling triangle
will continue to travel pulsatingly, back
and forth, becoming alternately the base triangle of
the positive and then of the negative
tetrahedron. As the triangle returns from its first
trip away, its corners follow three
additional edges of the cube. As the vertexes of the
shuttling triangle follow the six cube
edges, their apexes protrude and describe spherical
arcs outwardly along the cubes' edges
running from cube corner to cube corner. Swift rotation
of the triangle's shaft not only
causes the triangle to shuttle back and forth, but also
to describe six of the 12 edges of the
spherical cube producing an equatorially spheroid pulsation.
The two equal tetrahedra are
not only oppositely oriented, but their respective volumetric
centers (positive and
negative) are congruent, being joined at their common
centers of volume, which coincide
with that of the containing cube. Because each cube
in the eight-cube, two-frequency big
cube has both a positive and a negative tetrahedron
in it, and because each tetrahedron has
four triangular faces, each cube has eight equilateral
triangular edges corresponding to the
12 diagonalling hypotenuses of each cube's six faces.
If the first triangle CDE defined by the three diagonals
surrounding the A
corner of the cube is rotated on the axis forrned by
the diagonal leading from that corner
of the cube inwardly to its polarly opposite and oppositely
triangled B corner, the rotated
triangle maintains its attitude at right angles to its
axis, and its three vertexes move along
the three edges of the cube until the green triangle
reaches and become congruent with the
red base triangle of the axially opposite corner. Thereafter,
if the rotation continues in the
same circular direction, the same traveling triangle
will continue to travel pulsatingly, back
and forth, becoming alternately the base triangle of
the positive and then of the negative
tetrahedron. As the triangle returns from its first
trip away, its corners follow three
additional edges of the cube. As the vertexes of the
shuttling triangle follow the six cube
edges, their apexes protrude and describe spherical
arcs outwardly along the cubes' edges
running from cube corner to cube corner. Swift rotation
of the triangle's shaft not only
causes the triangle to shuttle back and forth, but also
to describe six of the 12 edges of the
spherical cube producing an equatorially spheroid pulsation.
The two equal tetrahedra are
not only oppositely oriented, but their respective volumetric
centers (positive and
negative) are congruent, being joined at their common
centers of volume, which coincide
with that of the containing cube. Because each cube
in the eight-cube, two-frequency big
cube has both a positive and a negative tetrahedron
in it, and because each tetrahedron has
four triangular faces, each cube has eight equilateral
triangular edges corresponding to the
12 diagonalling hypotenuses of each cube's six faces.
|

|
464.03
 Each cube has four pairs of polarly opposite corners.
There are four co-
occurring, synchronously operative, triangularly shuttleable
systems within each cube; with
all of them synchronously operative, the cube's 12 edges
will be synchronously
accommodating__ 4 ×
6 = 24 __edge-arcings traveling 12
positively and 12 negatively, to
produce the profile of two spherical cubes, one positive
and one negative.
Each cube has four pairs of polarly opposite corners.
There are four co-
occurring, synchronously operative, triangularly shuttleable
systems within each cube; with
all of them synchronously operative, the cube's 12 edges
will be synchronously
accommodating__ 4 ×
6 = 24 __edge-arcings traveling 12
positively and 12 negatively, to
produce the profile of two spherical cubes, one positive
and one negative.
|

|
464.04
 Each vector equilibrium, when complemented by its
coexistent share of one-
eighth of its (concave) external octahedra, embraces
eight cubes, each of which has four
activable, axially shuttleable, electromagnetic-energygenerating
potentials.
Each vector equilibrium, when complemented by its
coexistent share of one-
eighth of its (concave) external octahedra, embraces
eight cubes, each of which has four
activable, axially shuttleable, electromagnetic-energygenerating
potentials.
|

|
464.05
 Eight of these triangular shuttle cubes may be completed
on each of the
vector equilibrium's eight triangular faces by adding
one 1/8th-Octa comer to each of
them. Each 1/8th-Octa corner consists of six A and six
B modules. As one such l/8th-Octa,
6A-6B moduled, 90°-apexed, equianglebased, isosceles
tetrahedron is added to any of the
vector equilibrium's eight triangular faces, which contain
the potential new nucleus__
which thus becomes a newborn active nucleus__when so
double-layer covered by the 12
A's and 12 B's energy modules, which altogether produce
a total of 24 energy modules
whenever the rotating triangle alternates its position,
which combined 24 modules
correspond to the 24 energy modules of one whole regular
tetrahedral event, which is the
quantum in nuclear physics.
Eight of these triangular shuttle cubes may be completed
on each of the
vector equilibrium's eight triangular faces by adding
one 1/8th-Octa comer to each of
them. Each 1/8th-Octa corner consists of six A and six
B modules. As one such l/8th-Octa,
6A-6B moduled, 90°-apexed, equianglebased, isosceles
tetrahedron is added to any of the
vector equilibrium's eight triangular faces, which contain
the potential new nucleus__
which thus becomes a newborn active nucleus__when so
double-layer covered by the 12
A's and 12 B's energy modules, which altogether produce
a total of 24 energy modules
whenever the rotating triangle alternates its position,
which combined 24 modules
correspond to the 24 energy modules of one whole regular
tetrahedral event, which is the
quantum in nuclear physics.
|

|
464.06
 The vector equilibrium's jitterbugging conceptually
manifests that any action
(and its inherent reaction force) applied to any system
always articulates a complex of
vector-equilibria, macro-micro jitterbugging, invllving
all the vector equilibria's ever
cosmically replete complenentations by their always
co-occurring internal and external
octahedra__all of which respond to the action by intertransforming
in concert from "space
nothingnesses" into closest-packed spherical "somethings,"
and vice versa, in a complex
threeway shuttle while propagating a total omniradiant
wave pulsation operating in unique
frequencies that in no-wise interfere with the always
omni-co-occurring cosmic gamut of
otherly frequenced cosmic vector-equilibria accommodations.
The vector equilibrium's jitterbugging conceptually
manifests that any action
(and its inherent reaction force) applied to any system
always articulates a complex of
vector-equilibria, macro-micro jitterbugging, invllving
all the vector equilibria's ever
cosmically replete complenentations by their always
co-occurring internal and external
octahedra__all of which respond to the action by intertransforming
in concert from "space
nothingnesses" into closest-packed spherical "somethings,"
and vice versa, in a complex
threeway shuttle while propagating a total omniradiant
wave pulsation operating in unique
frequencies that in no-wise interfere with the always
omni-co-occurring cosmic gamut of
otherly frequenced cosmic vector-equilibria accommodations.
|

|
464.07
 In contradistinction to the sphere, the tetrahedron
has the most surface with
the least volume of any symmetrical form. The total
available energy of a system is related
to its surface area, involving the second power of the
radius. E = Mc2. The mass
congruence of any two similar systems results in a synergetic
relationship with a second-
powering of cohesiveness of the joined systems. This
releases the fourfolded energy,
which no longer has the two tetrahedra's mass-interattraction
work to do, and this in turn
releases the energies outward to the tetrahedra's highest-capacity
surfaces. And since
surface functions as the electromagnetic-energy carrier,
and since the energy relayed to
their surfaces alternates from the positive to the negative
tetrahedron, and since the
distance between their surface centers is only two A
Module altitude wavelengths (each of
which two A Module altitudes constitute and serve as
one generalized electromagnetic
wavelength with generatable frequency beginning at two),
the rotation of the triangle
within the cube passes through the common energy centers
of the two tetrahedra and
delivers its content to the other base surface, after
which it pulses through center delivery
of the opposite charge to the other surface, which altogether
propagates potentially
exportable, frequency-determinate, electromagnetic energy.
The six cube-edge travelings
of the triangles' vertexes accomplished with each cycle
of the triangle-in-cube shuttle
coincides in number and is akin to the six vector edges
comprising one tetrahedral
quantum; the sixness of wavilinear and sometimes reangularly
redirected traveling employs
also the six basic degrees of freedom articulated by
each and every one cosmic event.
In contradistinction to the sphere, the tetrahedron
has the most surface with
the least volume of any symmetrical form. The total
available energy of a system is related
to its surface area, involving the second power of the
radius. E = Mc2. The mass
congruence of any two similar systems results in a synergetic
relationship with a second-
powering of cohesiveness of the joined systems. This
releases the fourfolded energy,
which no longer has the two tetrahedra's mass-interattraction
work to do, and this in turn
releases the energies outward to the tetrahedra's highest-capacity
surfaces. And since
surface functions as the electromagnetic-energy carrier,
and since the energy relayed to
their surfaces alternates from the positive to the negative
tetrahedron, and since the
distance between their surface centers is only two A
Module altitude wavelengths (each of
which two A Module altitudes constitute and serve as
one generalized electromagnetic
wavelength with generatable frequency beginning at two),
the rotation of the triangle
within the cube passes through the common energy centers
of the two tetrahedra and
delivers its content to the other base surface, after
which it pulses through center delivery
of the opposite charge to the other surface, which altogether
propagates potentially
exportable, frequency-determinate, electromagnetic energy.
The six cube-edge travelings
of the triangles' vertexes accomplished with each cycle
of the triangle-in-cube shuttle
coincides in number and is akin to the six vector edges
comprising one tetrahedral
quantum; the sixness of wavilinear and sometimes reangularly
redirected traveling employs
also the six basic degrees of freedom articulated by
each and every one cosmic event.
|

|
464.08
 Thus we realize conceptually the ever-self-regenerative,
omniidealized,
eternal integrity of the utterly metaphysical, timeless,
weightless, zerophase geometric
frame of transformations referencing function, which
is served by the vector equilibrium in
respect to which all the aberrational dimensioning of
all realization of the variety of
relative durations, sensorial lags, recalls, and imaginings
are formulatingly referenced to
differentiate out into the special-case local experiences
of the eternal scenario Universe,
which each of us identifies to ourselves as the "Shape
of Things" and which each
individual sees differently yet ever intuits to be rigorously
referenced to an invisibly perfect
prototype in pure principle, in respect to which only
approachable but never realizable
"understanding" of one of us by others occurs: "And
it Came to Pass."
Thus we realize conceptually the ever-self-regenerative,
omniidealized,
eternal integrity of the utterly metaphysical, timeless,
weightless, zerophase geometric
frame of transformations referencing function, which
is served by the vector equilibrium in
respect to which all the aberrational dimensioning of
all realization of the variety of
relative durations, sensorial lags, recalls, and imaginings
are formulatingly referenced to
differentiate out into the special-case local experiences
of the eternal scenario Universe,
which each of us identifies to ourselves as the "Shape
of Things" and which each
individual sees differently yet ever intuits to be rigorously
referenced to an invisibly perfect
prototype in pure principle, in respect to which only
approachable but never realizable
"understanding" of one of us by others occurs: "And
it Came to Pass."
|
| Next Section: 465.00 |