Allspace-Filling Tetrahedra
|
|
951.00
Allspace-Filling Tetrahedra
|
|
|
951.01
The tetrahedra that fill allspace by themselves are
all asymmetrical. They are
dynamic reality only-for-each-moment. Reality is always
asymmetrical.
|
|
|
951.10
Synergetic Allspace-Filling Tetrahedron: Synergetic
geometry has one
cosmically minimal, allspace-filling tetrahedron consisting
of only four A Quanta Modules
and two B Quanta Modules__six modules in all__whereas
the regular tetrahedron consists
of 24 such modules and the cube consists of 72. (See
Illus.
950.12.)
|
|
|
953.00
Mites and Sytes: Minimum Tetrahedra as Three-Module
Allspace Fillers
|
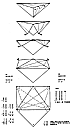 Fig. 953.10 |
953.10
Minimum Tetrahedron: Mite: Two A Quanta Modules and
one B Quanta
Module may be associated to define the allspace-filling
positive and negative sets of three
geometrically dissimilar, asymmetric, but unit volume
energy quanta modules which join
the volumetric center hearts of the octahedron and tetrahedron.
For economy of discourse,
we will give this minimum allspace-filling AAB complex
three-quanta module's
asymmetrical tetrahedron the name of Mite (as a contraction
of Minimum Tetrahedron,
allspace filler). (See drawings section.)
|
|
|
953.20
Positive or Negative: Mites can fill allspace. They
can be either positive (+)
or negative (-), affording a beautiful confirmation
of negative Universe. Each one can fill
allspace, but with quite different energy consequences.
Both the positive and negative
Mite Tetrahedra are comprised, respectively, of two
A Quanta Modules and one B Quanta
Module. In each Mite, one of the two A s is positive
and one is negative; the B must be
positive when the Mite is positive and negative when
the Mite is negative. The middle A
Quanta Module of the MB wedge-shaped sandwich is positive
when the Mite and its B
Quanta Module are negative. The Mite and its B Quanta
Module have like signs. The Mite
and its middle A Quanta Module have unlike signs.
|
|
|
953.21
If there were only positive Universe, there would
be only Sytes (see Sec.
953.40.
But Mites can be either plus or minus; they accommodate
both Universes, the
positive and the negative, as well as the half-positive
and half-negative, as manifestations
of fundamental complementarity. They are true rights
and lefts, not mirror images; they
are inside out and asymmetrical.
|
|
|
953.22
There is a noncongruent, ergo mutually exclusive,
tripartiteness (i.e., two As
and one B in a wedge sandwich) respectively unique to
either the positive or the negative
world. The positive model provides for the interchange
between the spheres and the
spaces.4 But the Mite permits the same kind of exchange
in negative Universe.
(Footnote 4: See Sec. 1032.10.) |
|
|
953.23
The cube as an allspace filler requires only a positive
world. The inside-out
cube is congruent with the outside-out cube. Whereas
the inside-out and outside-out
Mites are not congruent and refuse congruency.
|
|
|
953.24
Neither the tetrahedron nor the octahedron can be
put together with Mites.
But the allspace-filling rhombic dodecahedron and the
allspace-filling tetrakaidecahedron
can be exactly assembled with Mites. Their entire componentation
exclusively by Mites
tells us that either or both the rhombic dodecahedron
and the tetrakaidecahedron can
function in either the positive or the negative Universe.
|
|
|
953.25
The allspace-filling functions of the (+) or (-) AAB
three-module Mite
combines can operate either positively or negatively.
We can take a collection of the
positives or a collection of the negatives. If there
were only positive outside-out Universe,
it would require only one of the three alternate six-module,
allspace-filling tetrahedra (see
Sec.
953.40)
combined of two A (+), two A (-), one B
(+), and one B (-) to fill allspace
symmetrically and complementarily. But with both inside-out
and outside-out worlds, we
can fill all the outside-out world's space positively
and all the inside-out world's space
negatively, accommodating the inherent complementarity
symmetry requirements of the
macro-micro cosmic law of convex world and concave world,
while remembering all the
time that among all polyhedra only the tetrahedron can
turn itself inside out.
|
|
|
953.30
Tetrahedron as Three-Petaled Flower Bud: Positive
or negative means
that one is the inside-out of the other. To understand
the insideouting of tetrahedra, think
of the tetrahedron's four outside faces as being blue
and the four inside faces as being red.
If we split open any three edges leading to any one
of the tetrahedron's vertexes, the
tetrahedron will appear as a three-petaled flower bud,
just opening, with the triangular
petals hinging open around the common triangular base.
The opening of the outside-blue-
inside-red tetrahedron and the hinging of all its blue
bud's petals outwardly and
downwardly until they meet one another's edges below
the base, will result in the whole
tetrahedron's appearing to be red while its hidden interior
is blue. All the other
geometrical characteristics remain the same. If it is
a regular tetrahedron, all the parts of
the outside-red or the outside-blue regular tetrahedron
will register in absolute
congruence.
|
|
|
953.40
Symmetrical Tetrahedron: Syte: Two of the AAB allspace-filling,
three-
quanta module, asymmetric tetrahedra, the Mites__one
positive and one negative__may be
joined together to form the six-quanta-module, semisymmetrical,
allspace-filling Sytes.
The Mites can be assembled in three different ways to
produce three morphologically
different, allspace-filling, asymmetrical tetrahedra:
the Kites, Lites, and Bites, but all of the
same six-module volume. This is done in each by making
congruent matching sets of their
three, alternately matchable, right-triangle facets,
one of which is dissimilar to the other
two, while those other two are both positive-negative
mirror images of one another. Each
of the three pairings produces one six-quanta module
consisting of two A (+), two A (-),
one B (+), and one B (-).
|
|
|
953.50
Geometrical Combinations: All of the well-known Platonic,
Archimedean,
Keplerian, and Coxeter types of radially symmetric polyhedra
may be directly produced or
indirectly transformed from the whole unitary combining
of Mites without any
fractionation and in whole, rational number increments
of the A or B Quanta Module
volumes. This prospect may bring us within sight of
a plenitudinous complex of
conceptually discrete, energy-importing, -retaining,
and -exporting capabilities of nuclear
assemblage components, which has great significance
as a specific closed-system complex
with unique energy-behavior-elucidating phenomena. In
due course, its unique behaviors
may be identified with, and explain discretely, the
inventory of high-energy physics'
present prolific production of an equal variety of strange
small-energy "particles," which
are being brought into split-second existence and observation
by the ultrahigh-voltage
accelerator's bombardments.
|
|
|
953.60
Prime Minimum System: Since the asymmetrical tetrahedron
formed by
compounding two A Quanta Modules and one B Quanta Module,
the Mite, will compound
with multiples of itself to fill allspace and may be
turned inside out to form its
noncongruent negative complement, which may also be
compounded with multiples of
itself to fill allspace, this minimum asymmetric system__which
accommodates both
positive or negative space and whose volume is exactly
1/8th that of the tetrahedron,
exactly 1/32nd that of the octahedron, exactly 1/160th
that of the vector equilibrium of
zero frequency, and exactly 1/1280th of the vector equilibrium
of initial frequency ( = 2),
1280 = 28 × 5__this Mite constitutes the generalized
nuclear geometric limit of rational
differentiation and is most suitably to be identified
as the prime minimum system; it may
also be identified as the prime, minimum, rationally
volumed and rationally associable,
structural system.
|
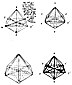 Fig. 954.00A 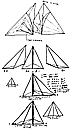 Fig. 954.00B |
954.00
Mite as the Coupler's Asymmetrical Octant Zone Filler
|
|
|
954.01
The Coupler is the asymmetric octahedron to be elucidated
in Secs.
954.20
through
954.70.
The Coupler has one of the most profound
integral functionings in
metaphysical Universe, and probably so in physical Universe,
because its integral
complexities consist entirely of integral rearrangeability
within the same space of the same
plus and/or minus Mites. We will now inspect the characteristics
and properties of those
Mites as they function in the Coupler. Three disparately
conformed, nonequitriangular,
polarized half-octahedra, each consisting of the same
four equivolumetric octant zones
occur around the three half-octants' common volumetric
center. These eight octant zones
are all occupied, in three possible different system
arrangements, by identical asymmetrical
tetrahedra, which are Mites, each consisting of the
three AAB Modules.
|
|
|
954.02
Each of these l/8 octant-zone-filling tetrahedral
Mite's respective surfaces
consists of four triangles, CAA, DEE, EFG1, and EFG2,
two of which, CAA and DBB,
are dissimilar isosceles triangles and two of which,
EFG1 and EFG2, are right triangles.
(See Illus.
953.10.)
Each of the dissimilar isosceles
triangles have one mutual edge, AA
and BB, which is the base respectively of both the isosceles
triangles whose respective
symmetrical apexes, C and D, are at different distances
from that mutual baseline.
|
|
|
954.03
The smaller of the mutually based isosceles triangle's
apex is a right angle,
D. If we consider the right-angle-apexed isosceles triangle
DBB to be the horizontal base
of a unique octant-zone-filling tetrahedron, we find
the sixth edge of the tetrahedron rising
perpendicularly from the right-angle apex, D, of the
base to C (FF), which perpendicular
produces two additional right triangles, FGE1 and FGE2,
vertically adjoining and thus
surrounding the isosceles base triangle's right-angled
apex, D. This perpendicular D (FF)
connects at its top with the apex C of the larger isosceles
triangle whose baseline, AA, is
symmetrically opposite that C apex and congruent with
the baseline, BB, of the right-
angle-apexed isosceles base triangle, BBD, of our unique
octant-filling tetrahedral Mite,
AACD.
|
|
|
954.04
The two vertical right triangles running between the
equilateral edges of the
large and small isosceles triangles are identical right
triangles, EFG1 and EFG2, whose
largest (top) angles are each 54° 44' and whose smaller
angles are 35° 16' each.
|
|
|
954.05
As a tetrahedron, the Mite has four triangular faces:
BBD, AAC, EFG1, and
EFG2. Two of the faces are dissimilar isosceles triangles,
BBD and AAC; ergo, they have
only two sets of two different face angles each__B, D,
A, and C__one of which, D, is a
right angle.
|
|
|
954.06
The other two tetrahedral faces of the Mites are similar
right triangles, EFG,
which introduce only two more unique angles, E and F,
to the Mite's surface inventory of
unique angles.
|
|
|
954.07
The inventory of the Mite's twelve corner angles reveals
only five different
angles. There are two As and two Fs, all of which are
54° 44' each, while there are three
right angles consisting of one D and two Gs. There are
two Bs of 45° 00' each, two Es of
35° 16' each, and one C of 70° 32'. (See drawings section.)
|
|
|
954.08
Any of these eight interior octant, double-isosceles,
three-right-angled-
tetrahedral domains__Mites__(which are so arrayed around
the center of volume of the
asymmetrical octahedron) can be either a positively
or a negatively composited allspace-
filling tetrahedron.
|
|
|
954.09
We find the Mite tetrahedron, AACD, to be the smallest,
simplest,
geometrically possible (volume, field, or charge), allspace-filling
module of the isotropic
vector matrix of Universe. Because it is a tetrahedron,
it also qualifies as a structural
system. Its volume is exactly l/8th that of its regular
tetrahedral counterpart in their
common magnitude isotropic vector matrix; within this
matrix, it is also only 1/24th the
volume of its corresponding allspace-filling cube, 1/48th
the volume of its corresponding
allspace-filling rhombic dodecahedron, and 1/6144th
the volume of its one other known
unique, omnidirectional, symmetrically aggregatable,
nonpolarized-assemblage, unit-
magnitude, isotropic-vector-matrix counterpart, the
allspace-filling tetrakaidecahedron.
|
|
|
954.10
Allspace-Filling Hierarchy as Rationally Quantifiable
in Whole Volume Units of A or B Quanta Modules
|
|
|
954.10A
Allspace-Filling Hierarchy as Rationally Quantifiable
in Whole Volume
Units of A or B Quanta Modules
|
|
|
954.20
Coupler: The basic complementarity of our octahedron
and tetrahedron,
which always share the disparate numbers 1 and 4 in
our topological analysis (despite its
being double or 4 in relation to tetra = 1), is explained
by the uniquely asymmetrical
octahedron, the Coupler, that is always constituted
by the many different admixtures of
AAB Quanta Modules; the Mites, the Sytes, the cube (72
As and Bs), and the rhombic
dodecahedron (144 As and Bs).
|
|
|
954.21
There are always 24 As or Bs in our uniquely asymmetrical
octahedron (the
same as one tetra), which we will name the Coupler because
it occurs between the
respective volumetric centers of any two of the adjacently
matching diamond faces of all
the symmetrical, allspace-filling rhombic dodecahedra
(or 144 As and Bs). The rhombic
dodecahedron is the most-faceted, identical-faceted
(diamond) polyhedron and accounts,
congruently and symmetrically, for all the unique domains
of all the isotropic-vector-
matrix vertexes. (Each of the isotropic-vector-matrix
vertexes is surrounded symmetrically
either by the spheres or the intervening spaces-between-spheres
of the closest-packed
sphere aggregates.) Each rhombic dodecahedron's diamond
face is at the long-axis center
of each Coupler (vol. = 1) asymmetric octahedron. Each
of the 12 rhombic dodecahedra is
completely and symmetrically omnisurrounded by__and diamond-face-bonded
with__12
other such rhombic dodecahedra, each representing one
closest-packed sphere and that
sphere's unique, cosmic, intersphere-space domain Lying
exactly between the center of the
nuclear rhombic dodecahedron and the centers of their
12 surrounding rhombic
dodecahedra__the Couplers of those closest-packed-sphere
domains having obviously
unique cosmic functioning.
|
|
|
954.22
A variety of energy effects of the A and B Quanta
Module associabilities are
contained uniquely and are properties of the Couplers,
one of whose unique characteristics
is that the Coupler's topological volume is the exact
prime number one of our synergetics'
tetrahedron (24 As) accounting system. It is the asymmetry
of the Bs (of identical volume
to the As) that provides the variety of other than plusness
and minusness of the all-A-
constellated tetrahedra. Now we see the octahedra that
are allspace filling and of the same
volume as the As in complementation. We see proton and
neutron complementation and
non-mirror-imaging interchangeability and intertransformability
with 24 subparticle
differentiabilities and 2, 3, 4, 6, combinations__enough
to account for all the isotopal
variations and all the nuclear substructurings in omnirational
quantation.
|
| Next Section: 954.30 |