
 Summary: Wave Propagation Model
Summary: Wave Propagation Model

|
905.70  Summary: Wave Propagation Model
Summary: Wave Propagation Model
|

|
905.71
 Both in the spherical vector equilibrium and in the
disequilibrious icosahedral
spherical system, the prime number five is produced
by the fundamental allspace-filling
complementarity of the l-volume tetrahedron and the
4-volume octahedron.
Both in the spherical vector equilibrium and in the
disequilibrious icosahedral
spherical system, the prime number five is produced
by the fundamental allspace-filling
complementarity of the l-volume tetrahedron and the
4-volume octahedron.
|

|
905.72
 We now understand how the equilibrious 48 basic triangles
transform into
the 120 disequilibrious basic triangles. The 120 (60
positive and 60 negative) LCD
spherical triangles' central (or nuclear) angles are
unaltered as we transform their eternal
systemic patterning symmetry from (a) the octahedral
form of l20/8=15 A Quanta
Modules per each octa triangle; to (b) the icosahedron's
120/20 = 6 A Quanta Modules
per each icosa triangle; to (c) the dodecahedron's l20/l2
= 10 A Quanta Modules per each
pentagon. This transformational progression demonstrates
the experientially witnessable,
wave-producing surface-askewing caused by the 120-degree,
alternating rotation of the
icosahedron's triangles inside of the octahedron's triangles.
Concomitant with this
alternating rotation we witness the shuttling of the
spherical vector equilibrium's 12
vertexial positions in a successive shifting-back-and-forth
between the spherical
icosahedron's 12 vertexial positions; as well as the
wave-propagating symmetrical,
polyhedral alterations of the inward-outward pulsations
which generate surface
undulations consequent to the radial contractions, at
any one time, of only a fractional
number of all the exterior vertexes, while a symmetrical
set of vertexes remains unaltered.
We now understand how the equilibrious 48 basic triangles
transform into
the 120 disequilibrious basic triangles. The 120 (60
positive and 60 negative) LCD
spherical triangles' central (or nuclear) angles are
unaltered as we transform their eternal
systemic patterning symmetry from (a) the octahedral
form of l20/8=15 A Quanta
Modules per each octa triangle; to (b) the icosahedron's
120/20 = 6 A Quanta Modules
per each icosa triangle; to (c) the dodecahedron's l20/l2
= 10 A Quanta Modules per each
pentagon. This transformational progression demonstrates
the experientially witnessable,
wave-producing surface-askewing caused by the 120-degree,
alternating rotation of the
icosahedron's triangles inside of the octahedron's triangles.
Concomitant with this
alternating rotation we witness the shuttling of the
spherical vector equilibrium's 12
vertexial positions in a successive shifting-back-and-forth
between the spherical
icosahedron's 12 vertexial positions; as well as the
wave-propagating symmetrical,
polyhedral alterations of the inward-outward pulsations
which generate surface
undulations consequent to the radial contractions, at
any one time, of only a fractional
number of all the exterior vertexes, while a symmetrical
set of vertexes remains unaltered.
|

|
905.73
 This elucidates the fundamental, electromagnetic,
inward-outward, and
complex great-circling-around type of wave propagation,
as does also the model of
spheres becoming voids and all the voids becoming spheres,
and their omniradiant wave
propagation (see Sec.
1032).
This elucidates the fundamental, electromagnetic,
inward-outward, and
complex great-circling-around type of wave propagation,
as does also the model of
spheres becoming voids and all the voids becoming spheres,
and their omniradiant wave
propagation (see Sec.
1032).
|

|
905.74
 There are also the approximately unlimited ranges
of frequency
modulatabilities occasioned by the symmetrical subdivisioning
of all the prime, equiangled,
surface triangles of the tetrahedron, octahedron, and
icosahedron. This additionally
permitted wave undulation of surface pattern shifting
is directly identified with the
appearance of photons as spherically clustered and radiantly
emittable tetrahedra (see Sec.
541.30).
There are also the approximately unlimited ranges
of frequency
modulatabilities occasioned by the symmetrical subdivisioning
of all the prime, equiangled,
surface triangles of the tetrahedron, octahedron, and
icosahedron. This additionally
permitted wave undulation of surface pattern shifting
is directly identified with the
appearance of photons as spherically clustered and radiantly
emittable tetrahedra (see Sec.
541.30).
|
910.00
 A and B Quanta Modules
A and B Quanta Modules

|
910.01
 All omni-closest-packed, complex, structural phenomena
are
omnisymmetrically componented only by tetrahedra and
octahedra. Icosahedra, though
symmetrical in themselves, will not close-pack with
one another or with any other
symmetrical polyhedra; icosahedra will, however, face-bond
together to form open-
network octahedra.
All omni-closest-packed, complex, structural phenomena
are
omnisymmetrically componented only by tetrahedra and
octahedra. Icosahedra, though
symmetrical in themselves, will not close-pack with
one another or with any other
symmetrical polyhedra; icosahedra will, however, face-bond
together to form open-
network octahedra.
|

|
910.02
 In an isotropic vector matrix, it will be discovered
that there are only two
omnisymmetrical polyhedra universally described by the
configuration of the interacting
vector lines: these two polyhedra are the regular tetrahedron
and the regular octahedron.
In an isotropic vector matrix, it will be discovered
that there are only two
omnisymmetrical polyhedra universally described by the
configuration of the interacting
vector lines: these two polyhedra are the regular tetrahedron
and the regular octahedron.
|

|
910.10
 Rational Fraction Elements
Rational Fraction Elements
|

|
910.11
 All other regular, omnisymmetric, uniform-edged, -angled,
and -faceted, as
well as several semisymmetric, and all other asymmetric
polyhedra other than the
icosahedron and the pentagonal dodecahedron, are described
repetitiously by
compounding rational fraction elements of the tetrahedron
and octahedron. These
elements are known in synergetics as the A and B Quanta
Modules. They each have a
volume of l/24th of a tetrahedron.
All other regular, omnisymmetric, uniform-edged, -angled,
and -faceted, as
well as several semisymmetric, and all other asymmetric
polyhedra other than the
icosahedron and the pentagonal dodecahedron, are described
repetitiously by
compounding rational fraction elements of the tetrahedron
and octahedron. These
elements are known in synergetics as the A and B Quanta
Modules. They each have a
volume of l/24th of a tetrahedron.
|

|
911.00
 Division of Tetrahedron
Division of Tetrahedron
|

|
911.01
 The regular tetrahedron may be divided volumetrically
into four identical
Quarter-Tetrahedra, with all their respective apexes
at the center of volume of the regular
unit tetrahedron. (See Illus.
913.01.) The Quarter-Tetrahedra
are irregular pyramids
formed upon each of the four triangular faces of the
original unit tetrahedra, with their
four interior apexes congruent at the regular tetrahedron's
volumetric center; and they
each have a volume of one quarter of the regular tetrahedron's
volume-1.
The regular tetrahedron may be divided volumetrically
into four identical
Quarter-Tetrahedra, with all their respective apexes
at the center of volume of the regular
unit tetrahedron. (See Illus.
913.01.) The Quarter-Tetrahedra
are irregular pyramids
formed upon each of the four triangular faces of the
original unit tetrahedra, with their
four interior apexes congruent at the regular tetrahedron's
volumetric center; and they
each have a volume of one quarter of the regular tetrahedron's
volume-1.
|

|
911.02
 Any of the Quarter-Tetrahedra may be further uniformly
subdivided into six
identical irregular tetrahedra by describing lines that
are perpendicular bisectors from each
vertex to their opposite edge of the Quarter-Tetrahedron.
The three perpendicular
bisectors cut each Quarter-Tetrahedron into six similar
tetrahedral pieces of pie. Each one
of the six uniformly symmetrical components must be
l/6th of One Quarter, which is l/24th
of a regular tetrahedron, which is the volume and description
of the A Quanta Module.
(See Illus.
913.01B.)
Any of the Quarter-Tetrahedra may be further uniformly
subdivided into six
identical irregular tetrahedra by describing lines that
are perpendicular bisectors from each
vertex to their opposite edge of the Quarter-Tetrahedron.
The three perpendicular
bisectors cut each Quarter-Tetrahedron into six similar
tetrahedral pieces of pie. Each one
of the six uniformly symmetrical components must be
l/6th of One Quarter, which is l/24th
of a regular tetrahedron, which is the volume and description
of the A Quanta Module.
(See Illus.
913.01B.)
|

|
912.00
 Division of Octahedron
Division of Octahedron
|

|
912.01
 The regular octahedron has a volume equivalent to
that of four unit
tetrahedra. The octahedron may be subdivided symmetrically
into eight equal parts, as
Eighth-Octahedra, by planes going through the three
axes connecting its six vertexes. (See
Illus.
916.01.)
The regular octahedron has a volume equivalent to
that of four unit
tetrahedra. The octahedron may be subdivided symmetrically
into eight equal parts, as
Eighth-Octahedra, by planes going through the three
axes connecting its six vertexes. (See
Illus.
916.01.)
|

|
912.02
 The Quarter-Tetrahedron and the Eighth-Octahedron
each have an
equilateral triangular base, and each of the base edges
is identical in length. With their
equiangular-triangle bases congruent we can superimpose
the Eighth-Octahedron over the
Quarter-Tetrahedron because the volume of the Eighth-Octahedron
is l/2 and the volume
of the Quarter-Tetrahedron is 1/4. The volume of the
Eighth-Octahedron is twice that of
the Quarter-Tetrahedron; therefore, the Eighth-Octahedron
must have twice the altitude
because it has the same base and its volume is twice
as great.
The Quarter-Tetrahedron and the Eighth-Octahedron
each have an
equilateral triangular base, and each of the base edges
is identical in length. With their
equiangular-triangle bases congruent we can superimpose
the Eighth-Octahedron over the
Quarter-Tetrahedron because the volume of the Eighth-Octahedron
is l/2 and the volume
of the Quarter-Tetrahedron is 1/4. The volume of the
Eighth-Octahedron is twice that of
the Quarter-Tetrahedron; therefore, the Eighth-Octahedron
must have twice the altitude
because it has the same base and its volume is twice
as great.
|

|
913.00
 A Quanta Module
A Quanta Module
|
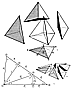 Fig. 913.01 |
913.01
 The A Quanta Module is l/6th of a Quarter-Tetrahedron.
The six
asymmetrical components of the Quarter-Tetrahedron each
have a volume of l/24th of the
unit tetrahedron. They are identical in volume and dimension,
but three of them are
positive and three of them are negative. (See Illus.
913.01.)
The A Quanta Module is l/6th of a Quarter-Tetrahedron.
The six
asymmetrical components of the Quarter-Tetrahedron each
have a volume of l/24th of the
unit tetrahedron. They are identical in volume and dimension,
but three of them are
positive and three of them are negative. (See Illus.
913.01.)
|

|
913.10
 Positive and Negative: The positive and negative A
Quanta Modules (the +
and the -) will not nest in one another congruently
despite identical angles, edges, and
faces. The pluses are inside-out minuses, which can
be shown by opening three of their six
edges and folding the three triangles' hinged edges
in the opposite direction until their
edges come together again.
Positive and Negative: The positive and negative A
Quanta Modules (the +
and the -) will not nest in one another congruently
despite identical angles, edges, and
faces. The pluses are inside-out minuses, which can
be shown by opening three of their six
edges and folding the three triangles' hinged edges
in the opposite direction until their
edges come together again.
|

|
913.11
 The A Quanta Module triangle is possibly a unique
scalene in that neither of
its two perpendiculars bisect the edges that they intersect.
It has three internal foldables
and no "internally contained" triangle. It drops its
perpendiculars in such a manner that
there are only three external edge increments, which
divide the perimeter into six
increments of three pairs.
The A Quanta Module triangle is possibly a unique
scalene in that neither of
its two perpendiculars bisect the edges that they intersect.
It has three internal foldables
and no "internally contained" triangle. It drops its
perpendiculars in such a manner that
there are only three external edge increments, which
divide the perimeter into six
increments of three pairs.
|

|
914.00
 A Quanta Module: Foldability
A Quanta Module: Foldability
|

|
914.01
 The A Quanta Module can be unfolded into a planar
triangle, an
asymmetrical triangle with three different edge sizes,
yet with the rare property of folding
up into a whole irregular tetrahedron.
The A Quanta Module can be unfolded into a planar
triangle, an
asymmetrical triangle with three different edge sizes,
yet with the rare property of folding
up into a whole irregular tetrahedron.
|

|
914.02
 An equilateral planar triangle AAA may be bisected
in each edge by points
BBB. The triangle AAA may be folded on lines BB, BB,
BB, and points A, A, A will
coincide to form the regular tetrahedron. This is very
well known.
An equilateral planar triangle AAA may be bisected
in each edge by points
BBB. The triangle AAA may be folded on lines BB, BB,
BB, and points A, A, A will
coincide to form the regular tetrahedron. This is very
well known.
|

|
914.10
 Four Right Angles: In respect to the A Quanta Module
flatout triangle or
infolded to form the irregular tetrahedron, we find
by the method of the module's
construction (by perpendicular planes carving apart)
that there are four right angles (see
Illus.
913.01C):
Four Right Angles: In respect to the A Quanta Module
flatout triangle or
infolded to form the irregular tetrahedron, we find
by the method of the module's
construction (by perpendicular planes carving apart)
that there are four right angles (see
Illus.
913.01C):
|

|
914.20
 Unfolding into a Flat Triangle: If we go to the vertex
at E and break open
the edges ED and AD, we can hinge open triangle EBF
on hinge line EF. We can then
break open the edge AC and fold triangle ADC, as well
as folding out the two triangles
DEC and CEF, which are connected by the hinge EC, so
that now the whole asymmetric
A Quanta Module is stretched out flat as a triangle.
Unfolding into a Flat Triangle: If we go to the vertex
at E and break open
the edges ED and AD, we can hinge open triangle EBF
on hinge line EF. We can then
break open the edge AC and fold triangle ADC, as well
as folding out the two triangles
DEC and CEF, which are connected by the hinge EC, so
that now the whole asymmetric
A Quanta Module is stretched out flat as a triangle.
|

|
914.21
 The A Quanta Module unfolds into a scalene triangle;
that is, all of its non-
degree angles are different, and all are less than
90 degrees. Two of the folds are
perpendicular to the triangle's sides, thus producing
the four right angles. The A Quanta
Module triangle may be the only triangle fulfilling
all the above stated conditions.
The A Quanta Module unfolds into a scalene triangle;
that is, all of its non-
degree angles are different, and all are less than
90 degrees. Two of the folds are
perpendicular to the triangle's sides, thus producing
the four right angles. The A Quanta
Module triangle may be the only triangle fulfilling
all the above stated conditions.
|

|
914.30
 Spiral Foldability: The foldability of the A Quanta
Module planar triangle
differs from the inter-mid-edge foldability of the equilateral
or isosceles triangle. All the
mid-edge-foldable equilateral or isosceles triangles
can all form tetrahedra, regular or
irregular. In the case of the folded equilateral or
isosceles triangle, the three triangle
corners meet together at one vertex: like petals of
a flower. In the case of the inter-mid-
edge-folding scalene triangle, the three corners fail
to meet at one vertex to form a
tetrahedron.
Spiral Foldability: The foldability of the A Quanta
Module planar triangle
differs from the inter-mid-edge foldability of the equilateral
or isosceles triangle. All the
mid-edge-foldable equilateral or isosceles triangles
can all form tetrahedra, regular or
irregular. In the case of the folded equilateral or
isosceles triangle, the three triangle
corners meet together at one vertex: like petals of
a flower. In the case of the inter-mid-
edge-folding scalene triangle, the three corners fail
to meet at one vertex to form a
tetrahedron.
|

|
915.00
 Twinkle Angle
Twinkle Angle
|

|
915.01
 The faces of an A Quanta Module unfold to form a triangle
with 84° 44' (30°
00' + 35° 16' + 19° 28') as its largest angle. This is
5° 16' less than a right angle, and is
known as the twinkle angle in synergetics (see Illus.
913.01C).
The faces of an A Quanta Module unfold to form a triangle
with 84° 44' (30°
00' + 35° 16' + 19° 28') as its largest angle. This is
5° 16' less than a right angle, and is
known as the twinkle angle in synergetics (see Illus.
913.01C).
|

|
915.02
 There is a unique 5° 16'-ness relationship of the A
Quanta Module to the
symmetry of the tetrahedron-octahedron allspace-filling
complementation and other
aspects of the vector equilibrium that is seemingly
out of gear with the disequilibrious
icosahedron. It has a plus-or-minus incrementation quality
in relation to the angular laws
common to the vector equilibrium.
There is a unique 5° 16'-ness relationship of the A
Quanta Module to the
symmetry of the tetrahedron-octahedron allspace-filling
complementation and other
aspects of the vector equilibrium that is seemingly
out of gear with the disequilibrious
icosahedron. It has a plus-or-minus incrementation quality
in relation to the angular laws
common to the vector equilibrium.
|

|
915.10
 A Quanta Module Triangle and Basic Disequilibrium
120 LCD
Triangle: The angles of fold of the A Quanta Module
triangle correspond in patterning to
the angles of fold of the Basic Disequilibrium 120 LCD
Triangle, the 1/120th of a sphere
whose fundamental great circles of basic symmetry subdivide
it in the same way. The
angles are the same proportionally when the spherical
excess subsides proportionally in all
three corners. For instance, the angle ACB in Illus.
913.01C
is not 90 degrees, but a little
less.
A Quanta Module Triangle and Basic Disequilibrium
120 LCD
Triangle: The angles of fold of the A Quanta Module
triangle correspond in patterning to
the angles of fold of the Basic Disequilibrium 120 LCD
Triangle, the 1/120th of a sphere
whose fundamental great circles of basic symmetry subdivide
it in the same way. The
angles are the same proportionally when the spherical
excess subsides proportionally in all
three corners. For instance, the angle ACB in Illus.
913.01C
is not 90 degrees, but a little
less.
|

|
915.11
 It is probable that these two closely akin triangles
and their respective folded
tetrahedra, whose A Module Quantum phase is a rational
subdivider function of all the
hierarchy of atomic triangulated substructuring, the
120 Basic Disequilibrium LCD
triangles and the A Module triangles, are the same quanta
reoccurrent in their most
powerful wave-angle oscillating, intertransformable
extremes.
It is probable that these two closely akin triangles
and their respective folded
tetrahedra, whose A Module Quantum phase is a rational
subdivider function of all the
hierarchy of atomic triangulated substructuring, the
120 Basic Disequilibrium LCD
triangles and the A Module triangles, are the same quanta
reoccurrent in their most
powerful wave-angle oscillating, intertransformable
extremes.
|

|
915.20
 Probability of Equimagnitude Phases: The 6° spherical
excess of the
Basic Disequilibrium 120 LCD Triangle, the 5° 16' "twinkle
angle" of the A Quanta
Module triangle, and the 7° 20' "unzipping angle" of
birth, as in the DNA tetrahelix,
together may in time disclose many equimagnitude phases
occurring between
complementary intertransforming structures.
Probability of Equimagnitude Phases: The 6° spherical
excess of the
Basic Disequilibrium 120 LCD Triangle, the 5° 16' "twinkle
angle" of the A Quanta
Module triangle, and the 7° 20' "unzipping angle" of
birth, as in the DNA tetrahelix,
together may in time disclose many equimagnitude phases
occurring between
complementary intertransforming structures.
|

|
916.00
 B Quanta Module
B Quanta Module
|
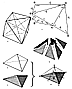 Fig. 916.01 |
916.01
 The B Quanta Module is 1/6th of the fractional unit
described by subtracting
a Quarter-Tetrahedron from an Eighth-Octahedron. The
six asymmetrical components of
the fractional unit so described each have a volume
of 1/24th of the unit tetrahedron. They
are identical in volume and dimensioning, but three
of them are positive and three of them
are negative. (See Illus.
916.01.)
The B Quanta Module is 1/6th of the fractional unit
described by subtracting
a Quarter-Tetrahedron from an Eighth-Octahedron. The
six asymmetrical components of
the fractional unit so described each have a volume
of 1/24th of the unit tetrahedron. They
are identical in volume and dimensioning, but three
of them are positive and three of them
are negative. (See Illus.
916.01.)
|

|
916.02
 When the Eighth-Octahedron is superimposed on the
Quarter-Tetrahedron,
the top half of the Eighth-Octahedron is a fractional
unit, like a concave lid, with a volume
and weight equal to that of the Quarter-Tetrahedron
below it. We can slice the fractional
unit by three planes perpendicular to its equilateral
triangular base and passing through the
apex of the Quarter-Tetrahedron, through the vertexes
of the triangular base, and through
the mid-points of their respective opposite edges, separating
it into six equidimensional,
equivolume parts. These are B Quanta Modules.
When the Eighth-Octahedron is superimposed on the
Quarter-Tetrahedron,
the top half of the Eighth-Octahedron is a fractional
unit, like a concave lid, with a volume
and weight equal to that of the Quarter-Tetrahedron
below it. We can slice the fractional
unit by three planes perpendicular to its equilateral
triangular base and passing through the
apex of the Quarter-Tetrahedron, through the vertexes
of the triangular base, and through
the mid-points of their respective opposite edges, separating
it into six equidimensional,
equivolume parts. These are B Quanta Modules.
|

|
916.03
 B Quanta Modules are identical irregular tetrahedra
that appear as three
positive (outside-out) and three negative (outside-in)
units. Each of the B Quanta Modules
can be unfolded into a planar, multitriangled polygon.
(See Illus.
916.01F.)
B Quanta Modules are identical irregular tetrahedra
that appear as three
positive (outside-out) and three negative (outside-in)
units. Each of the B Quanta Modules
can be unfolded into a planar, multitriangled polygon.
(See Illus.
916.01F.)
|
| Next Section: 920.00 |