986.090 The Search for Nature's Coordinate System
986.091 Several things were certain: nature is capable of both omnidirectional disorderly, dispersive, and destructive expansion and omnidirectional collective, selective sorting and constructive contraction; and rays of candlelight are not parallel to one another. I decided to initiate my search for nature's coordinate system by assuming that the coordinate system must be convergently and divergently interaccommodative. That the seasons of my New England childhood brought forth spectacular transformations in nature's total interpatterning; that the transformations were not simultaneous nor everywhere the same; that there were shaded and Sun-shined-upon area variables; and that they were all embraced by a comprehensive coordination__altogether made me dream of comprehending the comprehensively accommodating coordinate system that had no separate departments of chemistry, physics, biology, mathematics, art, history, or languages. I said nature has only one department and only one language.
986.092 These thoughts kept stimulating my explorations for the totally accommodative coordinate system. Einstein's conclusion-that the definitive, maximum possible speed of light rendered astronomical phenomena an aggregate of nonsimultaneous and only partially overlapping, differently enduring energy events__greatly affected the increasing inventory of my tentative formulations of the interaccommodative requirements of the cosmic coordination system which I sought. I was driven by both consciously and subconsciously sustained intuition and excitement. This was very private, however. I talked to no one about it. It was all very remote from that which seemed to characterize popular interest.
986.093 The youthful accruals of these long-sustained private observations, cogitations, and speculations were enormously helpful when I decided at the age of 32, in my crisis year of 1927, to abandon the game of competitive survival (a game I had been taught to believe in as thought-out, managed, and evolved entirely by others) and instead to rely completely upon my own thinking and experience-suggested inclinations . . . to find out how Universe is organized and what it is doing unbeknownst to humans. Why are humans here in Universe? What should we be doing to fulfill our designed functioning in Universe? Surely all those stars and galaxies were not designed only to be romantic scenery for human moods. What am I designed to be able to comprehend about Universe? What are we humans designed to be able to do for one another and for our Universe?
986.094 Expanding Universe: My determination to commit myself completely to the search for nature's raison d'ˆtre and for its comprehensive coordinate system's mathematics was greatly reinforced by the major discovery of the astronomer E. P. Hubble in 1924. He discovered an expanding macrocosmic system with all the myriads of galaxies and their respective stellar components at all times maintaining the same interangular orientations and relative interdistancings from one another while sum-totally and omnisymmetrically expanding and moving individually away from one another, and doing so at astronomical speeds. This discovery of Hubble's became known as Expanding Universe.
986.095 The only way humans can expand their houses is by constructing lopsided additions to their rectilinearly calculated contriving. People found that they could "blow up" rubber-balloon spheres to increase their radii, but they couldn't blow up their buildings except by dynamite. They called their wooden "2 × 4," and "2 × 6," and "2 × 8- inch" cross-section, wooden-timber nail-ups "balloon framing," but why they selected that name was difficult to explain.

Fig. 986.096 		986.096 My insights regarding nature's coordinate system were greatly enhanced by two of Milton Academy's greatest teachers: Homer LeSourd in physics and William Lusk Webster Field ("Biology Bill") in biology. During the summer vacation of 1906, at 11 years of age I designed and built my first small but exciting experimental dwelling on our family's small mid-Penobscot Bay island. Living all my youthful summers on that island, with its essential boat-building, boat-modifying, boat-upkeep, and boat-sailing, followed by five years as a line officer in the regular U.S. Navy with some of my own smaller-craft commands, some deck-officering on large craft of the new era's advanced technology ships, together with service involving airplanes, submarines, celestial navigation, ballistics, radio, and radiotelephone; then resignation from the Navy followed by five more private- enterprise years developing a new building system, inventing and installing its production tools, managing the production of the materials, and erecting therewith 240 residences and small commercial buildings__altogether finally transformed my sustained activity into full preoccupation with my early-boyhood determination some day to comprehend and codify nature's omniintertransformative, omnidirectional, cosmic coordination system and its holistic, only-experientially-proven mathematics. In 1928, inspired and fortified by Hubble's Expanding Universe discovery, I gave the name and its symbol 4-D to my mathematical preoccupations and their progressively discovered system codifying. In 1936 I renamed my discipline "Energetic Vectorial Geometry." In 1938 I again renamed it "Energetic-synergetic Geometry," and in 1970 for verbal economy contracted that title to "Synergetics." (See Fig. 986.096.)
986.100 Sequence of Considerations
986.101 At the outset of my lifelong search for nature's omnirational coordination system of mathematical interaccounting and intertransformability I proceeded through a sequence of considerations which may be enumerated as follows:
986.110 Consideration 1: Energetic Vectors
986.111 I first determined to employ only vectors for lines. I realized that operationally all lines are always trajectories of energy events, either as the energy invested by humans in the work of carving or depositing linearly__which we call "drawing" a line__or as the inanimately articulated energy of force lines.
986.112 Vectors always represent energy forces of given magnitude operating at given angles upon given entities at given loci, and vectors may always be demonstrated by lines representing given mass moving at given velocity in unique angular direction in respect to a given axis of observation. Vectors do not occur singly: They occur only as the total family of forces interacting in any given physical circumstance.
986.113 Vectors always have unique length, that length being the product of the mass and the velocity as expressed in a given modular system of measurement. Vectors do not have inherent extendibility to infinity__as did the lines of my boyhood's schoolteachers. Vectors are inherently terminal. Vectors bring into geometry all the qualities of energetic reality lacking in Euclidean geometry: time and energy-energy differentially divergent as radiation (velocity) and energy integratively convergent as matter (mass). Velocity and mass could be resolved into numerically described time and temperature components.
986.120 Consideration 2: Avogadro's Constant Energy Accounting
986.121 Avogadro discovered that under identical conditions of pressure and heat all elements in their gaseous state always consist of the same number of molecules per given volume. Since the chemical elements are fundamentally different in electron-proton componentation, this concept seemed to me to be the "Grand Central Station" of nature's numerical coordinate system's geometric volume-that numerically exact volumes contain constant, exact numbers of fundamental energy entities. This was the numerical and geometrical constancy for which I was looking. I determined to generalize Avogadro's experimentally proven hypothesis that "under identical conditions of heat and pressure all gases disclose the same number of molecules per given volume." (See Secs. 410.03-04.)
986.122 Here were Physical Universe's natural number quantations being constantly related to given volumes. Volumes are geometrical entities. Geometrically defined and calculated volumes are polyhedral systems. Polyhedra are defined by edge lines, each of which must be a vector.
986.123 Within any given volumetrically contained gaseous state the energy kinetics of molecules are everywhere the same. The outward pressure of air against the enclosing tube wall and casing of any one automobile tire is everywhere the same. Pressure and heat differentials involve isolated conditions__isolated by containers; ergo, special cases. To me this meant that we could further generalize Avogadro by saying that "`under identical, uncontained, freely self-interarranging conditions of energy all chemical elements will disclose the same number of fundamental somethings per given volume." This constant- volume-population-and-omniequilibrious-energy relationship would require physically demonstrable, substantive, geometrical combining of a given number of unique energetic- event entities per unit volume with constant-angularly-defined positional orientation integrities. This meant that the vectorially structured shapes of the volumes accommodating given numbers of most primitive energy events must be experientially demonstrable.
986.130 Consideration 3: Angular Constancy
986.131 I said that since vectors are physically modelable structural components, they produce conceptual structural models of energy events, and since my hypothetical generalization of Avogadro's law requires that "all the conditions of energy be everywhere the same," what does this condition look like as structured in vectorial geometry? Obviously all the vectors must be the same length and all of them must interact at the same angles. I said: It will make no difference what length is employed so long as they are all the same length. Linear size is special case. Special case occurs only in time. Angles are cosmically constant independently of time-size considerations.
986.140 Consideration 4: Isotropic Vector Model
986.141 I said, Can you make a vector model of this generalization of Avogadro? And I found that I had already done so in that kindergarten event in 1899 when I was almost inoperative visually and was exploring tactilely for a structural form that would hold its shape. This I could clearly feel was the triangle__with which I could make systems having insides and outsides. This was when I first made the octet truss out of toothpicks and semidried peas, which interstructuring pattern scientists decades later called the "isotropic vector matrix," meaning that the vectorial lengths and interanglings are everywhere the same. (See Sec. 410.06.)
986.142 This matrix was vectorially modelable since its lines, being vectors, did not lead to infinity. This isotropic vector matrix consists of six-edged tetrahedra plus 12-edged octahedra__multiples of six. Here is an uncontained omniequilibrious condition that not only could be, but spontaneously would be, reverted to anywhen and anywhere as a six- dimensional frame of transformative-evolution reference, and its vector lengths could be discretely tuned by uniform modular subdivisioning to accommodate any desired special case wavelength time-size, most economically interrelated, transmission or reception of physically describable information. (Compare Secs. 639.02 and 1075.10.)
986.143 Since the vectors are all identical in length, their intersection vertexes become the nuclear centers of unit-radius spheres in closest-packed aggregation__which closest packing is manifest by atoms in their crystal growth. All the foregoing brought the adoption of my vectorial geometry's everywhere-the-same (isotropic) vector matrix as the unified field capable of accommodating all of Physical Universe's intertransformative requirements.
986.150 Consideration 5: Closest Packing of Spheres
986.151 I had thus identified the isotropic vector matrix with the uniform linear distances between the centers of unit radius spheres, which aggregates became known later__in 1922__as "closest-packed" unit-radius spheres (Sec. 410.07 ), a condition within which we always have the same optimum number of the same "somethings"__spheres or maybe atoms__per given volume, and an optimally most stable and efficient aggregating arrangement known for past centuries by stackers of unit-radius coconuts or cannonballs and used by nature for all time in the closest packing of unit-radius atoms in crystals.
986.160 Consideration 6: Diametric Unity

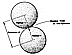Fig. 986.161 		986.161 The installation of the closest-packed unit-radius spheres into their geometrical congruence with the isotropic vector matrix showed that each of the vectors always reaches between the spheric centers of any two tangentially adjacent spheres. This meant that the radius of each of the kissing spheres consists of one-half of the interconnecting vectors. Wherefore, the radius of our closest-packed spheres being half of the system vector, it became obvious that if we wished to consider the radius of the unit sphere as unity, we must assume that the value of the vector inherently interconnecting two unit spheres is two. Unity is plural and at minimum two. Diameter means dia- meter__unit of system measurement is two.
986.162 Fig. 986.161 shows one vector D whose primitive value is two. Vectors are energy relationships. The phenomenon relationship exists at minimum between two entities, and the word unity means union, which is inherently at minimum two. "Unity is plural and at minimum two" also at the outset became a prime concept of synergetics vectorial geometry. (See Sec. 540.10.)
986.163 l R + l R = 2 R
2 R = Diameter
Diameter is the relative-conceptual-size determinant of a system. A diameter is the prime characteristic of the symmetrical system. The separate single system = unity. Diameter describes unity. Unity = 2. (See Secs. 905.10 and 1013.10.)
986.164 One by itself is nonexistent. Existence begins with awareness. Awareness begins with observable otherness. (See Secs. 264 and 981.)
986.165 Understanding means comprehending the interrelationship of the observer and the observed. Definitive understanding of interrelationships is expressed by ratios.
986.166 At the outset of my explorations I made the working assumption that unity is two, as combined with the experimentally demonstrable fact that every system and every systemic special case sphere is at once both a concave and a convex sphere__ergo, always inherently two spheres. Reflective concave surfaces convergently concentrate all impinging radiation, and reflective convex surfaces divergently diffuse all impinging radiation. Though concave and convex are inherently congruent as they are always-and- only coexisting, they are also diametrically opposed physical behavior phenomena__ergo, absolutely different because the one diffuses the energies of Universe, producing macrocosmic dispersion, and the other concentrates the energies of Universe, producing microcosmic convergence. Concave and convex are explicitly two opposites cosituate (congruent) geometrically as one. This led me to the working assumption at the outset of my__thus far__60-year exploration for nature's own coordinate system, that unity is inherently plural and at minimum is to be dealt with as the value two, which twoness might well coexist with other numbers of inherent properties of primary-existence systems.
986.170 Consideration 7: Vector Equilibrium
986.171 I then identified this closest-packed-spheres isotropic vector matrix as a generalized field condition of the everywhere-and-everywhen most economically interaccommodating of any plurality of nuclearly convergent-divergent, importively organizing, and exportingly info-dispensing energy events__while also providing for any number of individually discrete, overlappingly co-occurrent, frequency differentiated info- interexchangings__ergo, to be always accommodative of any number of co-occurrent, individual-pattern-integrity evolutionary scenarios.
986.172 Thus the eternally regenerative Universe, embracing the minimum complex of intercomplementary transformations necessary to effect total regeneration, becomes comprehensively accommodated by the only generalizably definable Scenario Universe as the condition of the vector equilibrium, an everywhere-everywhen condition at which nature refuses to pause, but through which most economically accommodating field of operational reference she pulsates her complex myriads of overlapping, concurrent, local intertransformings and aberrative structurings. I then invented the symbol 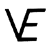to identify vector equilibrium.
986.180 Consideration 8: Concentric Polyhedral Hierarchy
986.181 Thereafter I set about sorting out the relative numbers and volumes of the most primitive hierarchy of symmetrically structured polyhedral-event "somethings"__all of which are always concentrically congruent and each and all of which are to be discovered as vertexially defined and structurally coexistent within the pre-time-size, pre- frequency-modulated isotropic vector matrix. (See Sec. and Fig. 982.61.)
986.190 Consideration 9: Synergetics
986.191 This book Synergetics (volumes 1 and 2) embraces the record of the lifetime search, research, sorting-outs, and structural-intertransforming experiments based upon the foregoing eight considerations, all of which I had adopted by 1927. This 1927 inventory has been progressively amplified by subsequent experience-induced considerations.
Next Section: 986.200
Copyright © 1997 Estate of R. Buckminster Fuller