Equilibrium and Disequilibrium Modelability
905.00
Equilibrium and Disequilibrium Modelability
|
905.01
Tetrahedron as Model: Synergetics is the geometry
of thinking. How we
think is epistemology, and epistemology is modelable;
which is to say that knowledge
organizes itself geometrically, i.e., with models.
|
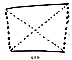 Fig. 905.02 |
905.02
Unity as two is inherent in life and the resulting
model is tetrahedral, the
conceptuality of which derives as follows:
|
|
|
905.10
Doubleness of Unity
|
|
|
905.11
The prime number twoness of the octahedron always
occurs in structuring
doubled together as four__i.e., 22 __a fourness which
is also doubleness of unity. Unity is
plural and, at minimum, is two. The unity volume 1 of
the tetrahedron is, in structural
verity, two, being both the outwardly displayed convex
tetrahedron and the inwardly
contained concave tetrahedron. (See Chart
223.64
, columns
2, 12, and 15)
|
|
|
905.12
The three-great-circle model of the spherical octahedron
only "seems" to be
three; it is in fact "double"; it is only foldably produceable
in unbroken (whole) great-circle
sheets by edge-combining six hemicircularly folded whole
great circles (see Sec.
840
).
Thus it is seen that the octahedron__as in Iceland spar
crystals__occurs only doubly, i.e.,
omnicongruent with itself, which is "quadrivalent."
|
|
|
905.13
Among the three possible omnisymmetrical prime structural
systems__the
tetrahedron, octahedron, and icosahedron__only the tetrahedron
has each of its vertexes
diametrically opposite a triangular opening. (See Illus.
610.2.)
In the octahedron and
icosahedron, each vertex is opposite another vertex;
and each of their vertexes is
diametrically blocked against articulating a self-inside-outing
transformation. In both the
octahedron and the icosahedron, each of the vertexes
is tense-vector-restrained from
escaping outwardly by the convergent vectorial strength
of the system's other immediately
surrounding__at minimum three__vertexial event neighbors.
But contrariwise, each of the
octahedron's and icosahedron's vertex events are constrainingly
impulsed inwardly in an
exact central-system direction and thence impelled toward
diametric exit and inside-outing
transformation; and their vertex events would do so
were it not for their diametrically
opposed vertexes, which are surroundingly tense-vector-restrained
from permitting such
outward egress.
|
|
|
905.14
As a consequence of its uniquely unopposed diametric
vertexing__ergo
permitted__diametric exit, only the tetrahedron among
all the symmetric polyhedra can
turn itself pulsatingly inside-out, and can do so in
eight different ways (see Sec.
624
); and
in each instance, as it does so, one-half of its combined
concave-convex unity "twoness" is
always inherently invisible.
|
|
|
905.15
The octahedron, however, restrainingly vector-blocked
as described, can
only infold itself pulsatingly to a condition of hemispherical
congruence like a deflated
basketball. Thus the octahedron's concave-convex, unity-twoness
state remains plurally
obvious. You can see the concave infolded hemisphere
nested into the as-yet outfolded
convex hemisphere. Verifying the octahedron's fourness
as being an evolutionary
transformation of the tetrahedron's unity-twoness, we
may take the four triangles of the
tetrahedron which were edge-hinged together (bivalently)
and reassemble them univalently
(that is, corner-to-corner) and produce the octahedron,
four of whose faces are triangular
(ergo structurally stable) voids. This, incidentally,
introduces the structural stability of the
triangle as a visualizable yet physical nothingness.
|
|
|
905.16
The triangle is structure. Structure is spontaneous
pattern stabilization of a
complex of six individual events. Structure is an integral
of six events. Structure is a
pattern integrity. Pattern integrity is conceptual relationship
independent of size. The
integrity of the nuclear structuring of the atoms is
conceptually thinkable, as are the
associability and disassociability proclivities of chemistry,
virology, biology, and all
nonbiological structuring and mechanics.
|
|
|
905.17
Any and all of the icosahedron's vertexes pulsate
individually and
independently from the convex to concave state only
in the form of local dimpling,
because each only-from-outward-motion-restrained vertex__being
free to articulate
inwardly toward its system center, and having done so__becomes
abruptly five-vector-
restrained by its immediate neighboring vertexial event
convergences; and the abrupt
halting of its inward travel occurs before it reaches
the system center. This means that one
vertex cannot pulse inwardly more deeply than a local
dimple similar to the popping in of a
derby hat. (See Sec.
618.30
.)
|
|
|
905.18
Both the coexisting concave and convex aspects of
the icosahedron__like
those of the octahedron, but unlike those of the unique
case of the tetrahedron__are
always visually obvious on the inside and outside of
the only locally dimpled-in, or nested-
in, vertex. In both the octahedron and the icosahedron,
the concave-convex, only inwardly
pulsative self-transforming always produces visually
asymmetrical transforming; whereas
the tetrahedron's permitted inside-outing pulsatively
results only in a visible symmetry, the
quasiasymmetry being invisibly polarized with the remainder
of Universe outside the
tetrahedron, which, being omniradially outward,
is inferentially__but not
visually__symmetrical; the only asymmetrical consideration
of the tetrahedron's inside-
outing being that of an initial direction of vertexial
exiting. Once exited, the visible
remaining symmetrical tetrahedron is in verity the inside-outness
of its previously visible
aspects. (See Sec.
232.01
.)
|
|
|
905.19
In either of the two sets of four each as alternatively
described, one of the
polar states is always visible and the other complementarily
invisible. This is a dynamic
relationship. Dynamically, all four of each of the two
sets of the tetrahedral potential are
co-occurrently permitted and are required by omni-action-reaction-resultant
synergetics.
The seeming significance of the separately considered
asymmetries are cancelled by the
omnidirectional symmetry.
|
|
|
905.20
The vertexes are the unique, individual, ergo in-time
events; and the
nonvertex voids are the outdividual, ergo out, timeless,
sizeless nonevents. The both
outwardly and inwardly escaping nonevents complement
the embryo, local-in-time,
special-case, convergent-event, systemic pattern fixation
of individual intercomplementary
event identities. (See Sec.
524
.)
|
|
|
905.21
In is unidirectional, pointable. Out is omnidirectional,
unpointable__go out,
to-go-out, or go-in-to-go-out on the other side. Any
direction from here is out; only one
direction from here is in. Go either temporarily in
to go diametrically out on the other side
of the individually identical local in, or go anydirectionally
out . . . to the complete,
eternal, unidentifiable, nonness, noneness of the a
priori mysterious, integrally
regenerative, inherently complex Universe.
|
|
|
905.22
So-called edges and vectors are inherently only convergent
or divergent
interrelationships between multiply-identifiable, point-to-able,
vertex fixes.
|
|
|
905.23
Because each tetrahedron has both four vertexes and
four subtending
nonvertex voids, we can identify those four diametrically
complementary sets of all
minimal cosmic structural systems as the four visible
vertexes and the four nonvisible
nonvertexes, i.e., the triangularly symmetrical, peripheral
voids. The tetrahedron thus
introduces experientially the cosmic principle of the
visible and invisible pairs or couples;
with the nonvisible vertex as the inside-out vertex,
which nonvertex is a nonconvergence
of events; whereas the vertexes are visible event convergences.
|
|
|
905.30
Hierarchy of Pulsating Tetrahedral Arrays
|
|
|
905.31
Among the exclusively, three and only, prime cosmic
structural systems__the
tetra, octa, and icosa__only the tetrahedron's pulsative
transforming does not alter its
overall, visually witnessable symmetry, as in the case
of the "cheese tetrahedron" (see Sec.
623.00).
It is important to comprehend that any one of
the two sets of four each potential
vertexial inside-outing pulsatabilities of the tetrahedron__considered
only by
themselves__constitutes polarized, but only invisible,
asymmetry. In one of the two sets of
four each potential inside-outings we have three-of-each-to-three-of-the-other
(i.e.,
trivalent, triangular, base-to-base) vertexial bonding
together of the visible and invisible,
polarized pair of tetrahedra. In the other of the two
sets of four each potential inside-
outings we have one-vertex-to-one-vertex (i.e., univalent,
apex-to-apex) interbonding of
the visible and invisible polarized pair of tetrahedra.
|
|
|
905.32
Because each simplest, ergo prime, structural system
tetrahedron has at
minimum four vertexes (point-to-able, systemic, event-patterned
fixes), and their four
complementary system exit-outs, are symmetrically identified
at mid-void equidistance
between the three other convergent event identity vertexes;
and because each of the two
sets of these four half-visible/half-invisible, polar-paired
tetrahedra have both three-vertex-
to-three-vertex as well as single-vertex-to-single-vertex
inside-out pulsatabilities; there are
eight possible inside-outing pulsatabilities. We have
learned (see Sec.
440
) that the vector
equilibrium is the nuclear-embracing phase of all eight
"empty state" tetrahedra, all with
common, central, single-vertex-to-single-vertex congruency,
as well as with their mutual
outward-radius-ends' vertexial congruency; ergo the
vector equilibrium is bivalent.
|
|
|
905.33
The same vector equilibrium's eight, nuclear-embracing,
bivalent
tetrahedra's eight nuclear congruent vertexes may be
simultaneously outwardly pulsed
through their radially-opposite, outward, triangular
exits to form eight externally pointing
tetrahedra, which thus become only univalently, i.e.,
only-single-vertex interlinked, and
altogether symmetrically arrayed around the vector equilibrium's
eight outward "faces."
The thus formed, eight-pointed star system consisting
of the vector equilibrium's volume
of 20 (tetrahedral unity), plus the eight star-point-arrayed
tetrahedra, total volumetrically
to 28. This number, 28, introduces the prime number
seven factored exclusively with the
prime number two, as already discovered in the unity-twoness
of the tetrahedron's always
and only, co-occurring, concave-convex inherently disparate,
behavioral duality. This
phenomenon may be compared with the 28-ness in the Coupler
accounting (see Sec.
954.72).
|
|
|
905.34
We have also learned in the vector equilibrium jitterbugging
that the vector
equilibrium contracts symmetrically into the octahedral
state, and we thus witness in the
octahedron the eight tetrahedra__three-vertex-to-three-vertex
(face-to-face, trivalent,
triple-interbonded)__which condition elucidates the octahedron's
having a volumetric four
in respect to the tetrahedron's dual unity. Whereas
the octahedron's prime number is two
in respect to the tetrahedron's prime number one, it
is experientially evidenced that the
octahedron always occurs as both the double phase and
the fourfold phase of the
tetrahedron; i.e., as (a) the tetrahedral invisible/visible,
(No-Yes), concave/convex; as well
as (b) the octahedral visible/visible, (Yes-Yes), concave/convex:
two different twoness
manifestations. The tetrahedron has a unity-two duality
in both its generalized dynamic
potential and kinetic states, having always both the
cosmic macro-tetrahedron and the
cosmic micro-tetrahedron, both embracingly and inclusively
defined by the four
convergent event fixes of the minimum structural system
of Universe. There is also the
fundamental twoness of the tetrahedron's three sets
of two-each, opposed, 90-degree-
oriented edgevectors whose respective four ends are
always most economically omni-
interconnected by the four other vectors of the tetrahedron's
total of six edge-vectors.
|
|
|
905.35
The jitterbug shows that the bivalent vector equilibrium
contracts to the
octahedral trivalent phase, going from a twentyness
of volume to a fourness of volume,
20 4, i.e.,
a 5:1 contraction, which introduces the
prime number five into the exclusively
tetrahedrally evolved prime structural system intertransformabilities.
We also witness that
the octahedron state of the jitterbug transforms contractively
even further with the 60-
degree rotation of one of its triangular faces in respect
to its nonrotating opposite
triangular face__wherewith the octahedron collapses into
one, flattened-out, two-vector-
length, equiedged triangle, which in turn consists of
four one-vector-edged, equiangled
triangles, each of which in turn consists of two congruent,
one-vector-long, equiedged
triangles. All eight triangles lie together as two congruent
sets of four small, one-vector-
long, equiedged triangles. This centrally congruent
axial force in turn plunges the two
centrally congruent triangles through the inertia of
the three sets of two congruent, edge-
hinged triangles on the three sides of the congruent
pair of central triangles which fold the
big triangle's corners around the central triangle in
the manner of the three petals folding
into edge congruence with one another to produce a tetrahedrally
shaped flower bud.
Thus is produced one tetrahedron consisting of four
quadrivalently congruent tetrahedra,
with each of its six edges consisting of four congruent
vectors. The tetrahedron thus
formed, pulsatively reacts by turning itself inside-out
to produce, in turn, another
quadrivalent, four-tetrahedra congruence; which visible-to-visible,
quadrivalent tetrahedral
inside-outing/outside-inning is pulsatively regenerative.
(See Illus.
461.08.)
|
|
|
905.36
Herewith we witness both visible and heretofore invisible
phases of each of
the single tetrahedra thus pulsatively involved. The
univalent, apex-to-apex-bonded, four
tetrahedra and the three-point-to-three-point, trivalent,
base-bonded, four tetrahedra are
both now made visible, because what was visible to the
point-to-point four was invisible to
the three-point-to-three-point four, and vice versa.
|
|
|
905.37
In the two extreme limit cases of jitterbug contraction__both
the positive-
negative and the negative-positive phases__the two cases
become alternately visible,
which results in the invisible phase of either case
becoming congruent with the other's
invisible phase: ergo rendering both states visible.
|
|
|
905.38
This pulsating congruence of both the alternately
quadrivalent visible phases
of the limit case contractions of the vector equilibrium
results in an octavalent tetrahedron;
i.e., with all the tetrahedron's eight pulsative intertransformabilities
simultaneously
realized and congruently oriented.
|
|
|
905.39
This hierarchy of events represents a 28-fold volumetric
contraction from the
extreme limit of univalently coherent expandability
of the ever-integrally-unit system of the
eight potential pulsative phases of self-intertransformability
of the tetrahedron as the
minimum structural system of all Universe. In summary
we have:
|
|
|
905.40
As we jitterbuggingly transform contractively and
symmetrically from the
20-volume bivalent vector equilibrium phase to the 8-volume
quadrivalent octahedral
phase, we pass through the icosahedral phase, which
is nonselfstabilizing and may be
stabilized only by the insertion of six additional external
vector connectors between the 12
external vertexes of the vector equilibrium travelling
toward convergence as the six
vertexes of the trivalent 4-volume octahedron. These
six vectors represent the edge-
vectors of one tetrahedron.
|
|
|
905.41
The 28-volume, univalent, nucleus-embracing, tetrahedral
array extends its
outer vertexes beyond the bounds of the nucleus-embracing,
closest-packed,
omnisymmetrical domain of the 24-volume cube formed
by superimposing eight Eighth-
Octahedra, asymmetrical, equiangle-based, three-convergent-90-degree-angle-apexed
tetrahedra upon the eight outward equiangular triangle
facets of the vector equilibrium.
We find that the 28-ness of free-space expandability
of the univalent, octahedral, nucleus
embracement must lose a volume of 4 (i.e., four tetrahedra)
when subjected to
omniclosest-packing conditions. This means that the
dynamic potential of
omniinterconnected tetrahedral pulsation system's volumetric
embracement capability of
28, upon being subjected to closest-packed domain conditions,
will release an elsewhere-
structurally-investable volume of 4. Ergo, under closest-packed
conditions, each nuclear
array of tetrahedra (each of which is identifiable energetically
with one energy quantum)
may lend out four quanta of energy for whatever tasks
may employ them.
|
|
|
905.42
The dynamic vs. kinetic difference is the same difference
as that of the
generalized, sizeless, metaphysically abstract, eternal,
constant sixness-of-edge, foumess-
of-vertex, and fourness-of-void of the only-by-mind-conceptual
tetrahedron vs. the only-
in-time-sized, special-case, brain-sensed tetrahedron.
This generalized quality of being
dynamic, as being one of a plurality of inherent systemic
conditions and potentials, parts of
a whole set of eternally co-occurring, complex interaccommodations
in pure, weightless,
mathematical principle spontaneously producing the minimum
structural systems, is indeed
the prime governing epistemology of wave quantum physics.
|
|
|
905.43
In consideration of the tetrahedron's quantum intertransformabilities,
we
have thus far observed only the expandable-contractable,
variable-bonding-permitted
consequences. We will now consider other dynamical potentials,
such as, for instance, the
axial rotatabilities of the respective tetras, octas,
and icosas.
|
|
|
905.44
By internally interconnecting its six vertexes with
three polar axes: X, Y, and
Z, and rotating the octahedron successively upon those
three axes, three planes are
internally generated that symmetrically subdivide the
octahedron into eight uniformly
equal, equiangle-triangle-based, asymmetrical tetrahedra,
with three convergent, 90-
degree-angle-surrounded apexes, each of whose volume
is one-eighth of the volume of
one octahedron: this is called the Eighth-Octahedron.
(See also Sec.
912.) The
octahedron, having a volume of four tetrahedra, allows
each Eighth-Octahedron to have a
volume of one-half of one tetrahedron. If we apply the
equiangled-triangular base of one
each of these eight Eighth-Octahedra to each of the
vector equilibrium's eight equiangle-
triangle facets, with the Eighth-Octahedra's three-90-degree-angle-surrounded
vertexes
pointing outwardly, they will exactly and symmetrically
produce the 24-volume, nucleus-
embracing cube symmetrically surrounding the 20-volume
vector equilibrium; thus with 8 × 1/2 = 4 being
added to the 20-volume vector equilibrium
producing a 24-volume total.
|
|
|
905.45
A non-nucleus-embracing 3-volume cube may be produced
by applying four
of the Eighth-Octahedra to the four equiangled triangular
facets of the tetrahedron. (See
Illus.
950.30.)
Thus we find the tetrahedral evolvement
of the prime number three as
identified with the cube. Ergo all the prime numbers__1,
2, 3, 5, 7__of the octave wave
enumeration system, with its zero-nineness, are now
clearly demonstrated as evolutionarily
consequent upon tetrahedral intertransformabilities.
|
|
|
905.46
Since the tetrahedron becomes systematically subdivided
into 24 uniformly
dimensioned A Quanta Modules (one half of which are
positive and the other half of which
are negatively inside-out of the other); and since both
the positive and negative A Quanta
Modules may be folded from one whole triangle; and since,
as will be shown in Sec.
905.62
the flattened-out triangle of the A Quanta Module
corresponds with each of the
120 disequilibrious LCD triangles, it is evidenced that
five tetrahedra of 24 A Quanta
Modules each, may have their sum-total of 120 A Modules
all unfolded, and that they may
be edge-bonded to produce an icosahedral spherical array;
and that 2 1/2 tetrahedra's 60 A
Quanta Modules could be unfolded and univalently (single-bondedly)
arrayed to produce
the same spheric icosahedral polyhedron with 60 visible
triangles and 60 invisible
triangular voids of identical dimension.
|
|
|
905.47
Conversely, 60 positive and 60 negative A Quanta Modules
could be folded
from the 120 A Module triangles and, with their "sharpest"
point pointed inward, could be
admitted radially into the 60-positive-60-negative tetrahedral
voids of the icosahedron.
Thus we discover that the icosahedron, consisting of
120 A Quanta Modules (each of
which is 1/24th of a tetrahedron) has a volume of 120/24
= 5 The icosahedron volume is 5
when the tetrahedron is 1; the octahedron 22 ; the cube
3; and the star-pointed, univalent,
eight-tetrahedra nuclear embracement is 28, which is
4 × 7; 28 also being the maximum
number of interrelationships of eight entities:
|
|
|
905.48
The three surrounding angles of the interior sharpest
point of the A Quanta
Module tetrahedron are each a fraction less than the
three corresponding central angles of
the icosahedron: being approximately one-half of a degree
in the first case; one whole
degree in the second case; and one and three-quarters
of a degree in the third case. This
loose-fit, volumetric-debit differential of the A Quanta
Module volume is offset by its
being slightly longer in radius than that of the icosahedron,
the A Module's radial depth
being that of the vector equilibrium's, which is greater
than that of the icosahedron, as
caused by the reduction in the radius of the 12 balls
closest-packed around one nuclear
ball of the vector equilibrium (which is eliminated
from within the same closest-radially-
packed 12 balls to reduce them to closest surface-packing,
as well as by eliminating the
nuclear ball and thereby mildly reducing the system
radius). The plus volume of the
fractionally protruded portion of the A Quanta Module
beyond the icosahedron's surface
may exactly equal the interior minus volume difference.
The balancing out of the small
plus and minus volumes is suggested as a possibility
in view of the exact congruence of 15
of the 120 spherical icosahedra triangles with each
of the spherical octahedron's eight
spherical equiangle faces, as well as by the exact congruence
of the octahedron and the
vector equilibrium themselves. As the icosahedron's
radius shortens, the central angles
become enlarged.
|
|
|
905.49
This completes the polyhedral progression of the omni-phase-bond-
integrated hierarchies of__1-2-3-4, 8__symmetrically expanded
and symmetrically
subdivided tetrahedra; from the 1/24th-tetrahedron (12
positive and 12 negative A Quanta
Modules); through its octavalent 8-in-1 superficial
volume-1; expanded progressively
through the quadrivalent tetrahedron; to the quadrivalent
octahedron; to the bivalent
vector equilibrium; to the univalent, 28-volume, radiant,
symmetrical, nucleus-embracing
stage; and thence exploded through the volumeless, flatout-outfolded,
double-bonded
(edge-bonded), 120-A-Quanta-Module-triangular array
remotely and symmetrically
surrounding the nuclear volumetric group; to final dichotomizing
into two such flatout half
(positive triangular) film and half (negative triangular)
void arrays, single-bonded (corner-
bonded), icosahedrally shaped, symmetrically nuclear-surrounding
systems.
|
|
|
905.50
Rotatability and Split Personality of Tetrahedron
|
|
|
905.51
Having completed the expansive-contractive, could-be,
quantum jumps, we
will now consider the rotatability of the tetrahedron's
six-edge axes generation of both the
two spherical tetrahedra and the spherical cube whose
"split personality's" four-triangle-
defining edges also perpendicularly bisect all of both
of the spherical tetrahedron's four
equiangled, equiedged triangles in a three-way grid,
which converts each of the four
equiangled triangles into six right-angle spherical
triangles__for a total of 24, which are
split again by the spherical octahedron's three great
circles to produce 48 spherical
triangles, which constitute the 48 equilibrious LCD
Basic Triangles of omniequilibrious
eventless eternity (see Sec.
453).
|
|
|
905.52
The spherical octahedron's eight faces become skew-subdivided
by the
icosahedron's 15 great circles' self-splitting of its
20 equiangular faces into six-each, right
spherical triangles, for an LCD spherical triangle total
of 120, of which 15 such right
triangles occupy each of the spherical octahedron's
eight equiangular faces__for a total of
120__which are the same 120 as the icosahedron's 15 great
circles.
|
|
|
905.53
The disequilibrious 120 LCD triangle = the equilibrious
48 LCD triangle ×
2½. This 2½ + 2½ = 5; which represents the icosahedron's
basic fiveness as split-
generated into 2½ by their perpendicular, mid-edge-bisecting
15 great circles. Recalling
the six edge vectors of the tetrahedron as one quantum,
we note that 6 + 6 + 6/2 is 1 + 1 +
1/2 = 2½ ; and that 2½ × 6 = 15 great circles. (This half-positive
and half negative
dichotomization of systems is discussed further at Sec.
1053.30ff.)
|
|
|
905.54
We find that the split personality of the icosahedron's
15-great-circle
splittings of its own 20 triangles into 120, discloses
a basic asymmetry caused by the
incompleteness of the 2½, where it is to be seen in
the superimposition of the spherical
icosahedron upon the spherical vector equilibrium. In
this arrangement the fundamental
prime number fiveness of the icosahedron is always split
two ways: 2½ positive phase and
2½ negative phase. This half-fiving induces an alternate
combining of the half quantum on
one side or the other: going to first three on one side
and two on the other, and vice versa.
|
|
|
905.55
This half-one-side/half-on-the-other induces an oscillatory
alternating 120-
degree-arc, partial rotation of eight of the spherical
tetrahedron's 20 equiangled triangles
within the spherical octahedron's eight triangles: 8
× 2½ = 20. We also recall that the
vector equilibrium has 24 internal radii (doubled together
as 12 radii by the congruence of
the four-great-circle's hexagonal radii) and 24 separate
internal vector chords. These 24
external vector chords represent four quanta of six
vectors each. When the vector
equilibrium jitterbuggingly contracts toward the octahedral
edge-vector doubling stage, it
passes through the unstable icosahedral stage, which
is unstable because it requires six
more edge-vectors to hold fixed the short diagonal of
the six diamond-shaped openings
between the eight triangles. These six equilength vectors
necessary to stabilize the
icosahedron constitute one additional quantum which,
when provided, adds 1 to the 4 of
the vector equilibrium to equal 5, the basic quantum
number of the icosahedron.
|
|
|
905.60
The Disequilibrium 120 LCD Triangle
|
|
|
905.61
The icosahedral spherical great-circle system displays: 12 vertexes surrounded by 10 converging angles; 20 vertexes surrounded by 6 converging angles; 30 vertexes surrounded by 4 converging angles
|
|
|
905.62
According to the Principle of Angular Topology (see
Sec.
224
), the 360
converging angle sinuses must share a 720-degree reduction
from an absolute sphere to a
chorded sphere: 720°/360° = 2°. An average of 2 degrees
angular reduction for each
comer means a 6 degrees angular reduction for each triangle.
Therefore, as we see in each
of the icosahedron's disequilibrious 120 LCD triangles,
the well-known architects and
engineers' 30°-60°-90° triangle has been spherically
opened to 36°-60°-90° __a "spherical
excess," as the Geodetic Survey calls it, of 6 degrees.
All this spherical excess of 6 degrees
has been massaged by the irreducibility of the 90-degree
and 60-degree corners into the
littlest corner. Therefore, 3036
in each of the spherical
icosahedron's 120 surface
triangles.
|
|
|
905.63
In subsiding the 120 spherical triangles generated
by the 15 great circles of
the icosahedron from an omnispherical condition to a
neospheric 120-planar-faceted
polyhedron, we produce a condition where all the vertexes
are equidistant from the same
center and all of the edges are chords of the same spherical
triangle, each edge having
been shrunk from its previous arc length to the chord
lengths without changing the central
angles. In this condition the spherical excess of 6
degrees could be shared proportionately
by the 90°, 60°, 30° flat triangle relationship which
factors exactly to 3:2:1. Since 6° =
1/30 of 180° , the 30 quanta of six each in flatout triangles
or in the 120 LCD spherical
triangles' 186 degrees, means one additional quantum
crowded in, producing 31 quanta.
|
|
|
905.64
Alternatively, the spherical excess of 6 degrees (one
quantum) may be
apportioned totally to the biggest and littlest corners
of the triangle, leaving the 60-degree,
vector equilibrium, neutral corner undisturbed. As we
have discovered in the isotropic
vector matrix nature coordinates crystallographically
in 60 degrees and not in 90 degrees.
Sixty degrees is the vector equilibrium neutral angle
relative to which life-in-time
aberrates.
|
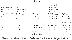 Table 905.65 |
905.65
By freezing the 60-degree center of the icosahedral
triangle, and by sharing
the 6-degree, spherical-planar, excess reduction between
the 36-degree and 90-degree
corners, we will find that the A Quanta Modules are
exactly congruent with the 120
internal angles of the icosahedron. The minus 5° 16'
closely approximates the one
quantum 6 + of spherical excess apparent at the surface,
with a comparable nuclear
deficiency of 5° 16'. (See Table 905.65.)
|
|
|
905.66
The Earth crust-fault angles, steel plate fractionation
angles, and ship's bow
waves all are roughly the same, reading approximately
70-degree and 110-degree
complementation.
|
|
|
|
|
|
|
|
|
|
| Next Section: 905.70 |