|
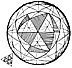
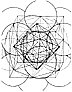
982.71
 The significance of this unified field as defining
and embracing the minimum-
maximum limits of the inherent nuclear domain limits
is demonstrated by the nucleus-
concentric, symmetrical, geometrical hierarchy wherein
the rhombic dodecahedron
represents the smallest, omnisymmetrical, selfpacking,
allspace-filling, six-tetra-volume,
uniquely exclusive, cosmic domain of each and every
closest-packed, unit-radius sphere.
Any of the closest-packed, unit-radius spheres, when
surrounded in closest packing by 12
other such spheres, becomes the nuclear sphere, to become
uniquely embraced by four
successive layers of surrounding, closest-packed, unit-radius
spheres__each of which four
layers is uniquely related to that nucleus__with each
additional layer beyond four
becoming duplicatingly repetitive of the pattern of
unique surroundment of the originally
unique, first four, concentric-layered, nuclear set.
It is impressive that the unique nuclear
domain of the rhombic dodecahedron with a volume of
six contains within itself and in
nuclear concentric array:
The significance of this unified field as defining
and embracing the minimum-
maximum limits of the inherent nuclear domain limits
is demonstrated by the nucleus-
concentric, symmetrical, geometrical hierarchy wherein
the rhombic dodecahedron
represents the smallest, omnisymmetrical, selfpacking,
allspace-filling, six-tetra-volume,
uniquely exclusive, cosmic domain of each and every
closest-packed, unit-radius sphere.
Any of the closest-packed, unit-radius spheres, when
surrounded in closest packing by 12
other such spheres, becomes the nuclear sphere, to become
uniquely embraced by four
successive layers of surrounding, closest-packed, unit-radius
spheres__each of which four
layers is uniquely related to that nucleus__with each
additional layer beyond four
becoming duplicatingly repetitive of the pattern of
unique surroundment of the originally
unique, first four, concentric-layered, nuclear set.
It is impressive that the unique nuclear
domain of the rhombic dodecahedron with a volume of
six contains within itself and in
nuclear concentric array:
| __ | the unity-one-radiused sphere of volume five; |
| __ | the octahedron of volume four; |
| __ | the cube of volume three; |
| __ | the prime vector equilibrium of volume 2 l/2; and |
| __ | the two regular (positive and negative) tetrahedra
of volume one each. |
This succession of 1, 2, 3, 4, 5, 6 rational volume
relationships embraces the first four
prime numbers 1, 2, 3, and 5. (See Illus.
982.61 in
color section.) The volume-24 (tetra)
cube is the largest omnisymmetrical self-packing, allspace-filling
polyhedron that exactly
identifies the unique domain of the original 12-around-one,
nuclear-initiating, closest
packing of unit-radius spheres. The unit quantum leap
of 1__going to 2__going to
3__going to 4__going to 5__going to 6, with no step greater
than 1, suggests a unique
relationship of this set of six with the sixness of
degrees of freedom.8
(Footnote 8: For further suggestions of the relationship between the rhombic
dodecahedron and the degrees of freedom see Sec.
426
537.10
954.47.)
|

 Starting With Parts: The Nonradial Line: Since humanity
started with
parallel lines, planes, and cubes, it also adopted the
edge line of the square and cube as the
prime unit of mensuration. This inaugurated geomathematical
exploration and analysis
with a part of the whole, in contradistinction to synergetics'
inauguration of exploration
and analysis with total Universe, within which it discovers
whole conceptual systems,
within which it identifies subentities always dealing
with experimentally discovered and
experimentally verifiable information. Though life started
with whole Universe, humans
happened to pick one part__the line, which was so short
a section of Earth arc (and the
Earth's diameter so relatively great) that they assumed
the Earth-scratched-surface line to
be straight. The particular line of geometrical reference
humans picked happened not to be
the line of most economical interattractive integrity.
It was neither the radial line of
radiation nor the radial line of gravity of spherical
Earth. From this nonradial line of
nature's event field, humans developed their formulas
for calculating areas and volumes of
the circle and the sphere only in relation to the cube-edge
lines, developing empirically the
"transcendentally irrational," ergo incommensurable,
number pi (
Starting With Parts: The Nonradial Line: Since humanity
started with
parallel lines, planes, and cubes, it also adopted the
edge line of the square and cube as the
prime unit of mensuration. This inaugurated geomathematical
exploration and analysis
with a part of the whole, in contradistinction to synergetics'
inauguration of exploration
and analysis with total Universe, within which it discovers
whole conceptual systems,
within which it identifies subentities always dealing
with experimentally discovered and
experimentally verifiable information. Though life started
with whole Universe, humans
happened to pick one part__the line, which was so short
a section of Earth arc (and the
Earth's diameter so relatively great) that they assumed
the Earth-scratched-surface line to
be straight. The particular line of geometrical reference
humans picked happened not to be
the line of most economical interattractive integrity.
It was neither the radial line of
radiation nor the radial line of gravity of spherical
Earth. From this nonradial line of
nature's event field, humans developed their formulas
for calculating areas and volumes of
the circle and the sphere only in relation to the cube-edge
lines, developing empirically the
"transcendentally irrational," ergo incommensurable,
number pi (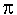 ), 3.14159 . . . ad
infinitum, which provided practically tolerable approximations
of the dimensions of circles
and spheres.
), 3.14159 . . . ad
infinitum, which provided practically tolerable approximations
of the dimensions of circles
and spheres.