Cosmic Commensurability of Time and Size Magnitudes:
Each degree
of 360 degrees of circular arc is subdivided into 60
minutes and the minutes into 60
seconds each. There are 1,296,000 seconds of arc in
a circle of 360 degrees.
|
|
1238.31
One minute of our 8,000-mile-diameter planet Earth's
great circle arc = one
nautical mile = 6,076 feet approximately. A one-second
arc of a great circle of Earth is
6,076/60 = 101.26 feet, which means one second of great-circle
arc around Earth is
approximately 100 feet, or the length of one tennis
court, or one-third of the distance
between the opposing teams' goal posts on a football
field. We can say that each second of
Earth's great circle of arc equals approximately 1,200
inches (or 1,215.12 "exact"). There
are 2 1/2 trillion atomic-nucleus diameters in one inch.
A hundredth of an inch is the
smallest interval clearly discernible by the human eye.
There are 25 billion atomic-nucleus
diameters in the smallest humanly visible "distance"
or linear size increment. A hundredth
of an inch equals 1/120,000th of a second of great-circle
arc of our spherical planet Earth.
This is expressed decimally as .0000083 of a second
of great-circle arc = .01 inch; or it is
expressed scientifically as .01 inch = 83 × 10-7. A
hundredth of an inch equals the
smallest humanly visible dust speck; therefore: minimum
dust speck = 83 × 10-7 seconds
of arc, which equals 25 billion atomic-nucleus diameters__or
2 1/2 million angstroms. This
is to say that it requires seven places to the right
of the decimal to express the fractional
second of the greatcircle arc of Earth that is minimally
discernible by the human eye.
|
|
|
1238.40
Fourteen-illion Scheherazade Number: The Fourteen-illion
Scheherazade
Number includes the first 15 primes, which are:
1n·212·38·56·76·116·136·172·19·23·29·31·37·41·43 It reads: 3,128,581,583,194,999,609,732,086,426,156,130,368,000,000 |
|
|
1238.41
Declining Powers of Factorial Primes: The recurrence
of the prime
number 2 is very frequent. The number of operational
occasions in which we need the
prime number 43 is very less frequent than the occasions
in which the prime numbers 2, 3,
5, 7, and 11 occur. This Scheherazade Number provides
an abundance of repowerings of
the lesser prime numbers characterizing the topological
and vectorial aspects of
synergetics' hierarchy of prime systems and their seven
prime unique symmetrical aspects
(see Sec.
1040)
adequate to take care of all the topological
and trigonometric
computations and permutations governing all the associations
and disassociations of the
atoms.
|
|
|
1238.42
We find that we can get along without multirepowerings
after the second
repowering of the prime number 17. The prime number
17 is all that is needed to
accommodate both the positive and negative octave systems
and their additional zero-
nineness. You have to have the zero-nine to accommodate
the noninterfered passage
between octave waves by waves of the same frequency.
(See Secs.
1012
and
1223.)
|
|
|
1238.43
The prime number 17 accommodates all the positive-negative,
quanta-wave
primes up to and including the number 18, which in turn
accommodates the two nines of
the invisible twoness of all systems. It is to be noted
that the harmonics of the periodic
table of the elements add up to 92:
There are five sets of 18, though the 36 is not always so recognized. Conventional analysis of the periodic table omits from its quanta accounting the always occurring invisible additive twoness of the poles of axial rotation of all systems. (See Sec. 223.11 and Table 223.64, Col. 7.) |
|
|
1238.50
Properties: The 3 fourteen-illion magnitude Scheherazade
Number has 3 × 1043
whole-number places, which is 1037 more integer places
than has the 1 × 106 number
expressing the 1,296,000 seconds in 360 degrees of whole-circle
arc, and can therefore
accommodate rationally not only calculations to approximately
1/l00th of an inch (which is
the finest increment resolvable by the human eye), but
also the 10-7 power of that
minimally visible magnitude, for this 3×1043 SSRCD
has enough decimal places to express
rationally the 22-billion-light-years-diameter of the
omnidirectional, celestial-sphere limits
thus far observed by planet Earth's humans expressed
in linear units measuring only
l,000ths of the diameter of one atomic nucleus.
|
|
|
1238.51
Scheherazade Numbers: 47: The first prime number beyond
the
trigonometric limit is 47. The number 47 may be a flying
increment to fill allspace, to fill
out the eight triangular facets of the non-allspace-filling
vector equilibrium to form the
allspace-filling first nuclear cube. If 47 as a factor
produces a Scheherazade Number with
mirrors, it may account not only for all the specks
of dust in the Universe but for all the
changes of cosmic restlessness, accounting the convergent-divergent
next event, which
unbalances the even and rational whole numbers. If 47
as a factor does not produce a
Scheherazade Number with mirrors, it may explain that
there can be no recurring limit
symmetries. It may be that 47 is the cosmic random element,
the agent of infinite change.
|
|
|
1238.52
Addendum Inspired by inferences of Secs.
1223.12,
1224.30-34
inclusive and
1238.51,
just before going to press with Synergetics
2, we obtained the following 71
integer, multi-intermirrored, computer-calculated and
proven, volumetric (third power)
Scheherazade number which we have arranged in ten, "sublimely
rememberable," unique
characteristic rows.
212·38·56·76·
116·136·174·193·
233·293·313·373·
413·433·473
the product of which is
616,494,535,0,868
49,2,48,0 51,88 27,49,49 00,6996,185 494,27,898 35,17,0 25,22, 73,66,0 864,000,000 If all the trigonometric functions are reworked using this 71 integer number, embracing all prime numbers to 50, to the third power, employed as volumetric, cyclic unity, all functions will prove to be whole rational numbers as with the whole atomic populations. |
|
|
1238.60
Size Magnitudes
An Atomic Nucleus Diameter = A.N.D. =
|
|
|
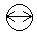
1238.70
|
|
|
1238.80
Number Table: Significant Numbers (see Table
1238.80)
|
|
|
1239.00
Limit Number of Maximum Asymmetry
|
|
|
1239.10
Powers of Primes as Limit Numbers: Every so often out
of an apparently
almost continuous absolute chaos of integer patterning
in millions and billions and
quadrillions of number places, there suddenly appears
an SSRCD rememberable number in
lucidly beautiful symmetry. The exponential powers of
the primes reveal the beautiful
balance at work in nature, which does not secrete these
symmetrical numbers in irrelevant
capriciousness. Nature endows them with functional significance
in her symmetrically
referenced, mildly asymmetrical, structural formulations.
The SSRCD numbers suddenly
appear as unmistakably as the full Moon in the sky.
|
|
|
1239.11
There is probably a number limit in nature that is
adequate for the rational,
whole-number accounting of all the possible general
atomic systems' permutations. For
instance, in the Periodic Table of the Elements, we
find 2, 8, 8, 18. These number sets
seem familiar: the 8 and the 18, which is twice 9, and
the twoness is perfectly evident. The
largest prime number in 18 is 17. It could be that if
we used all the primes that occur
between 1 and 17, multiplied by themselves five times,
we might have all the possible
number accommodations necessary for all the atomic permutations.
|
|
|
1239.20
Pairing of Prime Numbers: I am fascinated by the fundamental
interbehavior of numbers, especially by the behavior
of primes. A prime cannot be
produced by the interaction of any other numbers. A
prime, by definition, is only divisible
by itself and by one. As the integers progress, the
primes begin to occur again, and they
occur in pairs. That is, when a prime number appears
in a progression, another prime will
appear again quite near to it. We can go for thousands
and thousands of numbers and then
find two primes appearing again fairly close together.
There is apparently some kind of
companionship among the primes. Euler, among others,
has theories about the primes, but
no one has satisfactorily accounted for their behavior.
|
|
|
1239.30
Maximum Asymmetry: In contrast to all the nonmeaning,
the
Scheherazade Numbers seem to emerge at remote positions
in numerical progressions of
the various orders. They emerge as meaning out of nonmeaning.
They show that nature
does not sustain disorder indefinitely.
|
|
|
1239.31
From time to time, nature pulses inside-outingly through
an omnisymmetric
zerophase, which is always our friend vector equilibrium,
in which condition of sublime
symmetrical exactitude nature refuses to be caught by
temporal humans; she refuses to
pause or be caught in structural stability. She goes
into progressive asymmetries. All
crystals are built in almost-but-not quite-symmetrical
asymmetries, in positive or negative
triangulation stabilities, which is the maximum asymmetry
stage. Nature pulsates
torquingly into maximum degree of asymmetry and then
returns to and through symmetry
to a balancing degree of opposite asymmetry and turns
and repeats and repeats. The
maximum asymmetry probably is our minus or plus four,
and may be the fourth degree,
the fourth power of asymmetry. The octave, again.
|
| Afterpiece |