1010.00 Prime Volumes

1010.01 A prime volume has unique domains but does not have a nucleus.
1010.02 A prime volume is different from a generalized regenerative system. Generalized regenerative systems have nuclei; generalized prime volumes do not.
1010.03 There are only three prime volumes: tetrahedron, octahedron, and icosahedron. Prime volumes are characterized exclusively by external structural stability.
1010.10 Domain and Quantum: The unique insideness domain of a prime system is, in turn, a prime volumetric domain, which is always conceptually defined by the system's topological vertex-interconnecting lines and the areas finitely enclosed by those lines. (V + F = L + 2.) Prime volumetric domain provides space definition independent of size.
1010.11 Prime volumetric domain and prime areal domain together provide space conceptuality independent of size, just as the tetrahedron provides prime structural system conceptuality independent of size.
1010.12 Complex bubble aggregates are partitioned into prime volumetric domains by interiorly subdividing prime areal domains as flat drawn membranes.
1010.13 A prime volumetric domain has no volumetric nucleus. A prime areal domain has no planar nucleus. So we have prime system volumetric domains and prime system areal domains and linear interconnections of all vertexes__all with complete topological conceptual interpatterning integrity utterly independent of size.
1010.14 This frees conceptual-integrity comprehending and all the prime constituents of prime-pattern integrity, such as "volume," "area," and "line," from any special-case quantation. All the prime conceptuality of omnitopology is manifest as being a priori and eternally generalized phenomena. Thus quantum as prime-structural-system volume is eternally generalized, ergo, transcends any particulate, special-case, physical-energy quantation. Generalized quanta are finitely independent because their prime volumetric- domain-defining lines do not intertouch.
1010.20 Nonnuclear Prime Structural Systems: The domain of the tetrahedron is the tetrahedron as defined by four spheres in a tetrahedral, omniembracing, closest-packed tangency network. The domain of an octahedron is vertexially defined by six spheres closest packed in omnitriangular symmetry. The domain of an icosahedron is vertexially defined by 12 spheres omnicircumferentially intertriangulated and only circumferentially symmetrically triangulated in closest packing without a nucleus (in contradistinction to the center sphere of the vector equilibrium, whose 12 outer sphere centers define the vector equilibrium's 12 vertexes; all 13 of the vector equilibrium's spheres are intersymmetrically closest packed both radially and circumferentially).
1010.21 All of the three foregoing non-nuclear-containing domains of the tetrahedron, octahedron, and icosahedron are defined by the four spheres, six spheres, and twelve spheres, respectively, which we have defined elsewhere (see Sec. 610.20, "Omnitriangular Symmetry: Three Prime Structural Systems") as omnitriangulated systems or as prime structural systems and as prime volumetric domains. There are no other symmetrical, non-nuclear-containing domains of closest-packed, volume-embracing, unit-radius sphere agglomerations.
1010.22 While other total closest-packed-sphere embracements, or agglomerations, may be symmetrical or superficially asymmetrical in the form of crocodiles, alligators, pears, or billiard balls, they constitute complexedly bonded associations of prime structural systems. Only the tetrahedral, octahedral, and icosahedral domains are basic structural systems without nuclei. All the Platonic polyhedra and many other more complex, multidimensional symmetries of sphere groupings can occur. None other than the three- and-only prime structural systems, the tetrahedron, octahedron, and icosahedron, can be symmetrically produced by closest-packed spheres without any interioral, i.e., nuclear, sphere. (See Secs. 532.40, 610.20, 1010.20 and 1011.30.)
1011.00 Omnitopology of Prime Volumes
1011.10 Prime Enclosure: Omnitopology describes prime volumes. Prime volume domains are described by Euler's minimum set of visually unique topological aspects of polyhedral systems. Systems divide Universe into all Universe occurring outside the system, all Universe occurring inside the system, and the remainder of Universe constituting the system itself. Any point or locus inherently lacks insideness. Two event points cannot provide enclosure. Two points have betweenness but not insideness. Three points cannot enclose. Three points describe a volumeless plane. Three points have betweenness but no insideness. A three-point array plus a fourth point that is not in the plane described by the first three points constitutes prime enclosure. It requires a minimum of four points to definitively differentiate cosmic insideness and outsideness, i.e., to differentiate macrocosm from microcosm, and to differentiate both of them from here and now.
1011.11 Systems are domains of volumes. One difference between a domain and a volume is that a domain cannot have an interior point, because if it did, it would be subject to more economical subdivision. For instance, the vector equilibrium is a system and has a volume, but it consists of 20 domains. A vector equilibrium is not a prime domain or a prime volume, because it has a nucleus and consists of a plurality of definitive volumetric domains. The vector equilibrium is inherently subdivisible as defined by most economical triangulation of all its 12 vertexes into eight tetrahedra and 12 quarter-octahedra, constituting 20 identically volumed, minimum prime domains.
1011.20 Hierarchy of Nuclear Aggregations: The prime nuclear aggregation of spheres around one sphere is the vector equilibrium. Vector equilibrium constitutes the prime nuclear group because it consists of the least number of spheres that can be closest packed omnitangentially around one nuclear sphere. The vector equilibrium provides the most volumetrically economical pattern of aggregation of 12 balls around a nuclear ball of the same diameter as the 12 surrounding balls; the 13th ball is the center. In other words, is the lowest possible number connected with a structurally stable triangulated nucleus, being omnitriangularly interconnected both radially and circumferentially.
1011.21 An octahedron is at minimum a prime system. Prime systems are generalized. To be realized experimentally in special-case time-space, the octahedron must consist of a high-frequency aggregate of octahedral and tetrahedral components. An octahedral system gains a nucleus with 19 balls, i.e., with 18 uniradius balls around one, as against the minimum nucleated (four-frequency) tetrahedral array of 35 balls, i.e., with 34 balls symmetrically around one. So the octahedron gains a nucleus at a lower frequency than does the tetrahedron.
1011.22 Whether at zero-frequency or multifrequency state, the icosahedron cannot have a tangentially contiguous, ergo statically structural, nuclear sphere of the same radius as those of its closest-packed, single, outer-layer array. It can only have a dynamically structured nucleus whose mass is great enough to impose critical-proximity central dominance over its orbitally icosahedrally arrayed, remotely co-orbiting constellation of concentrated energy events.
1011.23 The vector equilibrium has four hexagonally perimetered planes intersecting each other symmetrically at its center; while the octahedron has only three square- perimetered planes symmetrically intersecting one another at its center. The hexagon has room at its center for a uniradius circle tangent to each of the six circles tangent to one another around it; whereas the square does not have room for such a uniradius circle. Wherefore the minimal four-dimensional coordinate system of the vector equilibrium is the minimum inherently nucleated system. (This is why mathematical physics employing three- dimensional, XYZ coordination can only accommodate its experimental evidence of the atomic nucleus by amorphous mathematics.) Like the octahedron, the vector equilibrium also has eight triangular facets; while also explosively extroverting the octahedron's three square central planes, in two ways, to each of its six square external facets, thus providing seven unique planes, i.e. seven-dimensionality. And while the octahedron develops a nucleus at a lower number than does the tetrahedron__or more economically than a tetrahedron__it is indicated that the nuclear arrays are symmetrical and play very great parts in compound chemistry. (The cube develops a nucleus only at a relatively high frequency.) In each one of these, there may be hierarchies that identify the difference between organic and inorganic chemistries. Due to the fact that there are nuclear aggregations in symmetry to which all of our chemistries relate, we may find an organic and inorganic identification of the tetrahedral and octahedral nucleations. The nonnuclear, exclusively volumetric, single-layer, closest-packed, icosahedral aggregate may be identified with the electron "shells" of the compounding atoms.
1011.30 Prime Tetra, Octa, and Icosa: Prime means the first possible realization. It does not have frequency. It is subfrequency. One or zero are subfrequency. Interval and differentiation are introduced with two. Frequency begins with three__with triangle, which is the minimum cyclic closed circuitry.
1011.31 Three linear events have two intervals, which is the minimum set to invoke the definition frequency. But it is an "open" circuit. The circuit is closed and operative when the triangle is closed and the same three events produce three equi-intervals, rather than two. Equi-interval = "tuned." This is why wave-frequency relationships have a minimum limit and not an infinite series behavior.
1011.32 Frequency and size are the same phenomena. Subfrequency prime tetra, prime octa, and prime icosa are each constituted of only one edge module per triangular facet. While generalizably conceptual, the prime structural systems and their prime domains__linear, areal, and volumetric__are inherently subfrequency, ergo, independent of time and size.
1011.33 Special case always has frequency and size-time.
1011.34 Generalization is independent of size and time, but the generalization principle must be present in every special case of whatever magnitude of size or time.
1011.35 Prime tetrahedra and octahedra do not have nuclei. In contradistinction to prime tetrahedra and prime octahedra, some complex tetrahedra, complex octahedra, and complex cubes do have a nucleus. They do not develop structurally in strict conformity to closest packing to contain an internal or nuclear ball until additional closest-packed, uniradius sphere layers are added. For instance, the cubical array produced by nesting eight uniradius spheres in the center of the eight triangulated sphere arrays of the nuclear- balled vector equilibrium produces eight tetrahedra single-bondedly arrayed around a nuclear ball. Additional, and symmetrically partial, layers require identification as frequency of reoccurrence of concentric shell embracement. In contradistinction to the other two prime system domains, however, the icosahedron does not accommodate additional closest-packed sphere layers and never develops a static structural nucleus. The icosahedron's closest-packing capability is that of circumferential propagation of only one omni-intertriangulated uniradius sphere and can increase its frequency only as one shell and not as a nucleus.
1011.36 If the icosahedron does develop a further outward shell, it will have to discard its internal shell because the central angles of the icosahedron will not allow room for unit-radius spheres of two or more closest-packed omnitriangulated concentric shells to be constructed. Only one closest-packed shell at a time is permitted. Considered internally, the icosahedron cannot accommodate e- en one uniradius, tangentially contiguous, interior or nuclear sphere of equal radius to those of its closest-packed, uniradius, outer shell.
1011.37 Speaking externally, either "prime" or complex "frequency" tetrahedra and octahedra may interagglomerate with one another close-packingly to fill allspace, while icosahedron may never do so. The icosahedra may be face-associated to constitute an ultimately large octahedral structure. Icosahedra may also symmetrically build independent, closest-packed, tetrahedral arrays outwardly on each of their multi- frequenced, 20 triangular facets. Thus it is seen that the icosahedral closest packing can only grow inside-outedly, as does the vector equilibrium grow internally, i.e. inside- inwardly.
1011.38 While the regular icosahedron's radius is shorter in length than its external edge chords, the vector equilibrium has the same radius as each of its edge chords; which explains the vector equilibrium's tolerance of a nucleus and the icosahedron's intolerance of a nucleus.
1011.40 Congruence of Vectors: All vector equilibria of any frequency reveal vectorially that their radially disassociative forces always exactly and balancingly contain their circumferentially integrated__and therefore more embracing than internally disintegrating__forces as manifest by their vectorial edge chords. The vector equilibrium consists of four symmetrically interacting hexagonal planes. Each hexagon displays six radially disintegrative, independently operative, therefore uncompounded, central vectors and their equal-magnitude six, always cooperatively organized and compounded, circumferential chord vectors. Sum-totally, the four hexagons have 24 radial disintegrative vectors and 24 chordally integrative vectors, with the chordals occurring as four closed sets of six vectors each and the radials as four open sets of six vectors each. The planes of any two hexagons of the set of four intersect one another in such a manner that the radii of any two intersecting planes are congruent, while the chords are not. This paired congruency of the 24 radial-disintegrative vectors of the four hexagons reduces their visible number to 12. The 24 chordally integrative vectors remain separate and visible as 24 finitely closed in four embracing sets of six each.
1011.41 The phenomenon "congruence of vectors" occurs many times in nature's coordinate structuring, destructuring, and other intertransformings, doubling again sometimes with four vectors congruent, and even doubling the latter once again to produce eight congruent vectors in limit-transformation cases, as when all eight tetrahedra of the vector equilibrium become congruent with one another. (See Sec. 461.08.) This phenomenon often misleads the uninformed observer.
1011.50 Instability of Vector Equilibrium: If we remove the 12 internal, congruently paired sets of 24 individual radii and leave only the 24 external chords, there will remain the eight corner-interlinked, externally embracing triangles, each of which (being a triangle) is a structure. Between the eight triangular external facets of the vector equilibrium, there also occur six squares, which are not structures. The six square untriangulated faces are the external facets of six nonstructurally stabilized half-octahedra, each of whose four central triangular faces had been previously defined by the now removed 24 radially paired vectors of the vector equilibrium. A half-octahedron, to be stable, has to be complementingly square-face-bonded with its other half. The prime vector equilibrium has only these six half-octahedra, wherefore the circumferential instability of its six square faces invites structural instability. Thus deprived of its internal triangular structuring by removal of all its radial vectors, the vector equilibrium becomes disequilibrious.
1011.51 The prime vector equilibrium has a nucleus surrounded, close-packingly and symmetrically, by 12 uniradius spheres. (See Illus. 222.01.) As we add unit radius sphere layers to the prime vector equilibrium, the 12 balls of the first, or prime, outer layer become symmetrically enclosed by a second closest-packed, unit radius layer of 42 balls circumferentially closest packed. This initiates a vector equilibrium with modular edge and radius intervals that introduce system frequency at its minimum of two.2

(Footnote 2: The number of balls in the outer shell of the vector equilibrium = 10 F2 + 2. The number 42, i.e., F2, i.e., 22 = 4, multiplied by 10 with the additive 2 = 42.)
1011.52 The edge frequency of two intervals between three balls of each of the vector equilibrium's 24 outer edges identifies the edges of the eight outer facet triangles of the vector equilibrium's eight edge-bonded (i.e., double-bonded) tetrahedra, whose common internal vertex is congruent with the vector equilibrium's nuclear sphere. In each of the vector equilibrium's square faces, you will see nine spheres in planar arrays, having one ball at the center of the eight (see Illus. 222.01), each of whose eight edge spheres belong equally to the adjacent tetrahedra's outwardly displayed triangular faces. This single ball at the center of each of the six square faces provides the sixth sphere to stabilize each of the original six half-octahedra formed by the nuclear ball of the vector equilibrium common with the six half-octahedra's common central vertex around the six four-ball square groups showing on the prime vector equilibrium's surface. This second layer of 42 spheres thus provides the sixth and outermost ball to complete the six-ball group of a prime octahedron, thus introducing structural stability increasing at a fourth-power rate to the vector equilibrium.
1011.53 With the 42-ball layer added to the vector equilibrium, there is no ball showing at the center of any of the triangular faces of the vector equilibrium. The three- ball edges of the 42-ball vector equilibrium provide a frequency of two. Three spheres in a row have two spaces between them. These interconnecting spaces between the centers of area of the adjacent spheres constitute the vectorial interconnections that provide the energetic, or force, frequency of the described systems.
1011.54 Then we come to the next concentric sphere layer, which has 92 balls; its frequency is three, but there are four balls to any one edge. The edges are all common to the next facet, so we only have to credit the balls to one facet or another at any one time; however, we have to do it in total overall accounting, i.e., in terms of how many balls are sum-totally involved in each of the concentrically embracing layers.
1011.55 With the four-ball edge F3, for the first time, a ball appears in the center of each of the eight triangular facets. These central balls are potential nuclei. They will not become new vector-equilibrium nuclei until each potential nuclear sphere is itself surrounded by a minimum of two completely encompassing layers. These potential new nuclei (potentially additional to the as yet only one nucleated sphere at the center of the prime vector equilibrium) occur in the planar triangular facets of the vector equilibrium's eight tetrahedra, which, being tetrahedra, are structural-system integrities (in contradistinction to its six half-octahedra, which__until fortified by their sixth outer-vertex balls of the two-frequency vector equilibrium__were structurally unstable).
1011.56 Though there is one ball in the center of each of the eight triangular facets of the F3 vector equilibrium, those balls are exposed on the outer surface of their respective tetrahedra and are not omnidirectionally and omnitangentially enclosed, as they would have to be to constitute a fully developed regenerative-system nucleus. Though outer- facetly centered (i.e., planarly central), those eight F3, triangularly centered balls are not nuclei. To become nuclei, they must await further symmetrically complete, concentric, closest-packed, vector-equilibrium shell embracements which bring about a condition wherein each of the eight new potential nuclei are embraced omnidirectionally and omnitangentially in closest-packed triangulation by a minimum of two shells exclusively unique to themselves, i.e., not shared by any neighboring nuclei. The F3 vector equilibrium's triangular facets' central surface-area balls are, however, the initial appearance in symmetrical, concentric, vector-equilibrium shell frequency growth of such potentially developing embryo nuclei. They are the first potential nuclei to appear in the progressive closest-packed, symmetrical, concentric layer enclosing of one prime regenerative system's primally nucleated vector equilibrium.
1011.57 But at F3 we still have only one true nuclear ball situated symmetrically at the volumetric center of three layers: the first of 12, the next of 42, and the outer layer of 92 balls. There is only one ball in the symmetrical center of the system. This three-layer aggregate has a total of 146 balls; as noted elsewhere (see Sec. 419.05) this relates to the number of neutrons in Uranium Element #92.
1011.58 Any sphere is in itself a potential nucleus, but it has to have 12 spheres close- packingly and omni-intertangentially embracing it to become a prime nucleated, potentially regenerative system. To stabilize its six half-octahedra requires a second layer of 42 balls. The potentially regenerative prime nucleus can have the first F0 layer of 12-around-one nucleus, and the next (F2) layer of 42 around both the nucleus and the first layer, without any new potential nucleus occurring in either of those first two concentric layers. So the vector equilibrium is a nuclear uniqueness for the first layer of 12 and the next layer of 42, with no other potential nucleus as yet appearing in its system__in its exterior shell's structural triangular facets__to challenge its nuclear pristinity.
1011.59 While there is a ball in the center of the square faces at the two-frequency, 42-ball level, those square cross sections of half-octahedra are not stable structures. Those square-centered balls are literally structurally superficial, ergo they are extra balls that show up but are not structurally stable in any way. They may be released to further re- form themselves into four-ball, prime, tetrahedral, structural systems, or they may be borrowed away from the nuclear system by another nuclear system__as does occur in chemical combines__without damaging the borrowed-from system's structural integrity. The four balls that occur in the core of the square facets of the F3, 92-ball shell are also borrowable extra balls.
1011.60 In the 92-ball, F3 third shell, eight potential nuclei occur in the triangular facets. "Four" and "square" do not constitute a structural array. To be structural is to be triangulated. Four balls also occur in each of the square facets, whereas one ball had occurred in the center of each of the six square facets of the previous F2, 42-ball layer. This means that at the F3, 92-ball layer, there are five balls in each of the six square-face centers. These five will be complemented by one or more, thus to form six new, detachable, nonnucleated, prime octahedra in the F4, 162-ball layer by a square group of nine balls in each of the six square facets of the vector equilibrium. The center ball of these nine will now join with the four balls of the F3 layer and the one ball of the F2 layer to form altogether a prime, closest-packed octahedron having no nucleus of its own.
1011.61 At the F4, 162-ball layer, the eight potential nuclei occurring in the mid- triangle faces of the F3 layer are now omnisurrounded, but as we have seen, this means that each has as yet only the 12 balls around it of the F0 nuclear-development phase. Not until the F5, 252-ball layer occurs do the eight potential second-generation nuclei become structurally enclosed by the 42-ball layer, which has as yet no new potential nuclei showing on its surface__ergo, even at the F5 level, the original prime nucleus considered and enclosingly developed have not become full-fledged, independently qualified, regenerative nuclei. Not until F6 and the 362-ball layer has been concentrically completed do we now have eight operatively new, regenerative, nuclear systems operating in partnership with the original nucleus. That is, the first generation of omnisymmetrical, concentric, vector equilibrium shells has a total of nine in full, active, operational condition. These nine, 8 + 1, may have prime identification with the eight operationally intereffective integers of arithmetic and the ninth integer's zero functioning in the prime behaviors of eternally self-regenerative Universe. We may also recall that the full family of Magic Numbers of the atomic isotopes modeled tetrahedrally occurs at the sixth frequency (see Sec. 995).
1011.62 The potential nucleated octahedra that were heralding their eventual development when the six prime (nonnucleated) octahedra occurred at the F4 level do not develop to full threefold, concentric, shell embracement as operational nuclei for several levels beyond that which had produced the second-generation eight vector-equilibrium nuclear integrities. We become also intrigued to speculate on the possible coincidence of the prime patternings developing here in respect to the 2, 8, 8, 18, 18, etc., sequences . . . of the Periodic Table of the Elements.
1012.00 Nucleus as Nine = None = Nothing
1012.01 Nucleus as nine; i.e., non (Latin); i.e., none (English); i.e., nein (German); i.e., neuf (French); i.e., nothing; i.e., interval integrity; i.e., the integrity of absolute generalized octaval cosmic discontinuity accommodating all special-case "space" of space- time reality. (See Secs. 415.43 and 445.10.)
1012.10 Positive-Negative Wave Pattern: Both the gravitational and the radiational effects operate exclusively in respect to and through the nucleus, whose unique domains multiply in eighths. Completion of the absolute initial uniqueness of pattern evolution of the nucleus itself brings in the nine as nothingness. How does this happen?
1012.11 Let us take three balls arranged in a triangle. We then take two other uniradius tangent balls lying in the same plane and address them symmetrically to any one corner-ball of the first three so that we have two rows of three balls crossing one another with one ball centrally common to both three-ball lines; so that we have two symmetrically arrayed triangles with one common corner. Obviously the center ball__like a railway switch__has to serve alternately either one three-ball track or the other, but never both at the same time, which would cause a smash-up. If we do the same thing four-dimensionally for the eight tetrahedra of the vector equilibrium, we find that the nuclear center ball is accommodating any one or any pair of the eight tetrahedra and is interconnecting them all. Externally, the eight tetrahedra's 24 vertexes share 12 points; internally, their eight vertexes share one point. The common center ball, being two-in-one (unity two), can be used for a pulse or a space; for an integer or a zero. The one active nucleus is the key to the binary yes-no of the invisible transistor circuitry.
1012.12 As in the 92-ball, three-frequency vector equilibrium, there are four balls to an edge going point to point with a three-space, F3, in between them. An edge of the four ball could belong either to the adjacent square or to the adjacent triangle. It cannot belong to either exclusively, and it cannot belong to them both simultaneously; it can function for either on modulated-frequency scheduling. It is like our chemical bonding, bivalent, where we get edge-to-common-edgeness.
1012.13 As shown in Numerology (Sec. 1223), when we begin to follow through the sequences of wave patterning, we discover this frequency modulation capability permeating the "Indig's" octave system of four positive, four negative, and zero nine. (See drawings section.)
Indigs of Numerology:
1 = + 1 10 = + 1 19 = + 1
2 = + 2 11 = + 2 20 = + 2
3 = + 3 12 = + 3 21 = + 3
4 = + 4 13 = +4 22 = + 4
5 = - 4 14 = - 4 23 = - 4
6 = - 3 15 = - 3 24 = - 3
7 = - 2 16 = - 2 25 = - 2
8 = - 1 17 = - 1 26 = - 1
9 = 0 18 = 0 27 = 0 Etc., etc.

Fig. 1012.14A

Fig. 1012.14B 		1012.14 Applying the Indig-Numerology to the multiplication tables, this wave phenomenon reappears dramatically, with each integer having a unique operational effect on other integers. For instance, you look at the total multiplication patterns of the prime numbers three and five and find that they make a regular X. The foumess ( = + 4) and the fiveness ( = - 4) are at the positive-negative oscillation center; they decrease and then increase on the other side where the two triangles come together with a common center in bow-tie form. You find that the sequences of octaves are so arranged that the common ball can be either number eight or it could be zero or it could be one. That is, it makes it possible for waves to run through waves without having interference of waves. (See drawings section.)

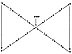Fig. 1012.15 		1012.15 Each ball can always have a neutral function among these aggregates. It is a nuclear ball whether it is in a planar array or in an omnidirectional array. It has a function in each of the two adjacent systems which performs like bonding. This is the single energy- transformative effect on closest-packed spheres which, with the arhythmical sphere space space sphere space space__suggests identity with the neutron-proton interchangeable functioning.
1012.16 The vector equilibrium as the prime convergence-divergence, i.e., gravity- radiation nucleus, provides the nuclear nothingness, the zero point where waves can go through waves without interfering with other waves. The waves are accommodated by the zeroness, by the octave of four positive and four negative phasings, and by a nuclear terminal inside-outing and a unique pattern-limit terminal outside-inning. But there are two kinds of positives and negatives: an inside-outing and an arounding. These are the additive twoness and the multiplicative twoness. The central ball then is an inside-outness and has its poles so it can accommodate either as a zeroness a wave that might go around it or go through it, without breaking up the fundamental resonance of the octaves.
1012.20 Pumping Model: The center ball of a vector equilibrium is zero. The frequency is zero, just as in the first layer the frequency is one. So zero times ten is zero; to the second power is zero; plus two is two. So the center ball has a value of two. The significance is that it has its concave and its convex. It has both insideness and outsideness congruently. It is as far as you can go. You turn yourself inside out and go in the other direction again. This is a terminal condition.
1012.21 We have then a tetrahedron that has an external and an internal: a terminal condition. Gravity converts to radiation. This is exactly why, in physics, Einstein's supposition is correct regarding the conservation of Universe: it turns around at both the maximum of expansion and the minimum of contraction, because there is clearly provided a limit and its mathematical accommodation at which it turns itself inside out.
1012.22 You get to the outside and you turn yourself outside-in; you come to the center and turn yourself inside-out. This is why radiation does not go to higher velocity. Radiation gets to a maximum and then turns itself inwardly again__it becomes gravity. Then gravity goes to its maximum concentration and turns itself and goes outwardly, becomes radiation. The zero nineness-nucleus provides the means.
Next Section: 1012.30
Copyright © 1997 Estate of R. Buckminster Fuller