400.00 SYSTEM

400.01 Definition: System

400.011 A system is the first subdivision of Universe. It divides all the Universe into six parts: first, all the universal events occurring geometrically outside the system; second, all the universal events occurring geometrically inside the system; third, all the universal events occurring nonsimultaneously, remotely, and unrelatedly prior to the system events; fourth, the Universe events occurring nonsimultaneously, remotely, and unrelatedly subsequent to the system events; fifth, all the geometrically arrayed set of events constituting the system itself; and sixth, all the Universe events occurring synchronously and or coincidentally to and with the systematic set of events uniquely considered.
400.02 A system is the first subdivision of Universe into a conceivable entity separating all that is nonsimultaneously and geometrically outside the system, ergo irrelevant, from all that is nonsimultaneously and geometrically inside and irrelevant to the system; it is the remainder of Universe that conceptually constitutes the system's set of conceptually tunable and geometrical interrelatability of events.
400.03 Conceptual tuning means occurring within the optical "rainbow" range of human's sensing within the electromagnetic spectrum and wherein the geometrical relationships are imaginatively conceivable by humans independently of size and are identifiable systematically by their agreement with the angular configurations and topological characteristics of polyhedra or polyhedral complexes.
400.04 All systems are polyhedra. Systems having insideness and outsideness must return upon themselves in a plurality of directions and are therefore interiorally concave and exteriorally convex. Because concaveness reflectively concentrates radiation impinging upon it and convexity diffuses radiation impinging upon it, concavity and convexity are fundamentally different, and therefore every system has an always and only coexisting inward and outward functionally differentialed complementarity. Any one system has only one insideness and only one outsideness.
400.05 In addition to possessing inherent insideness and outsideness, a system is inherently concave and convex, complex, and finite. A system may be either symmetrical or asymmetrical. A system may consist of a plurality of subsystems. Oneness, twoness, and threeness cannot constitute a system, as they inherently lack insideness and outsideness. Twoness constitutes wavilinear relatedness. Threeness constitutes planar relatedness, which is inherently triangular. Three triangular planes alone cannot differentiate, distinguish, or constitute a system. At minimum, it takes four triangular planes having inherent fourness of vertexes to constitute differential withinness and withoutness. Fourness of geometrically contiguous and synchronous event foci and their coincidentally defined four triangular planes, along with their six common edges provided by the six wavilinear vectors connecting the four event foci, altogether inherently differentiate, distinguish, initially institute, and constitute prime or minimum withinness and withoutness.
400.06 Thought is systemic. Cerebration and intellection are initiated by differential discernment of relevance from nonrelevance in respect to an intuitively focused-upon complex of events which also intuitively suggests inherent and potentially significant system interrelatedness.
400.07 Human thoughts are always conceptually and definitively confined to system considerability and comprehension. The whole Universe may not be conceptually considered by thought because thinkability is limited to contiguous and contemporary integrity of conformation of consideration, and Universe consists of a vast inventory of nonsynchronous, noncontiguous, noncontemporary, noncoexisting, irreversibly transforming, dissimilar events.
400.08 Unit means system integrity. Organic means regenerative system integrity. As minimum or prime systems consist of four event foci and their always and only coexisting fourness of triangularly defined planar facets, along with their sixness of a wavilinearly defined minimum set of unique componentation relatedness, unity is inherently plural. Unity is plural. A system is a local phenomenon in the Universe. Each of the conceivable or imaginable awareness or thinkability entities or phenomena inducing or producing onenesses or twonesses are subvisible and potentially further subdivisible, or as yet unresolved, ergo unrecognized systems. Functions always and only cooccur as subsystem relativistics, characteristics, inherencies, and proclivities. Functions occur only as parts of systems. Universe is constituted of a complex plurality of nonsimultaneous and only partially overlappingly occurring systems, not one system.
400.09 All the interrelationships of system foci are conceptually representable by vectors (see Sec. 521). A system is a closed configuration of vectors. It is a pattern of forces constituting a geometrical integrity that returns upon itself in a plurality of directions. Polyhedral systems display a plurality of polygonal perimeters, all of which eventually return upon themselves. Systems have an electable plurality of view-induced polarities. The polygons of polyhedra peregrinate systematically and sometimes wavilinearly around three or more noncongruent axes.
400.10 Absolutely straight lines or absolutely flat planes would, theoretically, continue onwardly or spread areally outward to infinity. The difference between infinity and finity is governed by the taking out of angular sinuses, like pieces of pie cut out of surface areas around a point in an otherwise absolute and infinitely extendable plane, and joining together the open gap's radial edges. This is the way lampshades and skirts are made. Joining the sinused fan-edges together makes a cone. If two cones are made and their respective open circle edges are brought together, a finite or closed system results. It has two poles and two polar domains. The two poles and their polar cone surface domains, as well as the defined insideness and outsideness, are inherent and primary characteristics of all systems.
400.11 All systems are continually importing as well as exporting energy. Physics has found only myriad pattern integrities of comprehensively nonsimultaneous and only partially overlapping evolution; of disintegrative "heres" and reintegrative "theres," which are omnilocal vari-intertransformabilities of limited duration identities of an apparently eternal, physical Universe regenerating mathematically treatable energy quanta.
400.20 Comprehensibility of Systems: All systems are subject to comprehension, and their mathematical integrity of topological characteristics and trigonometric interfunctioning can be coped with by systematic logic.
400.21 A system is the antithesis of a nonsystem. A nonsystem lacks omnidirectional definition. Nonsystems such as theoretical planes or straight lines cannot be found experimentally. We are scientifically bound to experientially discovered and experimentally demonstrable systems thinking.
400.22 General systems theory treats with phenomena that are holistically comprehensible. The objects of our experience are finite systems. Their superficial outlines close back upon themselves multidirectionally as a systematic continuity of relevantly contiguous events.
400.23 Maximum system complexity consists of a dissimilarly quantified inventory of unique and nonintersubstitutable components. That is, Euler's irreducible-system aspects of vertexes, areas, and edges exhibit the respective dissimilar quantities 4, 4, and 6 in the minimum prime system, the tetrahedron. This demonstrates the inherent synergy of all systems, since their minimum overall inventory of inherent characteristics is unpredicted and unpredictable by any of the parts taken separately. Systems are unpredicted by oneness, twoness, or threeness. This explains how it happens that general systems theory is a new branch of science. (See Sec. 537.30.)
400.24 General systems theory is another example of evolution by inadvertence. It developed fortuitously to accommodate the unprecedented and vastly complex undertakings of the late twentieth century, such as the 10 million separate and only partially overlapping "critical path" tasks that had to be accomplished and tested to foolproof reliability en route to countdown to eventual blastoff, Moon landing, and safe return to Earth, which found all conventional mathematical theory wanting. It required the development of the computer and star-focused instruments and computer programming arts together with operational research, which guess-improvises the inventory of parameter of variables that must be progressively programmed into the system in order further to reduce the magnitude of tolerated errors consequent to trial "bird" (rocket vehicle) "flight" (trajectory) control as the vehicles are progressively zeroed-in to progressive target rendezvous with celestial entities. Neither differential and integral calculus, nor "probability" statistics, nor any branch of specialized hard science has accredited synergy as an a priori assumption. General systems theory, which recognizes synergy as inherent, was discovered and named by the biologically inspired Ludwig von Bertalanffy.
400.25 Every system, as a subdivision of the total experience of Universe, must accommodate traffic of inbound and outbound events and inward-outward relationships with other systems' aspects of Universe. Effective thinking is systematic because intellectual comprehension occurs only when the interpatternings of experience events' star foci interrelationships return upon themselves. Then the case history becomes "closed." A system is a patterning of enclosure consisting of a conceptual aggregate of recalled experience items, or events, having inherent insideness, outsideness, and omniaroundness.
400.26 Systems are aggregates of four or more critically contiguous relevant events having neither solidity nor surface or linear continuity. Events are systemic.

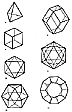Fig. 400.30 		400.30 Tiger's Skin: Typical of all finitely conceptual objects, or systems, the tiger's skin can be locally pierced and thence slotted open. Thereafter, by elongating the slot and initiating new subslots therefrom in various directions, the skin gradually can be peeled open and removed all in one piece. Adequate opening of the slots into angular sinuses will permit the skin to lie out progressively flat. Thus, the original lunar gash from the first puncture develops into many subgashes leading from the original gash into any remaining domical areas of the skin. The slitting of a paper cone from its circular edge to its apex allows the paper to be laid out as a flat "fan" intruded by an angular sinus. A sinus is the part of an angle that is not the angle's diverging sides. Sinus means in Latin a "withoutness"__an opening out__a definitively introduced "nothingness."
400.31 The surface contour of any object or system__be it the skin of a complex creature such as a crocodile, or the skin of a simple prune, or a sugar-cube wrapping, or a dodecahedron, or any formal angular polyhedra__ can thus be "skinned" and laid out flat.
400.40 Finiteness of Systems: Definition: Single systems occurring initially and minimally as four synchronously related event foci__ergo, inherently as tetrahedra, regular or irregular__are omnitriangulated and may be either symmetrical or asymmetrical. In single symmetrical systems, all the vertexes are equidistant radially from their common volumetric centers, and the centers of area of all their triangular facets are also equidistant from the system's common volumetric center.
400.41 The minimum single symmetrical system is the regular tetrahedron, which contains the least volume with the most surface as compared to all other symmetrical single systems. There are only three single symmetrical systems: the regular tetrahedron, with a "unit" volume-to-skin ratio of 1 to l; the regular octahedron, with a volume-to- surface ratio of 2 to 1; and the regular icosahedron, with a volume-to-surface ratio of 3.7 to 1. Single asymmetrical systems contain less volume per surface area of containment than do symmetrical or regular tetrahedra. The more asymmetrical, the less the volume-to- surface ratio. Since the structural strength is expressed by the vector edges, the more asymmetrical, the greater is the containment strength per unit of volumetric content.
400.42 Since the minimum system consists of two types of tetrahedra, one symmetrical (or regular) and the other asymmetrical (or irregular); and since also the asymmetrical have greater enveloping strength per units of contained event phenomena, we will differentiate the two minimum-system types by speaking of the simplest, or minimum, single symmetrical system as the mini-symmetric system; and we will refer to the minimum asymmetric system as the mini-asymmetric system. And since the mini- symmetric system is the regular tetrahedron, which cannot be compounded face-to-face with other unit-edged symmetric tetrahedra to fill allspace, but, in order to fill allspace, must be compounded with the tetrahedron's complementary symmetrical system, the octahedron, which is not a minimum system and has twice the volume-to-surface ratio of the tetrahedron of equal edge vector dimension; and since, on the other hand, two special- case minimum asymmetric tetrahedra, the A Quanta Modules and the B Quanta Modules (see Sec. 920.00), have equal volume and may be face-compounded with one another to fill allspace, and are uniquely the highest common volumetric multiple of allspace-filling; and since the single asymmetrical tetrahedron formed by compounding two symmetrical tetrahedral A Modules and one asymmetrical tetrahedral B Module will compound with multiples of itself to fill all positive space, and may be turned inside out to form its noncongruent negative complement (which may also be compounded with multiples of itself to fill all negative space), this three-module, minimum asymmetric (irregular) tetrahedral system, which accommodates both positive or negative space and whose volume is exactly 1/8 that of the regular tetrahedron; and exactly 1/32 the volume of the regular octahedron; and exactly 1/160 the volume of the regular vector equilibrium of zero frequency; and exactly 1/1280 the volume of the vector equilibrium of the initial of all frequencies, the integer 2, which is to say that, expressed in the omnirational terms of the highest common multiple allspace-filling geometry's A or B Modules, the minimum realizable nuclear equilibrium of closest-packing symmetry of unit radius spheres packed around one sphere__which is the vector equilibrium (see Sec. 413.00) __consists of 1,280 A or B Modules, and 1,280 = 28× 5.
400.43 Since the two-A-Module, one-B-Module minimum asymmetric system tetrahedron constitutes the generalized nuclear geometrical limit of rational differentiation, it is most suitably to be identified as the prime minimum rational structural system: also known as the MITE (see "Modelability," Sec. 950.00). The MITE is the mathematically demonstrable microlimit of rational fractionation of both physically energetic structuring and metaphysical structuring as a single, universal, geometrically discrete system-constant of quantation. The MITE consists of two A Modules and one B Module, which are mathematically demonstrable as the minimum cosmic volume constant, but not the geometrical shape constant. The shape differentiability renders the volume-to-surface ratio of the B Modules more envelopingly powerful than the volume-to-surface ratio of the A Modules; ergo, the most powerful local-energy-impounding, omnirationally quantatable, microcosmic structural system.
400.44 The MITE may be turned inside out by having each of its two A Modules and one B Module turn themselves inside out and recombine to fill all negative space. It is also to be observed that one all-negative-space-filling and one all-positive-space-filling MITE may be face-associated structurally to produce yet another single minimum system asymmetric tetrahedral, all-positive-and-negative space filler whose modular volumetric unity value of six corresponds with the sixness of vectorial edges of the minimum system's tetrahedral four foci event relationships.
400.45 It is characteristic of a single prime system that the aggregate of angles convergent around its vertexes must be concave or convex with respect to the position from which they are viewed__concave if viewed from the inside, convex when viewed from outside.
400.46 There are in all systems the additive twoness of the poles and the multiplicative twoness of the coexistent concavity and convexity of the system's insideness and outsideness.
400.47 Planet Earth is a system. You are a system. The "surface," or minimally enclosing envelopmental relationship, of any system such as the Earth is finite.
400.50 Other Characteristics of Systems: Prime Rational Integer Characteristics: Electromagnetic frequencies of systems are sometimes complex but always exist in complementation of gravitational forces to constitute the prime rational integer characteristics of physical systems.
400.51 Systems may be symmetrical or asymmetrical.
400.52 Systems are domains of volumes. Systems can have nuclei, and prime volumes cannot.
400.53 Interconnection of Systems: If two adjacent systems become joined by one vertex, they still constitute two systems, but universally interjointed. If two adjacent systems are interconnected by two vertexes, they remain two systems, interlocked by a hinge. If two adjacent systems become adjoined by three vertexes, they become one complex system because they have acquired unit insideness and outsideness.
400.54 If two adjacent systems are interpositioned with their respective centers of volume congruent and all their respective vertexes equidistant from their common center of volumes, they become one system. If their respective vertexes are at different distances radially from their common center of volumes, they become one complex system. If the complex system's respective interpositioned systems are all symmetric, then they become one complex symmetric system.
400.55 Polyhedra: Polyhedra consist only of polyhedra. Polyhedra are always pro tem constellations of polyhedra. Polyhedra are defined only by polyhedra and only by a minimum of four polyhedra.
400.56 All systems are polyhedra: All polyhedra are systems.
400.57 The observed or tuned-in polyhedra whose plurality of corners, faces, and edges and frequency of subdividing are tunably discernible to the tuning-in station (the observer) consist of corners that are infra-threshold-tunable polyhedra and whose faces or openings are ultra-threshold tunables.
400.60 Motion of Systems: Systems can spin. There is at least one axis of rotation of any system.
400.61 Systems can orbit. Systems can contract and expand. They can torque; they can turn inside out; and they can interprecess their parts.
400.62 Systems are, in effect, spherical gears. Their internal-external pulsating and rotating "teeth" consist in reality of both circumferential and radial waves of various frequencies of subdivision of spherical unity. They often fail to mesh with other local systems. Some of them mesh only in special aspects. The universally frequent nonmeshing of geometrical sizes and rates of wavelengths and frequencies produces an omnicondition in which the new system's center, as each is created, must continually occupy an omnidirectionally greater domain.
Next Section: 400.65
Copyright © 1997 Estate of R. Buckminster Fuller