Volumetric Variability with Topological Constancy
|
|
936.00
Volumetric Variability with Topological Constancy
|
|
|
936.10
Symmetrical and Asymmetrical Contraction
|
|
|
936.11
An octahedron consists of 12 vector edges and two
units of quantum and has
a volume of four when the tetrahedron is taken as unity.
(See Table
223.64.) Pulling two
ends of a rope in opposite directions makes the rope's
girth contract precessionally in a
plane at 90 degrees to the axis of purposeful tensing.
(Sec.
1054.61.) Or if we push
together the opposite sides of a gelatinous mass or
a pneumatic pillow, the gelatinous
mass or the pneumatic pillow swells tensively outward
in a plane at 90 degrees to the line
of our purposeful compressing. This 90-degree reaction__or
resultant__is characteristic of
precession. Precession is the effect of bodies in motion
upon other bodies in motion. The
gravitational pull of the Sun on the Earth makes the
Earth go around the Sun in an orbit at
degrees to the line of the Earth-Sun gravitational
interattraction. The effect of the
Earth on the Moon or of the nucleus of the atom upon
its electron is to make these
interattractively dependent bodies travel in orbits
at 90 degrees to their mass-
interattraction force lines.
|
 Fig. 936.12 |
936.12
The octahedron represents the most commonly occurring
crystallographic
conformation in nature. (See Figs.
931.10
and
1054.40.)
It is the most typical association
of energy-as-matter; it is at the heart of such association.
Any focused emphasis in the
gravitational pull of the rest of the Universe upon
the octahedron's symmetry precesses it
into asymmetrical deformation in a plane at 90 degrees
to the axis of exaggerated pulling.
This forces one of the 12 edge vectors of the octahedron
to rotate at 90 degrees. If we
think of the octahedron's three XYZ axes and its six
vertexes, oriented in such a manner
that X is the north pole and X' is the south pole, the
other four vertexes__Y, Z, Y', Z'__all
occur in the plane of, and define, the octahedron's
equator. The effect of gravitational pull
upon the octahedron will make one of the four equatorial
vectors disengage from its two
adjacent equatorial vertexes, thereafter to rotate 90
degrees and then rejoin its two ends
with the north pole and south pole vertexes. (See Fig.
936.12 and color plate 6.)
|
|
|
936.13
When this precessional transformation is complete,
we have the same
topological inventories of six vertexes, eight exterior
triangular faces, and 12 vector edges
as we had before in the symmetrical octahedron; but
in the process the symmetrical, four-
tetrahedra-quanta-volume octahedron has been transformed
into three tetrahedra (three-
quanta volume) arranged in an arc section of an electromagnetic
wave conformation with
each of the two end tetrahedra being face bonded to
the center tetrahedron. (See Sec. 982.73)
|
|
|
936.14
The precessional effect has been to rearrange the
energy vectors themselves
in such a way that we have gone from the volume-four
quanta of the symmetrical
octahedron to the volume-three quanta of the asymmetric
tetra-arc-array segment of an
electromagnetic wave pattern. Symmetric matter has been
entropically transformed into
asymmetrical and directionally focused radiation: one
quantum of energy has seemingly
disappeared. When the radiation impinges interferingly
with any other energy event in
Universe, precession recurs and the three-quantum electromagnetic
wave retransforms
syntropically into the four-quantum octahedron of energy-as-matter.
And vice versa.
Q.E.D. (See Fig. 936.14.)
|
|
|
936.15
The octahedron goes from a volume of four to a volume
of three as one
tensor is precessed at 90 degrees. This is a demonstration
in terms of tension and
compression of how energy can disappear and reappear.
The process is reversible, like
Boltzmann's law and like the operation of syntropy and
entropy. The lost tetrahedron can
reappear and become symmetrical in its optimum form
as a ball-bearing-sphere
octahedron. There are six great circles doubled up in
the octahedron. Compression is
radiational: it reappears. Out of the fundamental fourness
of all systems we have a model
of how four can become three in the octahedron conservation
and annihilation model.
|
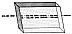 Fig. 936.16 |
936.16
See the Iceland spar crystals for the octahedron's
double vector-edge image.
|
|
|
936.17
The interior volume of the concave-vector-equilibrium-shaped
space
occurring interiorly between the six uniradius octahedral
collection of closest-packed
spheres is greater than is the concave-octahedrally-shaped
space occurring interiorly
between the four uniradius tetrahedral collection of
closest-packed spheres, which
tetrahedral collection constitutes the minimum structural
system in Universe, and its
interior space is the minimum interior space producible
within the interstices of closest-
packed uniradius spheres.
|
|
|
936.18
Thus the larger interior space within the omnitriangularly
stable, six-vertex-
ball, 12-vector-edge octahedron is subject to volumetric
compressibility. Because its
interior space is not minimal, as the octahedron is
omniembracingly tensed gravitationally
between any two or more bodies, its six balls will tend
precessionally to yield
transformingly to produce three closest-packed, uniradius,
sphere-vertex-defined, face-
bonded tetrahedra.
|
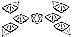 Fig. 936.19 |
936.19
As we tense the octahedron, it strains until one vector
(actually a double, or
unity-as-two, vector) yields its end bondings and precesses
at 90 degrees to transform the
system into three double-bonded (face-bonded) tetrahedra
in linear arc form. This tetra-
arc, embryonic, electromagnetic wave is in neutral phase.
The seemingly annihilated__but
in fact only separated-out-quantum is now invisible
because vectorless. It now becomes
invisibly face-bonded as one invisible tetrahedron.
The separated-out quantum is face-
bonded to one of the furthermost outward triangular
faces occurring at either end of the
tetra-arc array of three (consisting of one tetra at
the middle with each of the two adjacent
tetra face-bonded to it); the fourth invisible tetrahedron
is face-bonded to one or the other
of the two alternatively vacant, alternatively available
furthermost end faces of the tetra-
arc group. With this fourth, invisible tetrahedral addition
the overall triple-bonded
tetrahedral array becomes either rightwardly or leftwardly
spiraled to produce a four-
tetrahedron tetrahelix, which is a potential, event
embryo, electromagnetic-circuitry gap
closer. Transmission may thereafter be activated as
a connected chain of the inherently
four-membered, individual-link continuity. This may
explain the dilemma of the wave vs
the particle. (See Sec.
973.30, Fig.
936.19, and color
plates 6 and 7.)
|
|
|
936.20
Conceptual Conservation and Annihilation
|
|
|
936.21
The octahedron as the conservation and annihilation
model provides an
experiential and conceptual accounting for the question:
What happens to entropically
vanishing quanta of energy that have never been identified
as discretely lost when new
quanta appeared elsewhere and elsewhen? Were these appearing
and disappearing quanta
being encountered for the first time as we became capable
of penetrating exploration of
ever vaster ranges of Universe?
|
|
|
936.22
Boltzmann hypothesized and Einstein supported his
working
assumption__stated in the conceptual language of synergetics__that
there can be no a
priori stars to radiate entropically and visibly to
the information-importing, naked eyes of
Earthian humans (or to telescopes or phototelescopy
or electromagnetic antennae) if there
were not also invisible cosmic importing centers. The
importing centers are invisible
because they are not radiantly exporting; they are in
varying stages of progressive
retrieving, accumulating, sorting, storing, and compressing
energies. The cosmic
abundance of the myriads of such importing centers and
their cosmic disposition in
Scenario Universe exactly balances and conserves the
integrity of eternally regenerative
Universe.
|
|
|
936.23
In Scenario Universe (in contrast to a spherically-structured,
normally-at-
rest, celestially-concentric, single-frame-picture Universe)
the episodes consist only of
such frequencies as are tune-in-able by the limited-frequency-range
set of the viewer.
|
|
|
936.24
There is no such phenomenon as space: there is only
the at-present-tuned-in
set of relationships and the untuned intervalling. Points
are twilight-border-line, only
amplitude-tuned-in (AM), directionally oriented, static
squeaks or pips that, when
frequency-tuned (FM), become differentially discrete
and conceptually resolvable as
topological systems having withinness and withoutness__ergo,
at minimum having four
corner-defining yet subtunable system pips or point-to-able
corner loci. In systemic cosmic
topology Euler's vertexes (points) are then always only
twilight energy-event loci whose
discrete frequencies are untunable at the frequency
range of the reception set of the
observer.
|
|
|
937.00
Geometry and Number Share the Same Model
|
|
|
937.10
Midway Between Limits
|
|
|
937.11
The grand strategy of quantum mechanics may be described
as progressive,
numerically rational fractionating of the limit of total
energy involved in eternally
regenerative Universe.
|
|
|
937.12
When seeking a model for energy quanta conservation
and annihilation, we
are not surprised to find it in the middle ranges of
the geometrical hierarchy of prime
structural systems__tetrahedron, octahedron, and icosahedron
(see Sec.
610.20). The
tetrahedron and icosahedron are the two extreme and
opposite limit cases of symmetrical
structural systems: they are the minimum-maximum cosmic
limits of such prime structures
of Universe. The octahedron ranks in the neutral area,
midway between the extremes.
|
|
|
937.13
The prime number characteristic of the tetrahedron
is 1; the prime number
characteristic of the icosahedron is 5. Both of these
prime numbers__1 and 5__are odd
numbers, in contradistinction to the prime number characteristic
of the middle-case
structural-system octahedron, which is 2, an even number
and the only even numbered
prime number. Again, we are not surprised to find that
the octahedron is the most
common crystal conformation in nature.
|
|
|
937.14
The tetrahedron has three triangles around each vertex;
the octahedron has
four; and the icosahedron has five. The extreme-limit
cases of structural systems are
vertexially locked by odd numbers of triangular gears,
while the vertexes of the
octahedron at the middle range have an even number of
reciprocating triangular gears.
This shows that the octahedron's three great circles
are congruent pairs__i.e., six circles
that may seem to appear as only three, which quadrivalent
doubling with itself is clearly
shown in the jitterbug model, where the 24 vector edges
double up at the octahedron
phase to produce 12 double-congruent vector edges and
thus two congruent octahedra.
(See Fig. 460.08D.)
|
|
|
937.15
The octahedron is doubled-up in the middle range of
the vector equilibrium's
jitterbug model; thus it demonstrates conceptually the
exact middle between the macro-
micro limits of the sequence of intertransformative
events. The octahedron in the middle
of the structural-system hierarchy provides us with
a clear demonstration of how a unit
quantum of energy seemingly disappears__i.e., becomes
annihilated__and vice versa.
|
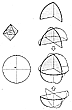 Fig. 937.20 |
937.20
Doubleness of Octahedron
|
|
|
937.21
The octahedron always exhibits the quality of doubleness.
When the
octahedron first appears in the symmetrical contraction
of the vector equilibrium jitterbug
system, it appears with all of its vectors doubled (see
Fig. 460.08D 460.08D).
It also takes two sets
of three great circles each to fold the octahedron.
You might think you could do it with
one set of three great circles, but the foldability
of the octahedron requires two sets of
three great circles each. (See Secs.
835
and
836.) There
are always six great circles
doubled up in the octahedron to reappear only as three.
(See Fig.
937.20.)
|
|
|
937.22
And we also recall that the octahedron appears as
the prime number 2 in the
geometrical hierarchy, while its volume is 4 when the
tetrahedron is taken as volumetric
units (see Table
223.64).
1, 4, 3, 6, 18.51, and 20.
|
|
|
937.30
Octahedron as Sphere of Compression
|
|
|
937.31
The slenderness ratio in gravitationally tensed functioning
has no minimum
overall limit of its structural-system length, as compared
to the diameter of the system's
midlength cross section; ergo,
|
| Next Section: 938.00 |