
 Consideration 13: Correspondence of Surface Angles
and Central Angles
Consideration 13: Correspondence of Surface Angles
and Central Angles

|
986.480  Consideration 13: Correspondence of Surface Angles
and Central Angles
Consideration 13: Correspondence of Surface Angles
and Central Angles
|

|
986.481
 It was next to be noted that spherical trigonometry
shows that nature's
smallest common denominator of system-surface subdivisioning
by any one type of the
seven great-circle-symmetry systems is optimally accomplished
by the previously
described 120 spherical-surface triangles formed by
the 15 great circles, whose central
angles are approximately
It was next to be noted that spherical trigonometry
shows that nature's
smallest common denominator of system-surface subdivisioning
by any one type of the
seven great-circle-symmetry systems is optimally accomplished
by the previously
described 120 spherical-surface triangles formed by
the 15 great circles, whose central
angles are approximately
|

|
986.482
 We recall that the further self-subdividing of the
120 triangles, as already
defined by the 15 great circles and as subdividingly
accomplished by the icosahedron's
additional 6- and 10-great-circle spinnabilities, partitions
the 120 LCD triangles into 480
right triangles of four types: ADC, CDE, CFE, and EFB-with
60 positive and 60 negative
pairs of each. (See Figs.
901.03
and
986.314.) We also
recall that the 6- and 10-great-
circle-spun hemispherical gridding further subdivided
the 120 right
triangles__ACB__formed by the 15 great circles, which
produced a total of 12 types of
surface angles, four of them of 90 degrees, and three
whose most acute angles subdivided
the 90-degree angle at C into three surface angles:
ACD__31.7 degrees; DCE__37.4
degrees; and ECB__20.9 degrees, which three surface angles,
we remember, correspond
exactly to the three central angles COB, BOA, and COA,
respectively, of the
triacontahedron's tetrahedral T Quanta Module ABCOt.
We recall that the further self-subdividing of the
120 triangles, as already
defined by the 15 great circles and as subdividingly
accomplished by the icosahedron's
additional 6- and 10-great-circle spinnabilities, partitions
the 120 LCD triangles into 480
right triangles of four types: ADC, CDE, CFE, and EFB-with
60 positive and 60 negative
pairs of each. (See Figs.
901.03
and
986.314.) We also
recall that the 6- and 10-great-
circle-spun hemispherical gridding further subdivided
the 120 right
triangles__ACB__formed by the 15 great circles, which
produced a total of 12 types of
surface angles, four of them of 90 degrees, and three
whose most acute angles subdivided
the 90-degree angle at C into three surface angles:
ACD__31.7 degrees; DCE__37.4
degrees; and ECB__20.9 degrees, which three surface angles,
we remember, correspond
exactly to the three central angles COB, BOA, and COA,
respectively, of the
triacontahedron's tetrahedral T Quanta Module ABCOt.
|

|
986.500
 E Quanta Module
E Quanta Module
|

|
986.501
 Consideration 14: Great-circle Foldable Discs
Consideration 14: Great-circle Foldable Discs
|
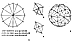 Fig. 986.502 |
986.502
 With all the foregoing events, data, and speculative
hypotheses in mind, I
said I think it would be worthwhile to take 30 cardboard
great circles, to divide them into
four 90-degree quadrants, then to divide each of the
quadrants into three angles__COA,
20.9 degrees; AOB, 37.4 degrees; and BOC, 31.7 degrees__and
then to score the
cardboard discs with fold lines in such a manner that
the four lines CO will be negatively
outfolded, while the lines AO and BO will be positively
infolded, so that when they are
altogether folded they will form four similar-arc-edged
tetrahedra ABCO with all of their
four CO radii edges centrally congruent. And when 30
of these folded great-circle sets of
four T Quanta Module tetrahedra are each triple-bonded
together, they will altogether
constitute a sphere. This spherical assemblage involves
pairings of the three intercongruent
interface triangles AOC, COB, and BOA; that is, each
folded great-circle set of four tetra
has each of its four internal triangular faces congruent
with their adjacent neighbor's
corresponding AOC, COB, and BOC interior triangular
faces. (See Fig.
986.502.)
With all the foregoing events, data, and speculative
hypotheses in mind, I
said I think it would be worthwhile to take 30 cardboard
great circles, to divide them into
four 90-degree quadrants, then to divide each of the
quadrants into three angles__COA,
20.9 degrees; AOB, 37.4 degrees; and BOC, 31.7 degrees__and
then to score the
cardboard discs with fold lines in such a manner that
the four lines CO will be negatively
outfolded, while the lines AO and BO will be positively
infolded, so that when they are
altogether folded they will form four similar-arc-edged
tetrahedra ABCO with all of their
four CO radii edges centrally congruent. And when 30
of these folded great-circle sets of
four T Quanta Module tetrahedra are each triple-bonded
together, they will altogether
constitute a sphere. This spherical assemblage involves
pairings of the three intercongruent
interface triangles AOC, COB, and BOA; that is, each
folded great-circle set of four tetra
has each of its four internal triangular faces congruent
with their adjacent neighbor's
corresponding AOC, COB, and BOC interior triangular
faces. (See Fig.
986.502.)
|

|
986.503
 I proceeded to make 30 of these 360-degree-folding
assemblies and used
bobby pins to lock the four CO edges together at the
C centers of the diamond-shaped
outer faces. Then I used bobby pins again to lock the
30 assemblies together at the 20
convergent A vertexes and the 12 convergent B sphere-surface
vertexes. Altogether they
made a bigger sphere than the calculated radius, because
of the accumulated thickness of
the foldings of the construction paper's double-walled
(trivalent) interfacing of the 30
internal tetrahedral components. (See Fig.
986.502D.)
I proceeded to make 30 of these 360-degree-folding
assemblies and used
bobby pins to lock the four CO edges together at the
C centers of the diamond-shaped
outer faces. Then I used bobby pins again to lock the
30 assemblies together at the 20
convergent A vertexes and the 12 convergent B sphere-surface
vertexes. Altogether they
made a bigger sphere than the calculated radius, because
of the accumulated thickness of
the foldings of the construction paper's double-walled
(trivalent) interfacing of the 30
internal tetrahedral components. (See Fig.
986.502D.)
|
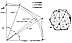 Fig. 986.504 |
986.504
 Instead of the just previously described 30 assemblies
of four identical
spherically central tetrahedra, each with all of their
62 vertexes in the unit-radius spheres, I
next decided to make separately the 120 correspondingly
convergent (non-arc-edged but
chorded) tetrahedra of the tetravolume-5 rhombic triacontahedron,
with its 30 flat ABAB
diamond faces, the center C of which outer diamond faces
is criss-crossed at right angles
at C by the short axis A-A of the diamond and by its
long axis B-B, all of which diamond
bounding and criss-crossing is accomplished by the same
15 greatcircle planes that also
described the 30 diamonds' outer boundaries. As noted,
the criss-crossed centers of the
diamond faces occur at C, and all the C points are at
the prime-vector-radius distance
outwardly from the volumetric center O of the rhombic
triacontahedron, while OA is 1.07
of vector unity and OB is 1.17 of vector unity outward,
respectively, from the rhombic
triacontahedron's symmetrical system's center of volume
O. (See Figs.
986.504A and
986.504B.)
Instead of the just previously described 30 assemblies
of four identical
spherically central tetrahedra, each with all of their
62 vertexes in the unit-radius spheres, I
next decided to make separately the 120 correspondingly
convergent (non-arc-edged but
chorded) tetrahedra of the tetravolume-5 rhombic triacontahedron,
with its 30 flat ABAB
diamond faces, the center C of which outer diamond faces
is criss-crossed at right angles
at C by the short axis A-A of the diamond and by its
long axis B-B, all of which diamond
bounding and criss-crossing is accomplished by the same
15 greatcircle planes that also
described the 30 diamonds' outer boundaries. As noted,
the criss-crossed centers of the
diamond faces occur at C, and all the C points are at
the prime-vector-radius distance
outwardly from the volumetric center O of the rhombic
triacontahedron, while OA is 1.07
of vector unity and OB is 1.17 of vector unity outward,
respectively, from the rhombic
triacontahedron's symmetrical system's center of volume
O. (See Figs.
986.504A and
986.504B.)
|
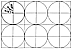 Fig. 986.505 |
986.505
 To make my 120 OABC tetrahedra I happened to be using
the same
construction paperboard I had used before in making
the 30 arc-edged great-circle
components. The construction paperboard happened to
come in sheets 24 by 36 inches,
i.e., two feet by three feet. In making the previously
described spherical triacontahedron
out of these 24-by-36-inch sheets, I had decided to
get the most out of my material by
using a 12-inch-diameter circle, so that I could lay
out six of them tangentially within the
six 12-inch-square modules of the paperboard to produce
the 30 foldable great circles.
This allowed me to cut out six intertangent great circles
from each 24-by-36-inch
construction paper sheet. Thirty great circles required
only five sheets, each sheet
producing six circles. To make the 12 separate T Quanta
Module tetrahedra, I again
spontaneously divided each of the same-size sheets into
six squares with each of the six
circles tangent to four edges of each square (Fig.
986.505).
To make my 120 OABC tetrahedra I happened to be using
the same
construction paperboard I had used before in making
the 30 arc-edged great-circle
components. The construction paperboard happened to
come in sheets 24 by 36 inches,
i.e., two feet by three feet. In making the previously
described spherical triacontahedron
out of these 24-by-36-inch sheets, I had decided to
get the most out of my material by
using a 12-inch-diameter circle, so that I could lay
out six of them tangentially within the
six 12-inch-square modules of the paperboard to produce
the 30 foldable great circles.
This allowed me to cut out six intertangent great circles
from each 24-by-36-inch
construction paper sheet. Thirty great circles required
only five sheets, each sheet
producing six circles. To make the 12 separate T Quanta
Module tetrahedra, I again
spontaneously divided each of the same-size sheets into
six squares with each of the six
circles tangent to four edges of each square (Fig.
986.505).
|

|
986.506
 In starting to make the 120 separate tetrahedra (60
positive, 60
negative__known as T Quanta Modules) with which to assemble
the triacontahedron-
which is a chord-edged polyhedron vs the previous "spherical"
form produced by the
folded 15-great-circle patterning__I drew the same 12-inch-edge
squares and, tangentially
within the latter, drew the same six 12-inch-diameter
circles on the five 24-by-36-inch
sheets, dividing each circle into four quadrants and
each quadrant into three subsections of
20.9 degrees, 37.4 degrees, and 31.7 degrees, as in
the T Quanta Modules.
In starting to make the 120 separate tetrahedra (60
positive, 60
negative__known as T Quanta Modules) with which to assemble
the triacontahedron-
which is a chord-edged polyhedron vs the previous "spherical"
form produced by the
folded 15-great-circle patterning__I drew the same 12-inch-edge
squares and, tangentially
within the latter, drew the same six 12-inch-diameter
circles on the five 24-by-36-inch
sheets, dividing each circle into four quadrants and
each quadrant into three subsections of
20.9 degrees, 37.4 degrees, and 31.7 degrees, as in
the T Quanta Modules.
|

|
986.507
 I planned that each of the quadrants would subsequently
be cut from the
others to be folded into one each of the 120 T Quanta
Module tetrahedra of the
triacontahedron. This time, however, I reminded myself
not only to produce the rhombic
triacontahedron with the same central angles as in the
previous spheric experiment's
model, but also to provide this time for surfacing their
clusters of four tetrahedra ABCO
around their surface point C at the mid-crossing point
of their 30 flat diamond faces. Flat
diamond faces meant that where the sets of four tetra
came together at C, there would not
only have to be four 90-degree angles on the flat surface,
but there would be eight internal
right angles at each of the internal flange angles.
This meant that around each vertex C
corner of each of the four T Quanta Modules OABC coming
together at the diamond face
center C there would have to be three 90-degree angles.
I planned that each of the quadrants would subsequently
be cut from the
others to be folded into one each of the 120 T Quanta
Module tetrahedra of the
triacontahedron. This time, however, I reminded myself
not only to produce the rhombic
triacontahedron with the same central angles as in the
previous spheric experiment's
model, but also to provide this time for surfacing their
clusters of four tetrahedra ABCO
around their surface point C at the mid-crossing point
of their 30 flat diamond faces. Flat
diamond faces meant that where the sets of four tetra
came together at C, there would not
only have to be four 90-degree angles on the flat surface,
but there would be eight internal
right angles at each of the internal flange angles.
This meant that around each vertex C
corner of each of the four T Quanta Modules OABC coming
together at the diamond face
center C there would have to be three 90-degree angles.
|
 Fig. 986.508 |
986.508
 Looking at my "one-circle-per-each-of-six-squares"
drawing, I saw that each
sheet was divided into 24 quadrant blanks, as in Fig.
986.508A986.508A.
Next I marked the centers
of each of the six circles as point O, O being the volumetric
center of the triacontahedral
system. Then I realized that, as trigonometrically calculated,
the flat, diamond-centered,
right-angled, centrally criss-crossed point C of the
triacontahedron's outer faces had to be
at our primitive unit-vector-length distance outwardly
from the system center O, whereas
in the previous arc-edged 30-great-circle-folded model
the outer vertex C had been at full-
spherical-system-radius distance outwardly from O. In
the spherical 15-great-circle-model,
therefore, the triacontahedron's mid-flat-diamond-face
C would be at 0.07 lesser radial
distance outwardly from O than would the diamond corner
vertexes A and vertex A itself
at a lesser radial distance outwardly from O than diamond
corner vertex B. (See Fig.
986.504A.)
Looking at my "one-circle-per-each-of-six-squares"
drawing, I saw that each
sheet was divided into 24 quadrant blanks, as in Fig.
986.508A986.508A.
Next I marked the centers
of each of the six circles as point O, O being the volumetric
center of the triacontahedral
system. Then I realized that, as trigonometrically calculated,
the flat, diamond-centered,
right-angled, centrally criss-crossed point C of the
triacontahedron's outer faces had to be
at our primitive unit-vector-length distance outwardly
from the system center O, whereas
in the previous arc-edged 30-great-circle-folded model
the outer vertex C had been at full-
spherical-system-radius distance outwardly from O. In
the spherical 15-great-circle-model,
therefore, the triacontahedron's mid-flat-diamond-face
C would be at 0.07 lesser radial
distance outwardly from O than would the diamond corner
vertexes A and vertex A itself
at a lesser radial distance outwardly from O than diamond
corner vertex B. (See Fig.
986.504A.)
|

|
986.509
 Thinking about the C corner of the described tetrahedron
consisting entirely
of 90-degree angles as noted above, I realized that
the line C to A must produce a 90-
degree-angle as projected upon the line OC", which latter
ran vertically outward from O
to C", with O being the volumetric center of the symmetrical
system (in this case the
rhombic triacontahedron) and with C" positioned on the
perimeter exactly where vertex C
had occurred on each of the previous arc-described models
of the great circles as I had
laid them out for my previous 15 great-circle spherical
models. I saw that angle ACO must
be 90 degrees. I also knew by spherical trigonometry
that the angle AOC would have to be
20.9 degrees, so I projected line OA outwardly from
O at 20.9 degrees from the vertical
square edge OC.
Thinking about the C corner of the described tetrahedron
consisting entirely
of 90-degree angles as noted above, I realized that
the line C to A must produce a 90-
degree-angle as projected upon the line OC", which latter
ran vertically outward from O
to C", with O being the volumetric center of the symmetrical
system (in this case the
rhombic triacontahedron) and with C" positioned on the
perimeter exactly where vertex C
had occurred on each of the previous arc-described models
of the great circles as I had
laid them out for my previous 15 great-circle spherical
models. I saw that angle ACO must
be 90 degrees. I also knew by spherical trigonometry
that the angle AOC would have to be
20.9 degrees, so I projected line OA outwardly from
O at 20.9 degrees from the vertical
square edge OC.
|

|
986.510
 At the time of calculating the initial layout I made
two mistaken
assumptions: first, that the 0.9995 figure was critically
approximate to 1 and could be read
as 1; and second (despite Chris Kitrick's skepticism
born of his confidence in the reliability
of his calculations), that the 0.0005 difference must
be due to the residual
incommensurability error of the inherent irrationality
of the mathematicians' method of
calculating trigonometric functions. (See the Scheherazade
Numbers discussed at Sec.
1230.)
At any rate I could not lay out with drafting
tools a difference of 0.0005 of six
inches, which is 0.0030 of an inch. No draftsman can
prick off a distance even ten times
that size. (I continue to belabor these mistaken assumptions
and the subsequent
acknowledgments of the errors because it is always upon
the occasion of my enlightened
admission of error that I make my greatest discoveries,
and I am thus eager to convey this
truth to those seeking the truth by following closely
each step of this development, which
leads to one of the most exciting of known discoveries.)
At the time of calculating the initial layout I made
two mistaken
assumptions: first, that the 0.9995 figure was critically
approximate to 1 and could be read
as 1; and second (despite Chris Kitrick's skepticism
born of his confidence in the reliability
of his calculations), that the 0.0005 difference must
be due to the residual
incommensurability error of the inherent irrationality
of the mathematicians' method of
calculating trigonometric functions. (See the Scheherazade
Numbers discussed at Sec.
1230.)
At any rate I could not lay out with drafting
tools a difference of 0.0005 of six
inches, which is 0.0030 of an inch. No draftsman can
prick off a distance even ten times
that size. (I continue to belabor these mistaken assumptions
and the subsequent
acknowledgments of the errors because it is always upon
the occasion of my enlightened
admission of error that I make my greatest discoveries,
and I am thus eager to convey this
truth to those seeking the truth by following closely
each step of this development, which
leads to one of the most exciting of known discoveries.)
|

|
986.511
 In order to produce the biggest model possible out
of the same 24-by-36-
inch construction paper blanks, I saw that vertex A
of this new T Quanta Module model
would have to lie on the same 12-inch circle, projecting
horizontally from A
perpendicularly (i.e., at right angles), upon OX at
C. I found that the point of 90-degree
impingement of AC on OX occurred slightly inward (0.041,
as we learned later
by/trigonometry), vertically inward, from X. The symbol
X now occurs on my layout at the
point where the previous spherical model's central diamond
vertex C had been
positioned__-on the great-circle perimeter. Trigonometric
calculation showed this
distance between C and X to be 0.041 of the length of
our unit vector radius. Because (1)
the distance CO is established by the right-angled projection
of A upon OX; and because
(2) the length CO is also the prime vector of synergetics'
isotropic vector matrix itself, we
found by trigonometric calculation that when the distance
from O to C is 0.9995 of the
prime vector's length, that the tetravolume of the rhombic
triacontahedron is exactly 5.
In order to produce the biggest model possible out
of the same 24-by-36-
inch construction paper blanks, I saw that vertex A
of this new T Quanta Module model
would have to lie on the same 12-inch circle, projecting
horizontally from A
perpendicularly (i.e., at right angles), upon OX at
C. I found that the point of 90-degree
impingement of AC on OX occurred slightly inward (0.041,
as we learned later
by/trigonometry), vertically inward, from X. The symbol
X now occurs on my layout at the
point where the previous spherical model's central diamond
vertex C had been
positioned__-on the great-circle perimeter. Trigonometric
calculation showed this
distance between C and X to be 0.041 of the length of
our unit vector radius. Because (1)
the distance CO is established by the right-angled projection
of A upon OX; and because
(2) the length CO is also the prime vector of synergetics'
isotropic vector matrix itself, we
found by trigonometric calculation that when the distance
from O to C is 0.9995 of the
prime vector's length, that the tetravolume of the rhombic
triacontahedron is exactly 5.
|

|
986.512
 When the distance from O to C is 0.9995, then the tetravolume
of the
rhombic triacontahedron is exactly 5. OC in our model
layout is now exactly the same as
the vector radius of the isotropic vector matrix of
our "generalized energy field." OC rises
vertically (as the right-hand edge of our cut-out model
of our eventually-to-be-folded T
Quanta Module's model designing layout) from the eventual
triacontahedron's center O to
what will be the mid-diamond face point C. Because by
spherical trigonometry we know
that the central angles of our model must read successively
from the right-hand edge of
the layout at 20.9 degrees, 37.4 degrees, and 31.7 degrees
and that they add up to 90
degrees, therefore line OC' runs horizontally leftward,
outward from O to make angle
COC' 90 degrees. This is because all the angles around
the mid-diamond criss-cross point
C are (both externally and internally) 90 degrees. We
also know that horizontal OC' is the
same prime vector length as vertical OC. We also know
that in subsequent folding into the
T Quanta Module tetrahedron, it is a mathematical requirement
that vertical OC be
congruent with horizontal OC' in order to be able to
have these edges fold together to be
closed in the interior tetrahedral form of the T Quanta
Module. We also know that in
order to produce the required three 90-degree angles
(one surface and two interior)
around congruent C and C' of the finished T Quanta Module,
the line C'B of our layout
must rise at 90 degrees vertically from C' at the leftward
end of the horizontal unit vector
radius OC'. (See Fig.
986.508C.)
When the distance from O to C is 0.9995, then the tetravolume
of the
rhombic triacontahedron is exactly 5. OC in our model
layout is now exactly the same as
the vector radius of the isotropic vector matrix of
our "generalized energy field." OC rises
vertically (as the right-hand edge of our cut-out model
of our eventually-to-be-folded T
Quanta Module's model designing layout) from the eventual
triacontahedron's center O to
what will be the mid-diamond face point C. Because by
spherical trigonometry we know
that the central angles of our model must read successively
from the right-hand edge of
the layout at 20.9 degrees, 37.4 degrees, and 31.7 degrees
and that they add up to 90
degrees, therefore line OC' runs horizontally leftward,
outward from O to make angle
COC' 90 degrees. This is because all the angles around
the mid-diamond criss-cross point
C are (both externally and internally) 90 degrees. We
also know that horizontal OC' is the
same prime vector length as vertical OC. We also know
that in subsequent folding into the
T Quanta Module tetrahedron, it is a mathematical requirement
that vertical OC be
congruent with horizontal OC' in order to be able to
have these edges fold together to be
closed in the interior tetrahedral form of the T Quanta
Module. We also know that in
order to produce the required three 90-degree angles
(one surface and two interior)
around congruent C and C' of the finished T Quanta Module,
the line C'B of our layout
must rise at 90 degrees vertically from C' at the leftward
end of the horizontal unit vector
radius OC'. (See Fig.
986.508C.)
|

|
986.513
 This layout now demonstrates three 90-degree comers
with lines OC vertical
and OC' horizontal and of the same exact length, which
means that the rectangle COC'C"
must be a square with unit-vector-radius edge length
OC. The vertical line C'C" rises
from C' of horizontal OC' until it encounters line OB,
which__to conform with the
triacontahedron's interior angles as already trigonometrically
established__must by angular
construction layout run outwardly from O at an angle
of 31.7 degrees above the horizontal
from OC' until it engages vertical C'C" at B. Because
by deliberate construction
requirement the angle between vertical OC and OA has
been laid out as 20.9 degrees, the
angle AOB must be 37.4 degrees-being the remainder after
deducting both 20.9 degrees
and 31.7 degrees from the 90-degree angle Lying between
vertical OC and horizontal
OC'. All of this construction layout with OC' horizontally
equaling OC vertically, and
with the thus-far-constructed layout's corner angles
each being 90 degrees, makes it
evident that the extensions of lines CA and C'B will
intersect at 90 degrees at point C",
thus completing the square OC `C"C of edge length OC,
which length is exactly
0.999483332 of the prime vector of the isotropic vector
matrix's primitive cosmic-
hierarchy system.
This layout now demonstrates three 90-degree comers
with lines OC vertical
and OC' horizontal and of the same exact length, which
means that the rectangle COC'C"
must be a square with unit-vector-radius edge length
OC. The vertical line C'C" rises
from C' of horizontal OC' until it encounters line OB,
which__to conform with the
triacontahedron's interior angles as already trigonometrically
established__must by angular
construction layout run outwardly from O at an angle
of 31.7 degrees above the horizontal
from OC' until it engages vertical C'C" at B. Because
by deliberate construction
requirement the angle between vertical OC and OA has
been laid out as 20.9 degrees, the
angle AOB must be 37.4 degrees-being the remainder after
deducting both 20.9 degrees
and 31.7 degrees from the 90-degree angle Lying between
vertical OC and horizontal
OC'. All of this construction layout with OC' horizontally
equaling OC vertically, and
with the thus-far-constructed layout's corner angles
each being 90 degrees, makes it
evident that the extensions of lines CA and C'B will
intersect at 90 degrees at point C",
thus completing the square OC `C"C of edge length OC,
which length is exactly
0.999483332 of the prime vector of the isotropic vector
matrix's primitive cosmic-
hierarchy system.
|

|
986.514
 Since ACO, COC', and OC'B are all 90-degree angles,
and since vertical CO
= horizontal C'O in length, the area COC'C" must be
a square. This means that two edges
of each of three of the four triangular faces of the
T Quanta Module tetrahedron, and six
of its nine prefolded edges (it has only six edges after
folding), are congruent with an
exactly square paperboard blank. The three triangles
OCA, OAB, and OBC' will be folded
inwardly along AO and BO to bring the two CO and CO'
edges together to produce the
three systemically interior faces of the T Quanta Module.
Since ACO, COC', and OC'B are all 90-degree angles,
and since vertical CO
= horizontal C'O in length, the area COC'C" must be
a square. This means that two edges
of each of three of the four triangular faces of the
T Quanta Module tetrahedron, and six
of its nine prefolded edges (it has only six edges after
folding), are congruent with an
exactly square paperboard blank. The three triangles
OCA, OAB, and OBC' will be folded
inwardly along AO and BO to bring the two CO and CO'
edges together to produce the
three systemically interior faces of the T Quanta Module.
|
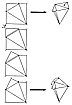 Fig. 986.515 |
986.515
 This construction method leaves a fourth right-triangular
corner piece
AC"B, which the dividers indicated-and subsequent trigonometry
confirmed__to be the
triangle exactly fitting the outer ABC-triangular-shaped
open end of the folded-together T
Quanta Module OABC. O" marks the fourth corner of the
square blank, and trigonometry
showed that C"A = C'B and C"B = AC, while AB of triangle
OBA by construction is
congruent with AB of triangle AC"B of the original layout.
So it is proven that the vector-
edged square COC'C" exactly equals the surface of the
T Quanta Module tetrahedron
CABO. (See Fig.
986.515.)
This construction method leaves a fourth right-triangular
corner piece
AC"B, which the dividers indicated-and subsequent trigonometry
confirmed__to be the
triangle exactly fitting the outer ABC-triangular-shaped
open end of the folded-together T
Quanta Module OABC. O" marks the fourth corner of the
square blank, and trigonometry
showed that C"A = C'B and C"B = AC, while AB of triangle
OBA by construction is
congruent with AB of triangle AC"B of the original layout.
So it is proven that the vector-
edged square COC'C" exactly equals the surface of the
T Quanta Module tetrahedron
CABO. (See Fig.
986.515.)
|

|
986.516
 The triangle AC"B is hinged to the T Quanta Module
along the mutual edge
AB, which is the hypotenuse of the small AC"B right
triangle. But as constructed the small
right triangle AC"B cannot be hinged (folded) to close
the T Quanta Module tetrahedron's
open-end triangular area ABC__despite the fact that the
hinged-on triangle AC"B and the
open triangle ABC are dimensionally identical. AC"B
is exactly the right shape and size
and area and can be used to exactly close the outer
face of the T Quanta Module
tetrahedron, if__but only if__it is cut off along line
BA and is then turned over so that its
faces are reversed and its B corner is now where its
A corner had been. This is to say that
if the square COC'C" is made of a cardboard sheet with
a red top side and a gray
underside, when we complete the tetrahedron folding
as previously described, cut off the
small corner triangle AC"B along line BA, reverse its
face and its acute ends, and then
address it to the small triangular ABC open end of the
tetrahedron CABO, it will fit exactly
into place, but with the completed tetrahedron having
three gray faces around vertex O
and one red outer face CAB. (See Fig.
986.508C.)
The triangle AC"B is hinged to the T Quanta Module
along the mutual edge
AB, which is the hypotenuse of the small AC"B right
triangle. But as constructed the small
right triangle AC"B cannot be hinged (folded) to close
the T Quanta Module tetrahedron's
open-end triangular area ABC__despite the fact that the
hinged-on triangle AC"B and the
open triangle ABC are dimensionally identical. AC"B
is exactly the right shape and size
and area and can be used to exactly close the outer
face of the T Quanta Module
tetrahedron, if__but only if__it is cut off along line
BA and is then turned over so that its
faces are reversed and its B corner is now where its
A corner had been. This is to say that
if the square COC'C" is made of a cardboard sheet with
a red top side and a gray
underside, when we complete the tetrahedron folding
as previously described, cut off the
small corner triangle AC"B along line BA, reverse its
face and its acute ends, and then
address it to the small triangular ABC open end of the
tetrahedron CABO, it will fit exactly
into place, but with the completed tetrahedron having
three gray faces around vertex O
and one red outer face CAB. (See Fig.
986.508C.)
|

|
986.517
 Following this closure procedure, when the AC"B triangles
of each of the
squares are cut off from COC'C" along line AB, and right
triangle AC"B is reversed in
face and its right-angle corner C" is made congruent
with the right-angle corner C of the T
Quanta Module's open-end triangle, then the B corner
of the small triangle goes into
congruence with the A corner of the open-end triangle,
and the A corner of the small
triangle goes into congruence with the B corner of the
open-end triangle__with the 90-
degree corner C becoming congruent with the small triangle's
right-angle corner C".
When all 120 of these T Quanta Module tetrahedra are
closed and assembled to produce
the triacontahedron, we will have all of the 360 gray
faces inside and all of the 120 red
faces outside, altogether producing an externally red
and an internally gray rhombic
triacontahedron.
Following this closure procedure, when the AC"B triangles
of each of the
squares are cut off from COC'C" along line AB, and right
triangle AC"B is reversed in
face and its right-angle corner C" is made congruent
with the right-angle corner C of the T
Quanta Module's open-end triangle, then the B corner
of the small triangle goes into
congruence with the A corner of the open-end triangle,
and the A corner of the small
triangle goes into congruence with the B corner of the
open-end triangle__with the 90-
degree corner C becoming congruent with the small triangle's
right-angle corner C".
When all 120 of these T Quanta Module tetrahedra are
closed and assembled to produce
the triacontahedron, we will have all of the 360 gray
faces inside and all of the 120 red
faces outside, altogether producing an externally red
and an internally gray rhombic
triacontahedron.
|

|
986.518
 In developing the paper-folding pattern with which
to construct any one of
these 120 identical T Quanta Module tetrahedra, we inadvertently
discovered it to be
foldable out of an exact square of construction paper,
the edge of which square is almost
(0.9995 of the prime vector 1) identical in length to
that of the prime vector radius of
synergetics' closest-packed unit-radius spheres, and
of the isotropic vector matrix, and
therefore of the radii and chords of the vector equilibrium__which
synergetics' vector (as
with all vectors) is the product of mass and velocity.
While the unit-vector length of our
everywhere-the-same energy condition conceptually idealizes
cosmic equilibrium, as prime
vector (Sec.
540.10)
it also inherently represents everywhere-the-same
maximum cosmic
velocity unfettered in vacuo__ergo, its linear velocity
(symbolized in physics as lower-case
c) is that of all radiation__whether beamed or piped
or linearly focused__the velocity of
whose unbeamed, omnidirectionally outward, surface growth
rate always amounts to the
second-powering of the linear speed. Ergo, omniradiance's
wave surface growth rate is c2.
In developing the paper-folding pattern with which
to construct any one of
these 120 identical T Quanta Module tetrahedra, we inadvertently
discovered it to be
foldable out of an exact square of construction paper,
the edge of which square is almost
(0.9995 of the prime vector 1) identical in length to
that of the prime vector radius of
synergetics' closest-packed unit-radius spheres, and
of the isotropic vector matrix, and
therefore of the radii and chords of the vector equilibrium__which
synergetics' vector (as
with all vectors) is the product of mass and velocity.
While the unit-vector length of our
everywhere-the-same energy condition conceptually idealizes
cosmic equilibrium, as prime
vector (Sec.
540.10)
it also inherently represents everywhere-the-same
maximum cosmic
velocity unfettered in vacuo__ergo, its linear velocity
(symbolized in physics as lower-case
c) is that of all radiation__whether beamed or piped
or linearly focused__the velocity of
whose unbeamed, omnidirectionally outward, surface growth
rate always amounts to the
second-powering of the linear speed. Ergo, omniradiance's
wave surface growth rate is c2.
|

|
986.519
 Since the edge length of the exactly 5.0000 (alpha) volumed
T Quanta Module
surface square is 0.9995 of the prime vector 1.0000
(alpha), the surface-field energy of the T
Quanta Module of minimum energy containment is 0.9995
V2 , where 1.0000 (alpha) V is the
prime vector of our isotropic vector matrix. The difference__0.0005__is
minimal but not
insignificant; for instance, the mass of the electron
happens also to be 0.0005 of the mass
of the proton.
Since the edge length of the exactly 5.0000 (alpha) volumed
T Quanta Module
surface square is 0.9995 of the prime vector 1.0000
(alpha), the surface-field energy of the T
Quanta Module of minimum energy containment is 0.9995
V2 , where 1.0000 (alpha) V is the
prime vector of our isotropic vector matrix. The difference__0.0005__is
minimal but not
insignificant; for instance, the mass of the electron
happens also to be 0.0005 of the mass
of the proton.
|
| Next Section: 986.520 |