900.00 MODELABILITY

900.01 Definition: Modelability

900.10 Modelability

900.11 Modelability is topologically conceptual in generalized principle independent of size and time: ergo, conceptual modelability is metaphysical.

900.12 Conceptual formulation is inherently empirical and as such is always special case sizing and always discloses all the physical characteristics of existence in time.

900.20 Synergetics

900.21 Synergetics is a book about models: humanly conceptual models; lucidly conceptual models; primitively simple models; rationally intertransforming models; and the primitively simple numbers uniquely and holistically identifying those models and their intertransformative, generalized and special case, number-value accountings.

900.30 Model vs Form

900.31 Model is generalization; form is special case.

900.32 The brain in its coordination of the sensing of each special case experience apprehends forms. Forms are special case. Models are generalizations of interrelationships. Models are inherently systemic. Forms are special case systems. Mind can conceptualize models. Brains can apprehend forms.

900.33 Forms have size. Models are sizeless, representing conceptuality independent of size.

901.00 Basic Disequilibrium LCD Triangle

901.01 Definition

901.02 The Basic Disequilibrium 120 LCD Spherical Triangle of synergetics is derived from the 15-great-circle, symmetric, three-way grid of the spherical icosahedron. It is the lowest common denominator of a sphere's surface, being precisely 1/120th of that surface as described by the icosahedron's 15 great circles. The trigonometric data for the Basic Disequilibrium LCD Triangle includes the data for the entire sphere and is the basis of all geodesic dome calculations. (See Sec.612.00.)

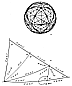Fig. 901.03 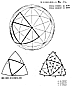Fig. 901.03

901.03 As seen in Sec. 610.20 there are only three basic structural systems in Universe: the tetrahedron, octahedron, and icosahedron. The largest number of equilateral triangles in a sphere is 20: the spherical icosahedron. Each of those 20 equiangular spherical triangles may be subdivided equally into six right triangles by the perpendicular bisectors of those equiangular triangles. The utmost number of geometrically similar subdivisions is 120 triangles, because further spherical-triangular subdivisions are no longer similar. The largest number of similar triangles in a sphere that spheric unity will accommodate is 120: 60 positive and 60 negative. Being spherical, they are positive and negative, having only common arc edges which, being curved, cannot hinge with one another; when their corresponding angle-and-edge patterns are vertex-mated, one bellies away from the other: concave or convex. When one is concave, the other is convex. (See Illus. 901.03 and drawings section.)

901.04 We cannot further subdivide the spherical icosahedron's equiangular triangles into similar, half-size, equiangular triangles, but we can in the planar icosahedron. When the sides of the triangle in the planar icosahedron are bisected, four similar half-size triangles result, and the process can be continued indefinitely. But in the spherical icosahedron, the smaller the triangle, the less the spherical excess; so the series of triangles will not be similar. Each corner of the icosahedron's equiangular triangles is 72 degrees; whereas the corners of its mid-edge-connecting triangle are each approximately 63 degrees.

901.10 Geodesic Dome Calculations

901.11 When two great-circle geodesic lines cross, they form two sets of similar angles, any one of which, paired with the other, will always add to 180º. (This we also learned in plane geometry.) When any one great circle enters into__or exits from__a spherical triangle, it will form the two sets of similar angles as it crosses the enclosing great-circle-edge-lines of that triangle.

901.12 As in billiards or in electromagnetics, when a ball or a photon caroms off a wall it bounces off at an angle similar to that at which it impinged.

901.13 If a great-circle-describing, inexhaustibly re-energized, satellite ball that was sufficiently resilient to remain corporeally integral, were suddenly to encounter a vertical, great-circle wall just newly mounted from its parent planet's sphere, it would bounce inwardly off that wall at the same angle that it would have traversed the same great-circle line had the wall not been there. And had two other great-circle walls forming a right spherical triangle with the first wall been erected just as the resilient ball satellite was hitting the first great-circle wall, then the satellite ball would be trapped inside the spherical-triangle-walled enclosure, and it would bounce angularly off the successively encountered walls in the similar-triangle manner unless it became aimed either at a corner vertex of the triangular wall trap, or exactly perpendicularly to the wall, in either of which cases it would be able to escape into the next spherical area Lying 180º ahead outside the first triangle's walls.

901.14 If, before the satellite bouncingly earned either a vertexial or perpendicular exit from the first-described spherical triangle (which happened to be dimensioned as one of the 120 LCD right triangles of the spherical icosahedron) great-circle walls representing the icosahedron's 15 complete great circles, were erect__thus constructing a uniform, spherical, wall patterning of 120 (60 positive, 60 negative) similar spherical, right triangles__we would find the satellite sphere bouncing around within one such spherical triangle at exactly the same interior or exiting angles as those at which it would have crossed, entered into, and exited, each of those great-circle boundaries of those 120 triangles had the wall not been so suddenly erected.

901.15 For this reason the great-circle interior mapping of the symmetrically superimposed other sets of 10 and 6 great circles, each of which__together with the 15 original great circles of the icosahedron__produces the 31 great circles of the spherical icosahedron's total number of symmetrical spinnabilities in respect to its 30 mid-edge, 20 mid-face, and 12 vertexial poles of half-as-many-each axes of spin. (See Sec. 457 .) These symmetrically superimposed, 10- and 6-great-circles subdivide each of the disequilibrious 120 LCD triangles into four lesser right spherical triangles. The exact trigonometric patterning of any other great circles orbiting the 120-LCD-triangled sphere may thus be exactly plotted within any one of these triangles.

901.16 It was for this reason, plus the discovery of the fact that the icosahedron__among all the three-and-only prime structural systems of Universe (see Sec. 610.20) __required the least energetic, vectorial, structural investment per volume of enclosed local Universe, that led to the development of the Basic Disequilibrium 120 LCD Spherical Triangle and its multifrequenced triangular subdivisioning as the basis for calculating all highfrequency, triangulated, spherical structures and structural subportions of spheres; for within only one disequilibrious LCD triangle were to be found all the spherical chord-factor constants for any desired radius of omnisubtriangulated spherical structure.

901.17 In the same way it was discovered that local, chord-compression struts could be islanded from one another, and could be only tensionally and non-inter-shearingly connected to produce stable and predictably efficient enclosures for any local energetic environment valving uses whatsoever by virtue of the approximately unlimited range of frequency-and-angle, subtriangle-structuring modulatability.

901.18 Because the 120 basic disequilibrious LCD triangles of the icosahedron have 2 l/2 times less spherical excess than do the 48 basic equilibrious LCD triangles of the vector equilibrium, and because all physical realizations are always disequilibrious, the Basic Disequilibrium 120 LCD Spherical Triangles become most realizably basic of all general systems' mathematical control matrixes.

901.19 Omnirational Control Matrix: Commensurability of Vector Equilibrium and Icosahedron The great-circle subdivisioning of the 48 basic equilibrious LCD triangles of the vector equilibrium may be representationally drawn within the 120 basic disequilibrious LCD triangles of the icosahedron, thus defining all the aberrations__and their magnitudes__existing between the equilibrious and disequilibrious states, and providing an omnirational control matrix for all topological, trigonometric, physical, and chemical accounting.

902.00 Properties of Basic Triangle

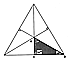Fig. 902.01

902.01 Subdivision of Equilateral Triangle: Both the spherical and planar equilateral triangles may be subdivided into six equal and congruent parts by describing perpendiculars from each vertex of the opposite face. This is demonstrated in Fig. 902.01, where one of the six equal triangles is labeled to correspond with the Basic Triangle in the planar condition.

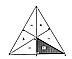Fig. 902.10

902.10 Positive and Negative Alternation: The six equal subdivision triangles of the planar equilateral triangle are hingeable on all of their adjacent lines and foldable into congruent overlays. Although they are all the same, their dispositions alternate in a positive and negative manner, either clockwise or counterclockwise.

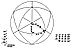Fig. 902.20

902.20 Spherical Right Triangles: The edges of all spherical triangles are arcs of great circles of a sphere, and those arc edges are measured in terms of their central angles (i.e., from the center of the sphere). But plane surface triangles have no inherent central angles, and their edges are measured in relative lengths of one of themselves or in special- case linear increments. Spherical triangles have three surface (corner) angles and three central (edge) angles. The basic data for the central angles provided below are accurate to 1/1,000 of a second of arc. On Earth 1 nautical mile = 1 minute of arc 1 nautical mile = approximately 6,000 feet 1 second of arc = approximately 100 feet 1/l,000 second of arc = approximately 1/10 foot 1/1,000 second of arc = approximately 1 inch These calculations are therefore accurate to one inch of Earth's arc.

902.21 The arc edges of the Basic Disequilibrium 120 LCD Triangle as measured by their central angles add up to 90° as do also three internal surface angles of the triangle's ACB corner: BCE = 20° 54' 18.57" = ECF ECD = 37° 22' 38.53" = DCE DCA = 31° 43' 02.9" --------------- = ACD 90° 00' 00"

902.22 The spherical surface angle BCE is exactly equal to two of the arc edges of the Basic Disequilibrium 120 LCD Triangle measured by their central angle. BCE = arc AC = arc CF = 20° 54' 18.57".

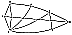Fig. 902.30

902.30 Surface Angles and Central Angles: The Basic Triangle ACB can be folded on the lines CD and CE and EF. We may then bring AC to coincide with CF and fold BEF down to close the tetrahedron, with B congruent with D because the arc DE = arc EB and arc BF = arc AD. Then the tetrahedron's corner C will fit exactly down into the central angles AOC, COB, and AOB. (See Illus. 901.03 and 902.30.)

902.31 As you go from one sphere-foldable great-circle set to another in the hierarchy of spinnable symmetries (the 3-, 4-, 6-, 12-sets of the vector equilibrium's 25- great-circle group and the 6-, 10-, 15-sets of the icosahedron's 31-great-circle group), the central angles of one often become the surface angles of the next-higher-numbered, more complex, great-circle set while simultaneously some (but not all) of the surface angles become the respective next sphere's central angles. A triangle on the surface of the icosahedron folds itself up, becomes a tetrahedron, and plunges deeply down into the congruent central angles' void of the icosahedron (see Sec. 905.47 ).

902.32 There is only one noncongruence- the last would-be hinge, EF is an external arc and cannot fold as a straight line; and the spherical surface angle EBF is 36 degrees whereas a planar 30 degrees is called for if the surface is cast off or the arc subsides chordally to fit the 90-60-30 right plane triangle.

902.33 The 6 degrees of spherical excess is a beautiful whole, rational number excess. The 90-degree and 60-degree corners seem to force all the excess into one corner, which is not the way spherical triangles subside. All the angles lose excess in proportion to their interfunctional values. This particular condition means that the 90 degrees would shrink and the 60 degrees would shrink. I converted all the three corners into seconds and began a proportional decrease study, and it was there that I began to encounter a ratio that seemed rational and had the number 31 in one corner. This seemed valid as all the conditions were adding up to 180 degrees or 90 degrees as rational wholes even in both spherical and planar conditions despite certain complementary transformations. This led to the intuitive identification of the Basic Disequilibrium 120 LCD Triangle's foldability (and its fall-in-ability into its own tetra-void) with the A Quanta Module, as discussed in Sec. 910 which follows.