986.310 Strategic Use of Min-max Cosmic System Limits
986.311 The maximum limit set of identical facets into which any system can be divided consists of 120 similar spherical right triangles ACB whose three corners are 60 degrees at A, 90 degrees at C, and 36 degrees at B. Sixty of these right spherical triangles are positive (active), and 60 are negative (passive). (See Sec. 901.)
986.312 These 120 right spherical surface triangles are described by three different central angles of 37.37736814 degrees for arc AB, 31.71747441 degrees for arc BC, and 20.90515745 degrees for arc AC__which three central-angle arcs total exactly 90 degrees. These 120 spherical right triangles are self-patterned into producing 30 identical spherical diamond groups bounded by the same central angles and having corresponding flat-faceted diamond groups consisting of four of the 120 angularly identical (60 positive, 60 negative) triangles. Their three surface corners are 90 degrees at C, 31.71747441 degrees at B, and 58.2825256 degrees at A. (See Fig. 986.502.)
986.313 These diamonds, like all diamonds, are rhombic forms. The 30-symmetrical- diamond system is called the rhombic triacontahedron: its 30 mid-diamond faces (right- angle cross points) are approximately tangent to the unit-vector-radius sphere when the volume of the rhombic triacontahedron is exactly tetravolume-5. (See Fig. 986.314.)

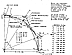Fig. 986.314 		986.314 I therefore asked Robert Grip and Chris Kitrick to prepare a graphic comparison of the various radii and their respective polyhedral profiles of all the symmetric polyhedra of tetravolume 5 (or close to 5) existing within the primitive cosmic hierarchy (Sec. 982.62) __i.e. other than those of tetravolumes 1, 2, 3, 4, and 6__which carefully drafted drawing of the tetravolume-5 polyhedra (and those polyhedra "approximately" tetravolume S) my colleagues did prepare (see Fig. 986.314). These exactly tetravolume-5 polyhedra are, for example__
  1. the icosahedron with outer edges of unit vector length;
  2. the icosahedron of outer vertex radius of unit vector length;
  3. the regular dodecahedron of unit vector edge; and
  4. the regular dodecahedron of unit vector radius
__all of which show that they have only a slightly greater radius length than that of the prime vector.
986.315 The chart of the polyhedral profiles (Fig. 986.314) shows the triacontahedron of tetravolume 5 having its mid-diamond-face point C at a distance outward radially from the volumetric center that approximately equals the relative length of the prime vector. I say "approximately" because the trigonometrically calculated value is .999483332 instead of 1, a 0.0005166676 radial difference, which__though possibly caused in some very meager degree by the lack of absolute resolvability of trigonometric calculations themselves__is on careful mathematical review so close to correct as to be unalterable by any known conventional trigonometric error allowance. It is also so correct as to hold historical significance, as we shall soon discover. Such a discrepancy is so meager in relation, for instance, to planet Earth's spheric diameter of approximately 8,000 miles that the spherical surface aberration would be approximately the same as that existing between sea level and the height of Mount Fuji, which is only half the altitude of Mount Everest. And even Mount Everest is invisible on the Earth's profile when the Earth is photographed from outer space. The mathematical detection of such meager relative proportioning differences has time and again proven to be of inestimable value to science in first detecting and then discovering cosmically profound phenomena. In such a context my "spherical energy content" of 4.99, instead of exactly 5, became a thought-provoking difference to be importantly remembered.
986.316 By careful study of the Grip-Kitrick drawings of tetravolume-5 polyhedra it is discovered that the graphically displayed zones of radial proximity to one another of all the tetravolume-5 symmetric polyhedra (Fig. 986.314) describe such meager radial differences at their respective systems' outermost points as to suggest that their circumferential zone enclosed between the most extremely varied and the most inwardly radiused of all their axially spun vertexes of the exact tetravolume-5 polyhedra may altogether be assumed to constitute the zone of limit cases of radiantly swept-out and pulsating tetravolume-5 kinetic systems.
986.317 Recognizing that polyhedra are closed systems and that there are only seven cases of symmetrical subdivisioning of systems by the most economical great-circle spinnings (and most economically by the chords of the great-circle arcs), we discover and prove structurally that the maximum-limit abundance of a unit-symmetrical-polyhedral- system's identical facetings is the rhombic triacontahedron, each of whose 30 symmetrical diamond planar faces may be symmetrically subdivided into four identical right triangles (30 × 4=120), and we find that the triacontahedron's 120-spherical-right-triangled frame of system reference is the maximum-limit case of identical faceting of any and all symmetrical polyhedral systems in Universe. This maximum-limit-system structuring proof is accomplished by the physically permitted, great-circle-spun, hemispherical self-halvings, as permitted by any and all of the seven cosmic limit cases of symmetric systems' being spun-defined around all the respective system's geometrically definitive (ergo, inherent) axes of symmetrical spinnability. It is thus that we learn experimentally how all the symmetric systems of Universe self-fractionate their initial system unities into the maximum number of omniangularly identical surface triangles outwardly defining their respective internal-structure tetrahedra whose angles-central or surface-are always independent of a system's time-size considerations. And because they are independent of time-size considerations, such minimum-maximum limit-case ranges embrace all the symmetrical polyhedral systems' generalized-primitive-conceptuality phenomena.
986.400 T Quanta Module
986.401 Consideration 12: Dynamic Spinning of Rhombic Triacontahedron
986.402 I then speculated that the only-by-spinning-produced, only superficially apparent "sphericity" could be roundly aspected by spinning the rhombic triacontahedron of tetravolume 5. This rational volumetric value of exactly 5 tetravolumes placed the rhombic triacontahedron neatly into membership in the primitive hierarchy family of symmetric polyhedra, filling the only remaining vacancy in the holistic rational-number hierarchy of primitive polyhedral volumes from 1 through 6, as presented in Table 1053.51A.
986.403 In the isotropic vector matrix system, where R = radius and PV = prime vector, PV = 1 = R__ergo, PVR = prime vector radius, which is always the unity of VE. In the 30-diamond-faceted triacontahedron of tetravolume 5 and the 12-diamond-faceted dodecahedron of tetravolume 6, the radius distances from their respective symmetric polyhedra's volumetric centers O to their respective mid-diamond faces C (i.e., their short- and-long-diamond-axes' crossing points) are in the rhombic triacontahedral case almost exactly PVR__i.e., 0.9994833324 PVR__and in the rhombic dodecahedral case exactly PVR, 1.0000 (alpha) PVR.
986.404 In the case of the rhombic dodecahedron the mid-diamond-face point C is exactly PVR distance from the polyhedral system's volumetric (nucleic) center, while in the case of the rhombic triacontahedron the point C is at approximately PVR distance from the system's volumetric (nucleic) center. The distance outward to C from the nucleic center of the rhombic dodecahedron is that same PVR length as the prime unit vector of the isotropic vector matrix. This aspect of the rhombic triacontahedron is shown at Fig. 986.314.

Fig. 986.405 		986.405 The symmetric polyhedral centers of both the rhombic dodecahedron and the rhombic triacontahedron may be identified as 0, and both of their respective external diamond faces' short axes may be identified as A-A and their respective long axes as B-B. Both the rhombic dodecahedron's and the triacontahedron's external diamond faces ABAB and their respective volumetric centers O describe semiasymmetric pentahedra conventionally labeled as OABAB. The diamond surface faces ABA of both OABAB pentahedra are external to their respective rhombic-hedra symmetrical systems, while their triangular sides OAB (four each) are internal to their respective rhombichedra systems. The angles describing the short A-A axis and the long B-B axis, as well as the surface and central angles of the rhombic dodecahedron's OABAB pentahedron, all differ from those of the triacontahedron's OABAB pentahedron.
Next Section: 986.410
Copyright © 1997 Estate of R. Buckminster Fuller