Primary and Secondary Great-circle Symmetries
|
|
987.130
Primary and Secondary Great-circle Symmetries
|
|
|
987.131
There are seven other secondary symmetries based on
the pairing into spin
poles of vertexes produced by the complex secondary
crossings of one another of the
seven original great circle symmetries.
|
 Fig. 987.132E 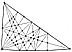 Fig. 987.132F |
987.132
The primary and secondary icosa symmetries altogether
comprise 121 = 112
great circles. (See Fig.
987.132E.)
|
|
|
987.133
The crossing of the primary 12 great circles of the
VE at G (see Fig.
453.01,
as revised in third printing) results in 12 new axes
to generate 12 new great circles. (See color plate 12.)
|
|
|
987.134
The crossing of the primary 12 great circles of the
VE and the four great
circles of the VE at C (Fig.
453.01) results in 24 new
axes to generate 24 new great
circles. (See color plate 13.)
|
|
|
987.135
The crossing of the primary 12 great circles of the
VE and the six great
circles of the VE at E (Fig.
453.01) results in 12 new
axes to generate 12 new great
circles. (See color plate 14.)
|
|
|
987.136
The remaining crossing of the primary 12 great circles
of the VE at F (Fig.
453.01
results in 24 more axes to generate 24 new great
circles. (See color plate 15.)
|
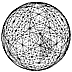 Fig. 987.137B 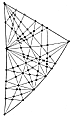 Fig. 987.137C |
987.137
The total of the above-mentioned secondary great circles
of the VE is 96
new great circles (See Fig
987.137B.)
|
|
|
987.200
Cleavagings Generate Polyhedral Resultants
|
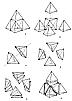 Fig. 987.210 |
987.210
Symmetry #1 and Cleavage #1
|
|
|
987.211
In Symmetry #l and Cleavage #1 three great circles-the
lines in Figs.
987.210
A through F__are successively and cleavingly spun by
using the midpoints of
each of the tetrahedron's six edges as the six poles
of three intersymmetrical axes of
spinning to fractionate the primitive tetrahedron, first
into the 12 equi-vector-edged octa,
eight Eighth-octa (each of l/2-tetravolume), and four
regular tetra (each of l-tetravolume).
|
|
|
987.212
A simple example of Symmetry #1 appears at Fig.
835.11.
Cleavage #1 is
illustrated at Fig.
987.210E.
|
|
|
987.213 Figs. 987.210A-E demonstrate Cleavage #1 in the following sequences: (1) The red great circling cleaves the tetrahedron into two asymmetric but identically formed and identically volumed "chef's hat" halves of the initial primitive tetrahedron (Fig. 987.210). (2) The blue great circling cleavage of each of the two "chef's hat" halves divides them into four identically formed and identically volumed "iceberg" asymmetrical quarterings of the initial primitive tetrahedron (Fig. 987.210B). (3) The yellow great circling cleavage of the four "icebergs" into two conformal types of equivolumed one- Eighthings of the initial primitive tetrahedron__four of these one-Eighthings being regular tetra of half the vector-edge-length of the original tetra and four of these one-Eighthings being asymmetrical tetrahedra quarter octa with five of their six edges having a length of the unit vector = 1 and the sixth edge having a length of sqrt(2) = 1.414214. (Fig. 987.210C.) |
|
|
987.220
Symmetry #2 and Cleavage #4:
|
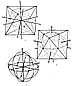 Fig. 987.221 |
987.221
In Symmetry #2 and Cleavage #4 the four-great-circle
cleavage of the
octahedron is accomplished through spinning the four
axes between the octahedron's eight
midface polar points, which were produced by Cleavage
#2. This symmetrical four-great-
circle spinning introduces the nucleated 12 unit-radius
spheres closest packed around one
unit-radius sphere with the 24 equi-vector outer-edge-chorded
and the 24 equi-vector-
lengthed, congruently paired radii__a system called the
vector equilibrium. The VE has 12
external vertexes around one center-of-volume vertex,
and altogether they locate the
centers of volume of the 12 unit-radius spheres closest
packed around one central or one
nuclear event's locus-identifying, omnidirectionally
tangent, unit-radius nuclear sphere.
|
|
|
987.222
The vectorial and gravitational proclivities of nuclear
convergence of all
synergetics' system interrelationships intercoordinatingly
and intertransformingly permit
and realistically account all radiant entropic growth
of systems as well as all gravitational
coherence, symmetrical contraction, and shrinkage of
systems. Entropic radiation and
dissipation growth and syntropic gravitational-integrity
convergency uniquely differentiate
synergetics' natural coordinates from the XYZ-centimeter-gram-second
abstract
coordinates of conventional formalized science with
its omniinterperpendicular and
omniinterparallel nucleus-void frame of coordinate event
referencing.
|
|
|
987.223
Symmetry #2 is illustrated at Fig.
841.15A.
|
| Next Section: 987.230 |