Superficial and Volumetric Hierarchies
|
|
1053.00
Superficial and Volumetric Hierarchies
|
|
|
1053.10
Spherical Triangular Grid Tiles: The interrelationship
of the vector
equilibrium and the icosahedron when their respective
25- and 31-great-circle grids are
superimposed on one another, with the center of area
of the vector equilibrium's eight
spherical triangles congruent with the areal centers
of eight of the icosahedron's 20
spherical triangles, reveals a fundamental, asymmetrical,
six-axis, alternative, impulsive-
pulsative potential of surface intertransformabilities
in respect to which the vector
equilibrium serves as the zero between the positive
and negative, "relative" asymmetry,
deviations.
|
|
|
1053.11
The vector equilibrium's 25 and the icosahedron's 31
spherical-great-circle
grids manifest different least-common-denominator, identically
angled, spherical triangular
"tiles," which together exactly cover and subdivide
the spherical surface in whole even
numbers of tiles; the vector equilibrium having 48 such
LCD triangles and the icosahedron
having 2 1/2 times as many LCD triangles, i.e., 120.
|
|
|
1053.12
The fundamental fiveness of the icosahedron is split
two ways, with 2 1/2
going one way (the outside-out way) and 2 1/2 going
the other way (the inside-out way).
The least-common-denominator triangular surface subdivision
of the vector equilibrium's
sphere provides 48 angularly identical (24 inside-out
and 24 outside-out) subdivisions as
spherical surface "tiles" that exactly cover one sphere.
|
|
|
1053.13
120/48 = 2 1/2; and there are always both the four
positively skew-rotated
and the four negatively skew-rotated sets of spherical
triangles (two sets of four each),
symmetrically borrowed from among the spherical total
of 20 equiangled, spherical
triangles of each of two spherical icosahedra (each
of radius 1)_which four out of 20
(20/4 = 5) spherical icosahedron's triangles' centers
of area are exactly concentrically
registerable upon every other one of the spherical octahedron's
eight triangles, which areal
centers of the octahedron's eight triangles are also
always concentrically and
symmetrically in register with the eight equiangled,
spherical triangles of the spherical
vector equilibrium when the octahedron and the vector
equilibrium spheres are all of the
same unity-l radius. With this registration of four
out of eight centers of the icosahedron
upon the octahedron-vector equilibrium's eight triangular
surfaces each, we find that one
icosa set of four skews rotationally positive, while
the set of four from another
icosahedron phase registers the negative skew rotation,
which is a +30 degrees or -30
degrees circumferentially-away-from-zero, rotational
askewness for a total of 60 degrees
differential between the extremes of both. The remaining
16 out of the total of 20 triangles
of each of the two different (plus-or-minus-30-degree)
phase icosahedra, subdivide
themselves in four sets of four each, each of which
sets of four arrange themselves in
polarized symmetry upon each of the octahedron's four
other spherical triangles which are
not concentrically occupied by either the positively-
or negatively-skew, concentric sets, of
four each, triangles, neither of which four sets of
four each non-triangularly-concentric
sets repeat the other sets' complementary, asymmetric
but polarized, array in
superimposition upon the octahedron's four nonconcentrically
occupied triangles.
|
|
|
1053.14
It was in discovering this alternate, concentric askewness
of icosa-upon-
octa, however, that we also learned that the symmetrical,
equiangular, spherical triangle
areas, filled evenly__but rotationally askew__with sets
of 15 of the icosahedron's 120
LCD triangles, exactly registered with the spherical
surface area of one of the spherical
octahedron's eight triangular faces (each of which are
bound by 90-degree corners and 90-
degree arc edges). This meant, however, that the 15
LCD icosa triangles' plusly-rotated
askew phases are not congruent with one another but
are superimposed in alternately
askewed arrays, both in the cases of the four concentric
triangles and in the cases of the
nonconcentrically-registered triangles.
|
|
|
1053.15
Because each of the octahedron's eight faces is subdivided
by its respective
six sets of spherical "right" triangles (three positive__three
negative), whose total of 6 × 8
= 48 triangles are the 48 LCD's vector-equilibrium,
symmetric-phase triangles, and
because 120/48 = 2 1/2, it means that each of the vector
equilibrium's 48 triangles has
superimposed upon it 2 1/2 positively askew and 2 1/2
negatively askew triangles from out
of the total inventory of 120 LCD asymmetric triangles
of each of the two sets,
respectively, of the two alternate phases of the icosahedron's
limit of rotational aberrating
of the vector equilibrium. This 2 1/2 positive superimposed
upon the 2 1/2 negative, 120-
LCD picture is somewhat like a Picasso duo-face painting
with half a front view
superimposed upon half a side view. It is then in transforming
from a positive two-and-
one-halfness to a negative two-and-one-halfness that
the intertransformable vector-
equilibrium-to-icosahedron, icosahedron-to-vector-equilibrium,
equilibrious-to-
disequilibriousness attains sumtotally and only dynamically
a spherical fiveness (see Illus.
982.61 in color section).
|
|
|
1053.16
This half-in-the-physical, half-in-the-metaphysical;
i.e., half-conceptual, half-
nonconceptual; i.e., now you see it, now you don't__and
repeat, behavior is characteristic
of synergetics with its nuclear sphere being both concave
and convex simultaneously,
which elucidates the microcosmic, turn-around limit
of Universe as does the c2 the
spherical-wave-terminal-limit velocity of outwardness
elucidate the turn-around-and-
return limit of the macrocosm.
|
|
|
1053.17
This containment of somethingness by uncontained nothingness:
this split
personality +2 1/2, -2 l/2; + 5, - 5, + 0, -0; plural
unity: this multiplicative twoness and
additive twoness of unity; this circumferential-radial;
this birth-death, birth-death; physical-
metaphysical, physical-metaphysical; yes-no, yes-no-ness;
oscillating-pulsating geometrical
intertransformability field; Boltzmann importing-exporting
elucidates the a priori nature of
the associative-disassociative; entropic-syntropic;
energetic-synergetic inherency of cosmic
discontinuity with its ever locally renewable cyclic
continuities, wherewith Universe
guarantees the eternally regenerative scenario integrity.
|
|
|
1053.20
Platonic Polyhedra: There are 48 spherical triangular
tiles of the vector
equilibrium nuclear sphere, which 48 triangles' pattern
can be symmetrically subdivided
into five different sets of symmetrical interpatterning
which coincide exactly with the
projection outward onto a sphere of the five omnisymmetrical
planar-defined Platonic
polyhedra, whose linear edges are outlined by the respective
chords of the congruent
vector equilibrium's symmetrical 25-great-circle grid
and the icosahedron's 31-great-circle
grid. These equiedged Platonic solids are the icosahedron,
the octahedron, the cube, the
tetrahedron, and the regular dodecahedron. (The vector
equilibrium is one of the
Archimedean polyhedra; it was called cuboctahedron by
the Greeks.)
|
|
|
1053.21
The chords of these five spherical geometric integrities
all interact to
produce those well-known equiedged polyhedra commonly
associated with Plato. The
intervolumetric quantation of these five polyhedra is
demonstrated as rational when
referenced to the tetrahedron as unity. Their surface
values can also be rationally
quantized in reverse order of magnitude by the 48 spherical
triangle tiles in whole, low-
order, even numbers. These hierarchies are a discovery
of synergetic geometry.
|
|
|
1053.30
LCD Superficial Quantation of Systems: Because the
icosahedron's 31-
great-circle grid discloses 120 least-common-denominator,
spherical triangular, whole
tiling units, we require a special-case, least-common-surface-denominator
identity as a
name for the 48 spherical tiles of the vector equilibrium.
The 120 spherical surface
triangular tiles (60 insideout and 60 outside-out) do
indeed constitute the least-common-
spherical and planar polyhedra's whole-surface denominators,
ergo LCDs, of all closed
systems; for all systems are either simplex (atomic)
or complex (molecular) manifests of
polyhedra. All systems, symmetrical or asymmetrical,
have fundamental insideness (micro)
and outsideness (macro) irrelevancies that leave the
residual-system relevancies
accountable as topological characteristics of the polyhedra.
|
|
|
1053.31
As we have learned elsewhere, the sphere, as demonstrated
by the spherical
icosahedral subdivisions, discloses a different least-common-denominator
spherical
subdivision in which there are 120 such tiles (60 positive
and 60 negative), which are
generalizable mathematically as the least-common surface
denominator of surface unity,
ergo, of systems in general superficially quantated.
Because the icosahedron provides the
maximum asymmetries into which the vector equilibrium's
universally zero-balanced
surface can be transformed, and since the effect of
the icosahedron__which introduces the
prime number five into Universe systems__is one of transforming,
or splitting, equilibrium
two ways, we find time after time that the interrelationship
of the vector equilibrium and
the icosahedron surfaces to be one such elegant manifestation
of the number 2 l/2__2 1/2
positive and 2 1/2 negative, of which the icosahedron's
fiveness consists. This half-
positive and half-negative dichotomization of systems
is the counterpart in pure principle
of the nuclear accounting that finds that the innermost
ball of the closest-packed
symmetrical aggregate always belongs half to a positive
world and half to a negative
world; that is, the inbound half (implosive) and the
outbound half (explosive) altogether
make a kinetically regenerative whole centrality that
never belongs completely to either
world.
|
|
|
1053.32
It is a condition analogous to the sphere with its
always and only
complementarity of insideness and outsideness, convexity
and concavity. A sphere may be
thought of as half concave and half convex as well as
having two different poles.
|
|
|
1053.33
For the moment, considering particularly spherical-system
surfaces, we find
the same 2 l/2-ness relationship existing between the
vector equilibrium and the
icosahedron, with their respective least common denominator's
surface triangle building
tiles (of which the vector equilibrium's 48 LCDs have
five of the equiedged Platonic solids
and the icosahedron's 120 LCDs have two of the equiedged
Platonic solids). The
icosahedron-coexistent pentagonal dodecahedron is the
special-case system of domains of
the icosahedron's 12 vertexes; it is not a structure
in its own right. Plato's five
omniequifaceted, equiedged and -vertexed, "solids" were
the cube, tetrahedron,
octahedron, icosahedron, and dodecahedron. All five
of these solids are rationally
accounted by the LCD spherical surface triangular tilings
of the vector equilibrium and the
icosahedron.
|
|
|
1053.34
The icosahedron has 120 triangles (60+, 60-), which
are the least common
denominators of spherical surface unity of Universe;
ergo, so important as to have
generated, for instance, the ancient Babylonians' adoption
of 60 both for increments of
time and for circular mensuration. The Babylonians attempted
to establish a
comprehensive coordinate mensural system that integrated
time and matter. Their artifacts
show that they had discovered the 60 positive and 60
negative, 120 spherical right
triangles of spheres. That their sixtyness did not uncover
nature's own rational coordinate
system should not be permitted to obscure the fact that
the Babylonians were initiating
their thinking systematically in polyhedral spherical
wholeness and in 60-degree vs. 90-
degree coordination, which was not characteristic of
the geometrical exploration of a later
date by the Egyptians and Greeks, who started very locally
with lines, perpendiculars, and
planes.
|
|
|
1053.35
The great 2 l/2 transformation relations between the
vector equilibrium and
the icosahedron once again manifest in surface equanimity
as the LCD surface triangular
tiling, which is 2 1/2 times 48, or 120.
|
|
|
1053.36
Sphere: Volume-surface Ratios: The largest number of
similar triangles
into which the whole surface of a sphere may be divided
is 120. (See Secs.
905
and
986.)
The surface triangles of each of these 120 triangles
consist of one angle of 90 degrees, one
of 60 degrees, and one of 36 degrees. Each of these
120 surface triangles is the fourth face
of a similar tetrahedron whose three other faces are
internal to the sphere. Each of these
tetra has the same volume as have the A or B Quanta
Modules. Where the tetra is 1,
the volume of the rhombic triacontahedron is approximately
5. Dividing 120 by 5 = 24 =
quanta modules per tetra. The division of the rhombic
triacontahedron of approximately
tetravolume-5 by its 120 quanta modules discloses another
unit system behavior of the
number 24 as well as its appearance in the 24 external
vector edges of the VE. (See Sec.
1224.21)
|
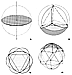 Fig. 1053.37 |
1053.37
Since the surface of a sphere exactly equals the internal
area of the four great
circles of the sphere, and since the surface areas of
each of the four triangles of the
spherical tetrahedron also equal exactly one-quarter
of the sphere's surface, we find that
the surface area of one surface triangle of the spherical
tetrahedron exactly equals the
internal area of one great circle of the sphere; wherefore
|
|
|
1053.40
Superficial Hierarchy: We have here a total spherical
surface
subdivisioning hierarchy predicated upon (a) the relative
number of LCD (48/n) tiles
necessary to define each of the following's surface
triangles, wherein the tetrahedron
requires 12; the octahedron 6; cube 8; and rhombic dodecahedron
4; in contradistinction
to (b) their respective volumetric quantations expressed
in the terms of the planar-faceted
tetrahedron as unity.
|
|
|
1053.41
Table: Spherical Surface Hierarchy
|
|
|
1053.50
Volumetric Hierarchy: With a nuclear sphere of radius-1,
the volumetric
hierarchy relationship is in reverse magnitude of the
superficial hierarchy. In the surface
hierarchy, the order of size reverses the volumetric
hierarchy, with the tetrahedron being
the largest and the rhombic dodecahedron the smallest.
|
|
|
1053.51
Table: Volumetric Hierarchy: The space quantum equals
the space domain
of each closest-packed nuclear sphere:
(Footnote 10: The octahedron is always double, ergo, its fourness of volume is its prime number manifest of two, which synergetics finds to be unique to the octahedron.) |
|
|
1053.51A
Table: Volumetric Hierarchy (revised): The space quantum
equals the
space domain of each closest-packed nuclear sphere:
|
|
|
1053.60
Reverse Magnitude of Surface vs. Volume: Returning
to our
consideration of the reverse magnitude hierarchy of
the surface vs. volume, we find that
both embrace the same hierarchical sequence and have
the same membership list, with the
icosahedron and vector equilibrium on one end of the
scale and the tetrahedron on the
other. The tetrahedron is the smallest omnisymmetrical
structural system in Universe. It is
structured with three triangles around each vertex;
the octahedron has four, and the
icosahedron has five triangles around each vertex. We
find the octahedron in between,
doubling its prime number twoness into volumetric fourness,
as is manifest in the great-
circle foldability of the octahedron, which always requires
two sets of great circles,
whereas all the other icosahedron and vector equilibrium
31 and 25 great circles are
foldable from single sets of great circles .
|
|
|
1053.601
Octahedron: The octahedron__both
numerically and geometrically__should
always be considered as quadrivalent; i.e., congruent
with self; i.e., doubly present. In the
volumetric hierarchy of prime-number identities we identify
the octahedron's prime-
number twoness and the inherent volume-fourness (in
tetra terms) as volume 22, which
produces the experiential volume 4.
|
|
|
1053.61
The reverse magnitudes of the surface vs. volume hierarchy
are completely
logical in the case of the total surface subdivision
starting with system totality. On the
other hand, we begin the volumetric quantation hierarchy
with the tetrahedron as the
volumetric quantum (unit), and in so doing we build
from the most common to the least
common omnisymmetrical systems of Universe. In this
system of biggest systems built of
smaller systems, the tetrahedron is the smallest, ergo,
most universal. Speaking
holistically, the tetrahedron is predominant; all of
this is analogous to the smallest chemical
element, hydrogen, being the most universally present
and plentiful, constituting the
preponderance of the relative abundance of chemical
elements in Universe.
|
|
|
1053.62
The tetrahedron can be considered as a whole system
or as a constituent of
systems in particular. It is the particulate.
|
|
|
1053.70
Container Structuring: Volume-surface Ratios
|
|
|
1053.71
When attempting to establish an international metric
standard of measure for
an integrated volume-weight unit to be known as "one
gram" and deemed to consist of
one cubic centimeter of water, the scientists overlooked
the necessity for establishing a
constant condition of temperature for the water. Because
of expansion and contraction
under changing conditions of temperature a constant
condition of 4 degrees centigrade
was later established internationally. In much the same
way scientists have overlooked and
as yet have made no allowance for the inherent variables
in entropic and syntropic rates of
energy loss or gain unique to various structurally symmetrical
shapes and sizes and
environmental relationships. (See Sec.
223.80, "Energy
Has Shape.") Not only do we have
the hierarchy of relative volume containments respectively
of equiedged tetra, cube, octa,
icosa, "sphere," but we have also the relative surface-to-volume
ratios of those geometries
and the progressive variance in their relative structural-strength-to-surface
ratios as
performed by flat planes vs simple curvature; and as
again augmented in strength out of
the same amount of the same material when structured
in compound curvature.
|
|
|
1053.72
In addition to all the foregoing structural-capability
differentials we have the
tensegrity variables
(see Chap. 7),
as all these relate
to various structural capabilities of
various energy patternings as containers to sustain
their containment of the variously
patterning contained energies occurring, for instance,
as vacuum vs crystalline vs liquid vs
gaseous vs plasmic vs electromagnetic phases; as well
as the many cases of contained
explosive and implosive forces. Other structural variables
occur in respect to different
container-contained relationships, such as those of
concentrated vs distributive loadings
under varying conditions of heat, vibration, or pressure;
as well as in respect to the
variable tensile and compressive and sheer strengths
of various chemical substances used
in the container structuring, and their respective heat
treatments; and their sustainable
strength-time limits in respect to the progressive relaxing
or annealing behaviors of various
alloys and their microconstituents of geometrically
variant chemical, crystalline, structural,
and interproximity characteristics. There are also external
effects of the relative size-
strength ratio variables that bring about internal interattractiveness
values in the various
alloys as governed by the second-power rate, i.e., frequency
of recurrence and intimacy of
those alloyed substances' atoms.
|
|
|
1053.73
As geometrical systems are symmetrically doubled in
linear dimension, their
surfaces increase at a rate of the second power while
their volumes increase at a third-
power rate. Conversely, as we symmetrically halve the
linear dimensions of geometrical
systems, their surfaces are reduced at a second-root
rate, while their volumes decrease at a
third-root rate.
|
|
|
1053.74
A cigar-shaped piece of steel six feet (72 inches)
long, having a small hole
through one end and with a midgirth diameter of six
inches, has an engineering slenderness
ratio (length divided by diameter) of 12 to 1: It will
sink when placed on the surface of a
body of water that is more than six inches deep. The
same-shaped, end-pierced piece of
the same steel of the same 12-to-1 slenderness ratio,
when reduced symmetrically in length
to three inches, becomes a sewing needle, and it will
float when placed on the surface of
the same body of water. Diminution of the size brought
about so relatively mild a
reduction in the amount of surface of the steel cigar-needle's
shape in respect to the great
change in volume__ergo, of weight__that its shape became
so predominantly "surface"
and its relative weight so negligible that only the
needle's surface and the atomic-intimacy-
produced surface tension of the water were importantly
responsible for its
interenvironmental relationship behaviors.
|
|
|
1053.75
For the same reasons, grasshoppers' legs in relation
to a human being's legs
have so favorable a volume-to-surface-tension relationship
that the grasshopper can jump
to a height of 100 times its own standing height (length)
without hurting its delicate legs
when landing, while a human can jump and fall from a
height of only approximately three
times his height (length) without breaking his legs.
|
|
|
1053.76
This same volume-to-surface differential in rate of
change with size increase
means that every time we double the size of a container,
the contained volume increases
by eight while the surface increases only fourfold.
Therefore, as compared to its previous
half-size state, each interior molecule of the atmosphere
of the building whose size has
been symmetrically doubled has only half as much building
surface through which that
interior molecule of atmosphere can gain or lose heat
from or to the environmental
conditions occurring outside the building as conductively
transferable inwardly or
outwardly through the building's skin. For this reason
icebergs melt very slowly but
accelerate progressively in the rate of melting. For
the same reason a very different set of
variables governs the rates of gain or loss of a system's
energy as the system's size
relationships are altered in respect to the environments
within which they occur.
|
|
|
1053.77
As oil tankers are doubled in size, their payloads
grow eightfold in quantity
and monetary value, while their containing hulls grow
only fourfold in quantity and cost.
Because the surface of the tankers increases only fourfold
when their lengths are doubled
and their cargo volume increases eightfold, and because
the power required to drive them
through the sea is proportional to the ship's surface,
each time the size of the tankers is
doubled, the cost of delivery per cargo ton, barrel,
or gallon is halved. The last decade has
seen a tenfolding in the size of the transoceanic tankers
in which both the cost of the ship
and the transoceanic delivery costs have become so negligible
that some of the first such
shipowners could almost afford to give their ships away
at the end of one voyage. As a
consequence they have so much wealth with which to corrupt
international standards of
safety that they now build them approximately without
safety factors__ergo, more and
more oil tanker wrecks and spills.
|
| Next Section: 1053.80 |