
 Cosmic Illions
Cosmic Illions

|
1231.00  Cosmic Illions
Cosmic Illions
|

|
1231.01
 Western-world humans are no longer spontaneously cognizant
of the Greek
or Latin number prefixes like dec-, or non-, or oct-,
nor are they able spontaneously to
formulate in appropriate Latin or Greek terms the larger
numbers spoken of by scientists
nowadays only as powers of ten. On the other hand, we
are indeed familiar with the
Anglo-American words one, two, and three, wherefore
we may prefix these more familiar
designations to the constant illion, suffix which we
will now always equate with a set of
three successive zeros. (See Table
1238.80.)
Western-world humans are no longer spontaneously cognizant
of the Greek
or Latin number prefixes like dec-, or non-, or oct-,
nor are they able spontaneously to
formulate in appropriate Latin or Greek terms the larger
numbers spoken of by scientists
nowadays only as powers of ten. On the other hand, we
are indeed familiar with the
Anglo-American words one, two, and three, wherefore
we may prefix these more familiar
designations to the constant illion, suffix which we
will now always equate with a set of
three successive zeros. (See Table
1238.80.)
|

|
1231.02
 We used to call 1,000 one thousand. We will now call
it oneillion. Each
additional set of three zeros is recognized by the prefixed
number of such three-zero sets.
1,000,000= two-illion. 1,000,000,000 is 1 three-illion.
(This is always hyphenated to avoid
confusion with the set of subillion enumerators, e.g.,
206 four-illions.) The English
identified illions only with six zero additions, while
the Americans used illions for every
three zeros, starting, however, only after 1,000, overlooking
its three zeros as common to
all of them. Both the English and American systems thus
were forced to use awkward
nomenclature by retaining the initial word thousand
as belonging to a different concept
and an historically earlier time. Using our consistent
illion nomenclature, we express the
largest experientially conceivable measurement, which
is the diameter of the thus-far-
observed Universe measured in diameters of the nucleus
of the atom, which measurement
is a neat 312 fourteenillions. (See Sec.
1238.50.)
We used to call 1,000 one thousand. We will now call
it oneillion. Each
additional set of three zeros is recognized by the prefixed
number of such three-zero sets.
1,000,000= two-illion. 1,000,000,000 is 1 three-illion.
(This is always hyphenated to avoid
confusion with the set of subillion enumerators, e.g.,
206 four-illions.) The English
identified illions only with six zero additions, while
the Americans used illions for every
three zeros, starting, however, only after 1,000, overlooking
its three zeros as common to
all of them. Both the English and American systems thus
were forced to use awkward
nomenclature by retaining the initial word thousand
as belonging to a different concept
and an historically earlier time. Using our consistent
illion nomenclature, we express the
largest experientially conceivable measurement, which
is the diameter of the thus-far-
observed Universe measured in diameters of the nucleus
of the atom, which measurement
is a neat 312 fourteenillions. (See Sec.
1238.50.)
|

|
1232.00
 Binomial Symmetry of Scheherazade Numbers
Binomial Symmetry of Scheherazade Numbers
|

|
1232.10
 Exponential Powers of 1,001: As with all binomials,
for example A2 + 2AB
+B2, the progressive powers of the 1,001 Scheherazade
Number produced by 7 × 11 ×
the product of which, multiplied by itself in successive
stages, provides a series of
symmetrical reflection numbers. They are not only sublimely
rememberable but they
resolve themselves into a symmetrical mirror pyramid
array:
Exponential Powers of 1,001: As with all binomials,
for example A2 + 2AB
+B2, the progressive powers of the 1,001 Scheherazade
Number produced by 7 × 11 ×
the product of which, multiplied by itself in successive
stages, provides a series of
symmetrical reflection numbers. They are not only sublimely
rememberable but they
resolve themselves into a symmetrical mirror pyramid
array:
|

|
1232.11
 The binomial symmetry expands all of its multiples
in both left and right
directions in reflection balance. Note that the exponential
power to which the 1,001
Scheherazade Number is raised becomes the second whole
integer from either end. As
with (A+B)2 = A2 + 2AB + B2, the interior integers consist
of expressions and products of
the exponent power.
The binomial symmetry expands all of its multiples
in both left and right
directions in reflection balance. Note that the exponential
power to which the 1,001
Scheherazade Number is raised becomes the second whole
integer from either end. As
with (A+B)2 = A2 + 2AB + B2, the interior integers consist
of expressions and products of
the exponent power.
|

|
1232.20
 Cancellation of "Leftward Spillover": In the pyramid
array of 1,001
Scheherazade Numbers (see Sec.
1232.10), we observe
that due to the double-symbol
notation of the number 10, the symmetry seems to be
altered by the introduction of the
leftward accommodation of the two integers of 10 in
a single-integer position. For
instance,
Cancellation of "Leftward Spillover": In the pyramid
array of 1,001
Scheherazade Numbers (see Sec.
1232.10), we observe
that due to the double-symbol
notation of the number 10, the symmetry seems to be
altered by the introduction of the
leftward accommodation of the two integers of 10 in
a single-integer position. For
instance,
Ten could be written vertically as
|
 Table 1232.21 |
1232.21
 The abacus with its wires and beads taught humans how
to fill a column with
figures and thereafter to fill additional columns, by
convention to the left. The Arabic
numerals developed as symbols for the content of the
columns. They filled a column and
then they emptied it, but the cipher prevented them
from using the column for any other
notation, and the excess__by convention__was moved over
to the left. This ''spillover" can
begin earlier or later, depending on the modulus employed.
The spillover to the next
column begins later when we are employing Modulo 12
than when we are employing
Modulo 10. To disembarrass the symmetry of the leftward
spillover, the spillover number
in the table has been written vertically.
The abacus with its wires and beads taught humans how
to fill a column with
figures and thereafter to fill additional columns, by
convention to the left. The Arabic
numerals developed as symbols for the content of the
columns. They filled a column and
then they emptied it, but the cipher prevented them
from using the column for any other
notation, and the excess__by convention__was moved over
to the left. This ''spillover" can
begin earlier or later, depending on the modulus employed.
The spillover to the next
column begins later when we are employing Modulo 12
than when we are employing
Modulo 10. To disembarrass the symmetry of the leftward
spillover, the spillover number
in the table has been written vertically.
|

|
1232.22
 The table of the ten successive powers of the 1,001
Scheherazade Number
accidentally discloses a series of progressions:
The table of the ten successive powers of the 1,001
Scheherazade Number
accidentally discloses a series of progressions:
|

|
1232.23
 The tetrahedron can be symmetrically or asymmetrically
altered to
accommodate the four unique planes that produce the
fourth-dimensional accommodation
of the vector equilibrium. The symmetry disclosed here
may very well be four-dimensional
symmetry that we have simply expressed in columns in
a plane.
The tetrahedron can be symmetrically or asymmetrically
altered to
accommodate the four unique planes that produce the
fourth-dimensional accommodation
of the vector equilibrium. The symmetry disclosed here
may very well be four-dimensional
symmetry that we have simply expressed in columns in
a plane.
|

|
1232.24
 The number 1,001 looks exciting because we are very
close to the binary
system of the computers. (We remember that Polynesians
only counted to one and two.)
The binary yes-no sequence looks so familiar. The Scheherazade
Number has all the
numbers you have in the binary system. The l,001-ness
keeps persisting throughout the
table.
The number 1,001 looks exciting because we are very
close to the binary
system of the computers. (We remember that Polynesians
only counted to one and two.)
The binary yes-no sequence looks so familiar. The Scheherazade
Number has all the
numbers you have in the binary system. The l,001-ness
keeps persisting throughout the
table.
|

|
1232.25
 The numbers 7 × 11 × 13 × 17 included in the symmetric
dividend 510,510
may have an important function in atomic nucleation,
since it accommodates all the prime
numbers involved in the successive periods.
The numbers 7 × 11 × 13 × 17 included in the symmetric
dividend 510,510
may have an important function in atomic nucleation,
since it accommodates all the prime
numbers involved in the successive periods.
|

|
1232.26
 Many mathematicians assume that the integer 1 is not
to be counted as a
prime. Thus 2, 3, 5, 7, 11, and 13 make a total of six
effective primes that may be
identified with the fundamental vector edges of the
tetrahedron and the six axes of
conglomeration of 12 uniradius spheres closest packed
around one nuclear sphere, and the
fundamental topological abundance of universal lines
that always consist of even sets of
six.
Many mathematicians assume that the integer 1 is not
to be counted as a
prime. Thus 2, 3, 5, 7, 11, and 13 make a total of six
effective primes that may be
identified with the fundamental vector edges of the
tetrahedron and the six axes of
conglomeration of 12 uniradius spheres closest packed
around one nuclear sphere, and the
fundamental topological abundance of universal lines
that always consist of even sets of
six.
|

|
1232.30
 Scheherazade Reflection Patterns:
Scheherazade Reflection Patterns:
|

|
1234.00
 Seven-illion Scheherazade Number
Seven-illion Scheherazade Number
|

|
1234.01
 The Seven-illion Scheherazade Number includes the first
seven primes,
which are:
The Seven-illion Scheherazade Number includes the first
seven primes,
which are:
(1·2·3·5·7·11·13)5 ... to the fifth power.
It reads,
24,421,743,243,121,524,300,000
|

|
1234.02
 In the first days of electromagnetics, scientists discovered
fourth-power
energy relationships and Einstein began to find fifth-power
relationships having to do with
gravity accommodating fourth- and fifth-powering. The
first seven primes factorial is a
sublimely rememberable number. It is a big number, yet
rememberable. When nature gives
us a number we can remember, she is putting us on notice
that the cosmic communications
circuits are open: you are connected through to many
sublime truths!
In the first days of electromagnetics, scientists discovered
fourth-power
energy relationships and Einstein began to find fifth-power
relationships having to do with
gravity accommodating fourth- and fifth-powering. The
first seven primes factorial is a
sublimely rememberable number. It is a big number, yet
rememberable. When nature gives
us a number we can remember, she is putting us on notice
that the cosmic communications
circuits are open: you are connected through to many
sublime truths!
|

|
1234.03
 Though factored by seven prime numbers, it is expressible
entirely as
various-sized increments of three to the fifth power.
There is a four-place overlapping of
one. Three to the fifth power means five-dimensionality
triangulation, which means that
five-dimensional structuring as triangulation is structure.
Though factored by seven prime numbers, it is expressible
entirely as
various-sized increments of three to the fifth power.
There is a four-place overlapping of
one. Three to the fifth power means five-dimensionality
triangulation, which means that
five-dimensional structuring as triangulation is structure.
|

|
1234.04
 When it is substituted as a comprehensive dividend
for 360° 00' 00" to
express cyclic unity in increments equal to one second
of arc, while recalculating the tables
of trigonometric functions, it is probable that many,
if not most, and possibly all the
function fractions will be expressible as whole rational
numbers. The use of
24,421,743,243,121,524,300,000 as cyclic unity will
eliminate much cumulative error of
the present trigonometric-function tables.
When it is substituted as a comprehensive dividend
for 360° 00' 00" to
express cyclic unity in increments equal to one second
of arc, while recalculating the tables
of trigonometric functions, it is probable that many,
if not most, and possibly all the
function fractions will be expressible as whole rational
numbers. The use of
24,421,743,243,121,524,300,000 as cyclic unity will
eliminate much cumulative error of
the present trigonometric-function tables.
|

|
1234.10
 Seven-illion Scheherazade Number: Symmetrical Mirror
Pyramid Array
Seven-illion Scheherazade Number: Symmetrical Mirror
Pyramid Array
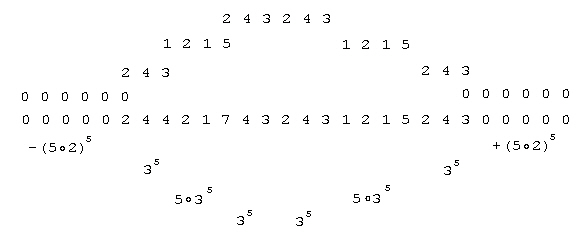
where 35 = 243, 5·35 = 1215, -(5·2)5 = five zero prefix, + (5·2)5 = five zero sufix |

|
1236.00
 Eight-illion Scheherazade Number
Eight-illion Scheherazade Number
|

|
1236.01
 The Eight-illion Scheherazade Number is
The Eight-illion Scheherazade Number is
It reads:
1,452,803,177,020,770,377,302,500
|

|
1236.02
 The Eight-illion Scheherazade Number accommodates all
trigonometric
functions, spherical and planar, when unity is 60 degrees;
its halfway turnabout is 30
degrees. It also accommodates the octave-nine-zero of
the icosahedron's corner angles of
72 degrees, one-half of which is 36 degrees (ergo, 31
is the greatest prime involved),
which characterizes maximum spherical excess of the
vector equilibrium's sixty-
degreeness.
The Eight-illion Scheherazade Number accommodates all
trigonometric
functions, spherical and planar, when unity is 60 degrees;
its halfway turnabout is 30
degrees. It also accommodates the octave-nine-zero of
the icosahedron's corner angles of
72 degrees, one-half of which is 36 degrees (ergo, 31
is the greatest prime involved),
which characterizes maximum spherical excess of the
vector equilibrium's sixty-
degreeness.
|

|
1237.00
 Nine-illion Scheherazade Number
Nine-illion Scheherazade Number
|

|
1237.01
 The Nine-illion Scheherazade Number includes the first
12 primes, which
are:
The Nine-illion Scheherazade Number includes the first
12 primes, which
are:
185,958,806,658,658,608,294,720,000,000
It is full of mirrors:

|

|
1238.00
 Fourteen-illion Scheherazade Number
Fourteen-illion Scheherazade Number
|

|
1238.20
 Trigonometric Limit: First 14 Primes: The Fourteen-illion
Scheherazade
Number accommodates all the omnirational calculations
of the trigonometric function
tables whose largest prime number is 43 and whose highest
common variable multiple is
45 degrees, which is one-eighth of unity in a Universe
whose polyhedral systems consist
always of a minimum of four positive and four negative
quadranted hemispheres.
Trigonometric Limit: First 14 Primes: The Fourteen-illion
Scheherazade
Number accommodates all the omnirational calculations
of the trigonometric function
tables whose largest prime number is 43 and whose highest
common variable multiple is
45 degrees, which is one-eighth of unity in a Universe
whose polyhedral systems consist
always of a minimum of four positive and four negative
quadranted hemispheres.
|

|
1238.21
 45 degrees is the zero limit of covarying asymmetry
because the right
triangle's 90-degree corner is always complemented by
two corners always together
totalling 90 degrees. The smallest of the covarying,
90-degree complementaries reaches its
maximum limit when both complementaries are 45 degrees.
Accepting the concept that
one is not a prime number, we have 14 primes__2, 3, 5,
7, 11, 13, 17, 19, 23, 29, 31, 37,
41, 43__which primacy will accommodate all the 14 unique
structural faceting of all the
crystallography, all the biological cell structuring,
and all bubble agglomerating: the 14
facets being the polar facets of the seven and only
seven axes of symmetry of Universe,
which are the 3-, 4-, 6-, 12-great circles of the vector
equilibrium and the 6-, 10-, 15-great
circles of the icosahedron.
45 degrees is the zero limit of covarying asymmetry
because the right
triangle's 90-degree corner is always complemented by
two corners always together
totalling 90 degrees. The smallest of the covarying,
90-degree complementaries reaches its
maximum limit when both complementaries are 45 degrees.
Accepting the concept that
one is not a prime number, we have 14 primes__2, 3, 5,
7, 11, 13, 17, 19, 23, 29, 31, 37,
41, 43__which primacy will accommodate all the 14 unique
structural faceting of all the
crystallography, all the biological cell structuring,
and all bubble agglomerating: the 14
facets being the polar facets of the seven and only
seven axes of symmetry of Universe,
which are the 3-, 4-, 6-, 12-great circles of the vector
equilibrium and the 6-, 10-, 15-great
circles of the icosahedron.
|

|
1238.22
 Tetrahedral Complementations The sphere-to-space, space-to-sphere
intertransformability is a conceptual generalization
holding true independent of size, which
therefore permits us to consider the generalized allspace-filling
complementarity of the
convex (sphere) and concave (space) octahedra with the
convex (sphere) and concave
(space) vector equilibria; this also permits us to indulge
our concentrated attention upon
local special-case events without fear of missing further
opportunities of enjoying total
synergetically conceptual advantage regarding nonsimultaneously
considerable Scenario
Universe. (See Secs.
970.20
and
1032.)
Tetrahedral Complementations The sphere-to-space, space-to-sphere
intertransformability is a conceptual generalization
holding true independent of size, which
therefore permits us to consider the generalized allspace-filling
complementarity of the
convex (sphere) and concave (space) octahedra with the
convex (sphere) and concave
(space) vector equilibria; this also permits us to indulge
our concentrated attention upon
local special-case events without fear of missing further
opportunities of enjoying total
synergetically conceptual advantage regarding nonsimultaneously
considerable Scenario
Universe. (See Secs.
970.20
and
1032.)
|

|
1238.23
 We know the fundamental intercomplementations of the
external convex
macrotetra and the internal concave microtetra with
all conceptual systems. Looking at the
four successive plus, minus, plus, minus, XYZ coordination
quadrants, we find that a
single 90-degree quadrant of one hemisphere of the spherical
octahedron contains all the
trigonometric functioning covariations of the whole
system. When the central angle is 90
degrees, then the two small corner angles of the isosceles
triangle are each 45 degrees.
After 45 degrees the sines become cosines, and vice
versa. At 45 degrees they balance.
Thereafter all the prime numbers that can ever enter
into prime trigonometric computation
(in contradistinction to complementary function computation)
occur below the number 45.
What occasions irrationality is the inability of dividends
to be omni-equi-divisible, due to
the presence of a prime number of which the dividend
is not a whole product.
We know the fundamental intercomplementations of the
external convex
macrotetra and the internal concave microtetra with
all conceptual systems. Looking at the
four successive plus, minus, plus, minus, XYZ coordination
quadrants, we find that a
single 90-degree quadrant of one hemisphere of the spherical
octahedron contains all the
trigonometric functioning covariations of the whole
system. When the central angle is 90
degrees, then the two small corner angles of the isosceles
triangle are each 45 degrees.
After 45 degrees the sines become cosines, and vice
versa. At 45 degrees they balance.
Thereafter all the prime numbers that can ever enter
into prime trigonometric computation
(in contradistinction to complementary function computation)
occur below the number 45.
What occasions irrationality is the inability of dividends
to be omni-equi-divisible, due to
the presence of a prime number of which the dividend
is not a whole product.
|

|
1238.24
 This is why we factor completely or intermultiply all
of the first 14 prime
numbers existing between 1 and 45 degrees. Inclusive
of these 14 numbers we multiply the
first eight primes to many repowerings, which produces
this Scheherazade Number,
which, when used as the number of units in a circle,
becomes a dividend permitting
omnirational computation accommodation of all the variations
of all the trigonometries of
Universe.
This is why we factor completely or intermultiply all
of the first 14 prime
numbers existing between 1 and 45 degrees. Inclusive
of these 14 numbers we multiply the
first eight primes to many repowerings, which produces
this Scheherazade Number,
which, when used as the number of units in a circle,
becomes a dividend permitting
omnirational computation accommodation of all the variations
of all the trigonometries of
Universe.
|

|
1238.25
 The four vertexial stars A, B, C, D defining the minimum
structural__ergo,
triangulated__system of Universe have only four possible
triangular arrangements. There
are only four possible different topological vertex
combinations of a minimum structural
system: ABC, ABD, ACD, BCD. In multifrequenced, modular
subdivisioning of the
minimum structural system, the subdividing grid may
develop eight positive and negative
aspects:
The four vertexial stars A, B, C, D defining the minimum
structural__ergo,
triangulated__system of Universe have only four possible
triangular arrangements. There
are only four possible different topological vertex
combinations of a minimum structural
system: ABC, ABD, ACD, BCD. In multifrequenced, modular
subdivisioning of the
minimum structural system, the subdividing grid may
develop eight positive and negative
aspects:
|
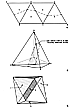 Fig. 1238.26 |
1238.26
 Three unopened edges AB, AD, BC. (Fig.
1238.26A.)
Three unopened edges AB, AD, BC. (Fig.
1238.26A.)
Four edge-bonded triangles of the tetrahedron. (Fig. 1238.26B.) Three pairs of opened edges; three pairs of unopened edges. Each triangle has also both obverse and reverse surfaces; ergo, minimum closed system of Universe has four positive and four negative triangles__which equals eight cases of the same. The same four triangles vertex-bond to produce the octahedron. (Fig. 1238.26C.) |

|
1238.27
 In a spherically referenced symmetrical structural
system one quadrant of
one hemisphere contains all the trigonometric variables
of the whole system. This is
because each hemisphere constitutes a 360-degree encirclement
of its pole and because a
90-degree quadrant is represented by three equi-right-angle
surface-angle corners and
three equi-90-degree central-angle-arc edges, half of
which 90-degree surface and central
angles is 45 degrees, which is the point where the sine
of one angle becomes the cosine of
the other and knowledge of the smallest is adequate__ergo,
45° 45° is the limit case of the
smallest.
In a spherically referenced symmetrical structural
system one quadrant of
one hemisphere contains all the trigonometric variables
of the whole system. This is
because each hemisphere constitutes a 360-degree encirclement
of its pole and because a
90-degree quadrant is represented by three equi-right-angle
surface-angle corners and
three equi-90-degree central-angle-arc edges, half of
which 90-degree surface and central
angles is 45 degrees, which is the point where the sine
of one angle becomes the cosine of
the other and knowledge of the smallest is adequate__ergo,
45° 45° is the limit case of the
smallest.
|

|
1238.28
 Spherical Quadrant Phase: There is always a total of
eight (four positive,
four negative) unique
Spherical Quadrant Phase: There is always a total of
eight (four positive,
four negative) unique
phases of all cyclically described symmetrical systems (see Sec. 610.20), within any one octave of which all the intercovariable ranging complementations of number occur. For instance, in a system such as spherical trigonometry, consisting of 360 degrees per circle or cycle, all the numerical intervariabilities occur within the first 45 degrees, .: 45 × 8 = 360. Since the unit cyclic totality of the Fourteen-illion Scheherazade Number is the product of the first 15 primes, it contains all the prime numbers occurring within the 45- degree-limit numerical integer permutations of all cyclic systems together with an abundance of powers of the first eight primes, thus accommodating omnirational integrational expressibility to a 1 × 10-42 fraction of cyclic unity, a dividend so comprehensive as to permit the rational description of a 22 billion-light-year-diameter Universe in whole increments of 1/10,000ths of one atomic nucleus diameter. |

|
1238.29
|
| Next Section: 1238.30 |