714.00 Interstabilization of Local Stiffeners
714.01 Local, Discontinuous, Compressional Strut Waves Interstabilizing Two Concentric, Differentially Radiused Tensegrity Spheres: Highly stable, nonredundant, rigidly trussed, differently radiused, concentric spherical tensegrity structures of hexagonal-pentagonal, inner or outer (but not both) surface dimples, symmetrically interspersing their omnitriangularly interlinked, spherically closed systems, may be constructed with swaged crossings of high-tensile-steel-cabled, spherical nets and locally islanded compressional struts occurring discontinuously as inbound-outbound, triangularly intertrussing, locally islanded compressional struts. The struts may then be either hydraulically actuated to elongate them to designed dimensions, or may be locally jacked in between the comprehensively prefabricated, spherical-system tensional network.
714.02 The local struts are so oriented that they always and only angle inwardly and outwardly between the concentric, differently radiused, comprehensively finite, exterior and interior, tensional spherical nets. The result is an interstabilized dynamic equilibrium of positive and negative waves of action. Such tensegrity sphere structures are limited in size only by the day-to-day limits of industrial production and service-logistics techniques. Large tensegrity spheres can have their lower portions buried in reinforced-concrete as tie- down bases to secure them against hurricane-drag displacement.
715.00 Locked Kiss
715.01 As we increase the frequency of triangular-module subdivisions of a tensegrity geodesic sphere, we thus also increase the number of compression struts, which get progressively halved in length, while their volumes and weights shrink eightfold. At the same time, the arc altitude between the smaller arcs and chords of the sphere decreases, while the compression members get closer and closer to the adjacent compression members they cross. Finally, we reach the condition where the space between the struts is the same dimension as the girth radius of the struts. At this point, we can let them kiss- touch; i.e., with the ends of two converging struts contacting the top middle of the strut running diagonally to those two struts and immediately below their ends. We may then lock the three kissing members tensionally together in their kiss, but when we do so, we must remember that they were not pushing one another when they "kissed" and we locked them in that equilibrious, "most comfortable" position of contact coincidence. Tensegrity spheres are not fastened in shear, even though their locked kiss gives a superficially "solid" continuity appearance that is only subvisibly discontinuous at the atomic level.
716.00 Complex Continuity and Discontinuity in Tensegrity Structures

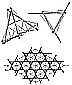Fig. 716.01 		716.01 The terminal junctures of four three-strut tensegrity octahedra are all 180- degree junctures. They appear to be compressionally continuous, while the central coherence of the three struts appears visibly discontinuous. The complex tensegrity presents a visibly deceptive appearance to the unwary observer. The two joined legs of the basic units appear as single units; as such, they appear to be primary elements of the complex tensegrity, whereas we learn from construction that our elements are the three- strut octahedra and that the cohering principle of the simplest elements is tensegrity.
716.02 The fundamental, repeatable unit used to form the spherical tensegrity structures is a flattened form of the basic three-strut tensegrity octahedron.
716.03 The basic 12-frequency tensegrity matrix employs collections of the basic three-strut units joined at dead center between single- and double-bonded discontinuity. The shaded triangles in the illustration represent the sites for each of the three-strut units. This matrix is applied to the spherical triacontrahedron__consequently, the large 12- frequency rhombus (illustration 716.01C) is one-thirtieth of the entire sphere.
716.10 Convergence
716.11 Whereas man seems to be blind in employing tensegrity at his level of everyday consciousness, we find that tensegrity structures satisfy our conceptual requirement that we may not have two events passing through the same point at the same time. Vectors converge in tensegrity, but they never actually get together; they only get into critical proximities and twist by each other.
717.00 Single- and Double-Bonding in Tensegrity Spheres

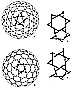Fig. 717.01 		717.01 Basic three-strut tensegrities may be joined in single-bonding or double- bonding to form a complex, 270-strut, isotropic tensegrity geodesic sphere. It can be composited to rotate negatively or positively. A six-frequency triacontrahedron tensegrity is shown in illustration 717.01.
717.02 Complexes of basic three-strut tensegrities are shown with axial alignment of exterior terminals to be joined in single bond as a 90-strut tensegrity.

720.00 Basic Tensegrity Structures

720.01 In basic tensegrity structures, the spheric-tension network system is completely continuous. The ends of each compression member connect only with the tension network at various points on the tensional catenaries nearest to the respective ends of the system's omni-islanded compression vector struts. The tension members running between the ends of the struts may be double or single. Double tension members best distribute the loads and most economically and nonredundantly accommodate the omnidistributive stress flows of the system. The catenaries always yield in obtuse or acute "V" shapes at their points of contact with the strut islands of compression.
720.02 Conventional building with continuous compression and discontinuous tension is accustomed to fastening compression members to their buildings in shear, that is, in predictably, calculatable, "slide-by" pushing actions, where one force opposes another in parallel but opposite directions.
720.03 But in tensegrity structures, the tension members pull away from the compression strut ends, which the V-shape tension connections demonstrate. If two people take positions on opposite sides of a tensegrity sphere and pull on polarly opposite struts in opposite directions from one another, it will be seen that all around the sphere there is a uniform and symmetrical response to the opposite pulling (or pushing). Pulling on two opposite parts makes the whole sphere grow symmetrically in size, while pushing forces the whole sphere to shrink contractively and symmetrically. Cessation of either the pulling or the pushing causes the sphere to take its size halfway between the largest and smallest conditions, i.e., in its equilibrious size. This phenomenon is a typical four- dimensional behavior of synergetic intertransforming. It explains why it is that all local celestial systems of Universe, being cohered with one another tensionally, pull on one another to bring about an omniexpanding physical Universe.
720.10 Micro-Macro Structural Model: If you just tauten one point in a tensegrity system, all the other parts of it tighten evenly. If you twang any tension member anywhere in the structure, it will give the same resonant note as the others. If you tauten any one part, the tuning goes to a higher note everywhere in the structure. Until its tension is altered, each tensegrity structure, as with every chemical element, has its own unique frequency. In a two-sling tensegrity sphere, every part is nonredundant. If tension goes up and the frequency goes up, it goes up uniformly all over. As tensegrity systems are tautened, they approach but never attain rigidity, being nonredundant structures. Anything that we would call rigid, such as one of the atoms of a very high integrity pattern, is explained by this type of tensegrity patterning.
720.11 The kinetically interbalanced behaviors of tensegrity systems manifest discretely and elucidate the energy-interference-event patternings that integrate to form and cohere all atoms. The tensegrity system is always the equilibrious-balance phase, i.e., the omnipotential-energy phase visually articulate of the push-pull, in-out-and-around, pulsating and orbiting, precessionally shunted reangulations, synergetically integrated.
720.12 The circumferentially islanded tensegrity struts are energy vectors in action, and the tension lines are the energy tensors in action. Their omnisystem interpatterning shows how the circumferentially orbiting tensegrity struts' lead ends are pulled by the center of mass of the next adjacent inwardly positioned vector strut. The mass attraction pulls inwardly on the lead ends of the precessionally articulating, self-orbiting, great-circle chord vector struts, thus changing their circumferential direction. They are precessionally and successively deflected from one tangent course to the next, circumferentially inward and onward, tangent vector course. Thus each of the vectors is successively steered to encircle the same tensegrity system center. In this manner, a variety of energy-interference, kinetic-equilibrium patterns results in a variety of cosmically local, self-regenerative, micro-macro structural systems such as atoms or star systems.
721.00 Stability Requires Six Struts
721.01 Stability requires six struts, each of which is a combinedly push-pull structural member. It is a synergetic (Sec. 101) characteristic of minimum structural (Sec. 610) systems (Sec. 402) that the system is not stable until the introduction of the last structural component (Sec. 621.10) essential to completion of minimum omnisymmetric array.
721.02 Redundancy (Sec. 723) can be neither predicted nor predetermined by observation of either the integral constraints or external freedoms of energetic behaviors of single struts, or beams, or columns, or any one chain link of a series that is less than 12 in number, i.e., six positive vectors and six negative tensors. Of these 12, six are open- endedly uncoordinate, disintegrative forces that are always omni-cohered by six integrative forces in finitely closed coordination.
722.00 Push-Pull Members
722.01 Minimum structural-system stability requires six struts, each of which is a push-pull member. Push-pull structural members embody in one superficially solid system both the axial-linear tension and compression functions.
722.02 Tensegrity differentiates out these axial-linears into separately cofunctioning compression vectors and tensional tensors. As in many instances of synergetic behavior, these differentiations are sometimes subtle. For instance, there is a subtle difference between Eulerian topology, which is polyhedrally superficial, and synergetic topology, which is nuclear and identifies spheres with vertexes, solids with faces, and struts with edges. The subtlety lies in the topological differentiation of the relative abundance of these three fundamental aspects whereby people do not look at the four closest-packed spheres forming a tetrahedron in the same way that they look at a seemingly solid stone tetrahedron, and quite differently again from their observation of the six strut edges of a tetrahedron, particularly when they do not accredit Earth with providing three of the struts invisibly cohering the base ends of the camera tripod.
723.00 Redundance
723.01 There are metaphysical redundancies, repeating the same thing, saying it in a little different way each time.
723.02 There are physical redundancies when, for instance, we have a mast stepped in a hole in the ground and three tensional stays at 120 degrees. When a fourth tension member is led to an anchor at an equiradiused distance from the mast base and at one degree of circular arc away from one of the original three anchors, we then have two tension stays running side by side. When the two stays are thus approximately parallel, we find it is impossible to equalize the tensions exactly. One or the other will get the load, not both .
723.03 It is structural redundancy when a square knot is tied and an amateur says, "I'm going to make that stronger by tying more square knots on top of it." The secondary knots are completely ineffective because the first square knot will not yield. There is a tendency of the second square knot to "work open" and thus deteriorate the first knot. Structural redundancies tend to deteriorate the effectiveness of the primary members.
723.04 There are two classes of redundant acts:
  1. conscious and knowledgeably competent, and
  2. subconscious and ignorantly fearful cautionaries.
723.05 Building codes of cities, formulated by politicians fearful of the calumny of what may befall them if buildings fall down, ignorantly insist on doubling the thickness of walls. Building codes require a safety factor of usually five, or more, to one.
723.06 Aircraft designing employs a safety factor of two to one__or even no safety factor at all, while cautioning the pilot through instrumental indication of when he is approaching limit condition. The deliberately imposed safety factors of society's building conglomerates introduce redundancy breeding redundancy, wherein__as with nuclear fusion, chain-reacting__the additional weights to carry the additional weights multiply in such a manner as to increase the inefficiency imposed by the redundancy at an exponential rate implicit in Newton's mass-attraction gravitational law: every time we double the safety factor, we fourfold the inefficiency and eightfold the unnecessary weight.
724.00 Three and Only Basic Structures
724.01 The original six vector-edge members of the tensegrity tetrahedron may be transformed through the tensegrity-octahedron phase and finally into the tensegrity- icosahedron phase. The same six members transform their relation to each other through the full range of the three (only) fundamental structures of nature: the tetrahedron, the octahedron, and the icosahedron. (See Secs. 532.40, 610.20, 724, 1010.20, 1011.30 and 1031.13.)
724.02 The same six members transform from containing one volume to containing 18.51 volumes. These are the principles actively operative in atomic-nucleus behavior in visual intertransformations.

Fig. 724.10 		724.10 Tensegrity Octahedron: The simplest form of tensegrity is the octahedron with three compression members crossing each other. The three compression struts do not touch each other as they pass at the center. They are held together only at their terminals by the comprehensive triangular tension net. The same three-islanded struts of the tensegrity octahedron may be mildly reorganized or asymmetrically transformed.
724.11 The struts may be the same length or of different lengths. Some tensional edges may be lengthened while other tensional edges of the surface triangles are shortened. The compression members still do not touch each other. One figure is a positive and the other a negative tensegrity octahedron. They can be joined together to make a new form: the tensegrity icosahedron.
724.20 Tensegrity Icosahedron: The six-islanded-strut icosahedron and its allspace-filling, closest-packing capability provide omni-equi-optimum economy tensegrity Universe structuring.

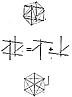Fig. 724.30 		724.30 Six-Strut Tensegrities: Two three-strut tensegrities may be joined together to make the tensegrity icosahedron. This form has six members in three parallel sets with their ends held together in tension. There are 12 terminals of the six struts (the two octahedra__each with three struts of six ends__combined). When you connect up these 12 terminals, you reveal the 12 vertexes of the icosahedron. There are 20 triangles of the icosahedron clearly described by the tension members connecting the 12 points in the most economical omnitriangular pattern.
724.31 In the tensegrity icosahedron, there are six tension members, which join parallel struts to each other. If these tension members are removed from the icosahedron, only eight triangles remain from the original 20. These eight triangles are the eight transforming triangles of the symmetrical contraction of the vector equilibrium "jitterbug." (See Sec. 460.) Consequently, this "incomplete" icosahedron demonstrates an expansion- contraction behavior similar to the "jitterbug," although pulsing symmetrically inward- outward within more restricted limits.
724.32 If two opposite and parallel struts are pushed or pulled upon, all six members will move inwardly or outwardly, causing the icosahedron to contract or expand in a symmetrical fashion. When this structure is fully expanded, it is the regular icosahedron; in its contracted state, it becomes an icosahedron bounded by eight equilateral triangles and 12 isosceles triangles (when the missing six tension members are replaced). All 12 vertexes may recede from the common center in perfect symmetry of expansion or, if concentrated load is applied from without, the whole system contracts symmetrically, i.e., all the vertexes move toward their common center at the same rate.
724.33 This is not the behavior we are used to in any structures of our previous experiences. These compression members do not behave like conventional engineering beams. Ordinary beams deflect locally or, if fastened terminally in tension to their building, tend to contract the building in axial asymmetry. The tensegrity "beam" does not act independently but acts only in concert with "the whole building," which contracts only symmetrically when the beam is loaded.
724.34 The tensegrity system is synergetic__a behavior of the whole unpredicted by the behavior of the parts. Old stone-age columns and lintels are energetic and only interact locally with whole buildings. The whole tensegrity-icosahedron system, when loaded oppositely at two diametric points, contracts symmetrically, and because it contracts symmetrically, its parts get symmetrically closer to one another; therefore, gravity increases as of the second power, and the whole system gets uniformly stronger. This is the way atoms behave.
Next Section: 725.00
Copyright © 1997 Estate of R. Buckminster Fuller