
 Triangular Spiral Events Form Polyhedra
Triangular Spiral Events Form Polyhedra

|
613.00  Triangular Spiral Events Form Polyhedra
Triangular Spiral Events Form Polyhedra
|
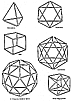 Fig. 613.01 |
613.01
 Open triangular spirals may be combined to make a
variety of different
figures. Note that the tetrahedron and icosahedron require
both left- and right-handed
(positive and negative) spirals in equal numbers, whereas
the other polyhedra require
spirals of only one-handedness. (See Sec.
452, Great
Circle Railroad Tracks of Energy.) If
the tetrahedron is considered to be one quantum, then
the triangular spiral equals one-half
quantum. It follows from this that the octahedron and
cube are each two quanta, the
icosahedron five quanta, and the two-frequency spherical
geodesic is 15 quanta.
Open triangular spirals may be combined to make a
variety of different
figures. Note that the tetrahedron and icosahedron require
both left- and right-handed
(positive and negative) spirals in equal numbers, whereas
the other polyhedra require
spirals of only one-handedness. (See Sec.
452, Great
Circle Railroad Tracks of Energy.) If
the tetrahedron is considered to be one quantum, then
the triangular spiral equals one-half
quantum. It follows from this that the octahedron and
cube are each two quanta, the
icosahedron five quanta, and the two-frequency spherical
geodesic is 15 quanta.
|

|
614.00
 Triangle
Triangle
|

|
614.01
 A triangle's three-vector parts constitute a basic
event. Each triangle consists
of three interlinked vectors. In the picture, we are
going to add one triangle to the other.
(See illustration
511.10.) In conventional arithmetic,
one triangle plus one triangle equals
two triangles. The two triangles represent two basic
events operating in Universe. But
experientially triangles do not occur in planes. They
are always omnidimensional positive
or negative helixes. You may say that we do not have
any right to break the triangles'
threesided rims open in order to add them together,
but the answer is that the triangles
were never closed, because no line can ever come completely
back "into" or "through"
itself. Two lines cannot be passed through a given point
at the same time. One will be
superimposed on the other. Therefore, the superimposition
of one end of a triangular
closure upon another end produces a spiral__a very flat
spiral, indeed, but openly
superimposed at each of its three corners, the opening
magnitude being within the critical
limit of mass attraction's 180-degree "falling-in" effect.
The triangle's open-ended ends
are within critical proximity and mass-attractively
intercohered, as are each and all of the
separate atoms in each of all the six separate structural
members of the necklace-structure
triangle. All coherent substances are "Milky Way" clouds
of critically proximate atomic
"stars."
A triangle's three-vector parts constitute a basic
event. Each triangle consists
of three interlinked vectors. In the picture, we are
going to add one triangle to the other.
(See illustration
511.10.) In conventional arithmetic,
one triangle plus one triangle equals
two triangles. The two triangles represent two basic
events operating in Universe. But
experientially triangles do not occur in planes. They
are always omnidimensional positive
or negative helixes. You may say that we do not have
any right to break the triangles'
threesided rims open in order to add them together,
but the answer is that the triangles
were never closed, because no line can ever come completely
back "into" or "through"
itself. Two lines cannot be passed through a given point
at the same time. One will be
superimposed on the other. Therefore, the superimposition
of one end of a triangular
closure upon another end produces a spiral__a very flat
spiral, indeed, but openly
superimposed at each of its three corners, the opening
magnitude being within the critical
limit of mass attraction's 180-degree "falling-in" effect.
The triangle's open-ended ends
are within critical proximity and mass-attractively
intercohered, as are each and all of the
separate atoms in each of all the six separate structural
members of the necklace-structure
triangle. All coherent substances are "Milky Way" clouds
of critically proximate atomic
"stars."
|

|
614.02
 Triangles are inherently open. As one positive event
and one negative event,
the two triangles arrange themselves together as an
interference of the two events. The
actions and the resultants of each run into the actions
and the resultants of the other. They
always impinge at the ends of the action as two interfering
events. As a tetrahedron, they
are fundamental: a structural system. It is a tetrahedron.
It is structural because it is
omnitriangulated. It is a system because it divides
Universe into an outsideness and an
insideness__into a macrocosm and a microcosm.
Triangles are inherently open. As one positive event
and one negative event,
the two triangles arrange themselves together as an
interference of the two events. The
actions and the resultants of each run into the actions
and the resultants of the other. They
always impinge at the ends of the action as two interfering
events. As a tetrahedron, they
are fundamental: a structural system. It is a tetrahedron.
It is structural because it is
omnitriangulated. It is a system because it divides
Universe into an outsideness and an
insideness__into a macrocosm and a microcosm.
|

|
614.03
 A triangle is a triangle independent of its edge-sizing.
A triangle is a triangle independent of its edge-sizing.
|

|
614.04
 Each of the angles of a triangle is interstabilized.
Each of the angles was
originally amorphous__i.e., unstable__but they become
stable because each edge of a
triangle is a lever. With minimum effort, the ends of
the levers control the opposite angles
with a push-pull, opposite-edge vector. A triangle is
the means by which each side
stabilizes the opposite angle with minimum effort.
Each of the angles of a triangle is interstabilized.
Each of the angles was
originally amorphous__i.e., unstable__but they become
stable because each edge of a
triangle is a lever. With minimum effort, the ends of
the levers control the opposite angles
with a push-pull, opposite-edge vector. A triangle is
the means by which each side
stabilizes the opposite angle with minimum effort.
|

|
614.05
 The stable structural behavior of a whole triangle,
which consists of three
edges and three individually and independently unstable
angles (or a total of six
components), is not predicted by any one or two of its
angles or edges taken by
themselves. A triangle (a structure) is synergetic:
it is a behavior of a whole unpredicted
by the behavior of any of its six parts considered only
separately.
The stable structural behavior of a whole triangle,
which consists of three
edges and three individually and independently unstable
angles (or a total of six
components), is not predicted by any one or two of its
angles or edges taken by
themselves. A triangle (a structure) is synergetic:
it is a behavior of a whole unpredicted
by the behavior of any of its six parts considered only
separately.
|

|
614.06
 When a bright light shines on a complex of surface
scratches on metal, we
find the reflection of that bright light upon the scratched
metal producing a complex of
concentric scratch-chorded circles. In a multiplicity
of omnidirectional actions in the close
proximity of the viewable depth of the surfaces, structurally
stable triangles are
everywhere resultant to the similarly random events.
That triangles are everywhere is
implicit in the fact that wherever we move or view the
concentric circles, they occur, and
that there is always one triangle at the center of the
circle. We could add the word
approximately everywhere to make the everywhereness
coincide with the modular-
frequency characteristics of any set of random multiplicity.
Because the triangles are
structurally stable, each one imposes its structural
rigidity upon its neighboring and
otherwise unstable random events. With energy operative
in the system, the dominant
strength of the triangles will inherently average to
equilateralness.
When a bright light shines on a complex of surface
scratches on metal, we
find the reflection of that bright light upon the scratched
metal producing a complex of
concentric scratch-chorded circles. In a multiplicity
of omnidirectional actions in the close
proximity of the viewable depth of the surfaces, structurally
stable triangles are
everywhere resultant to the similarly random events.
That triangles are everywhere is
implicit in the fact that wherever we move or view the
concentric circles, they occur, and
that there is always one triangle at the center of the
circle. We could add the word
approximately everywhere to make the everywhereness
coincide with the modular-
frequency characteristics of any set of random multiplicity.
Because the triangles are
structurally stable, each one imposes its structural
rigidity upon its neighboring and
otherwise unstable random events. With energy operative
in the system, the dominant
strength of the triangles will inherently average to
equilateralness.
|

|
614.07
 When we work with triangles in terms of total leverage,
we find that their
average, most comfortable condition is equilateral.
They tend to become equilateral.
Randomness of lines automatically works back to a set
of interactions and a set of
proximities that begin to triangulate themselves. This
effect also goes on in depth and into
the tetrahedra or octahedra.
When we work with triangles in terms of total leverage,
we find that their
average, most comfortable condition is equilateral.
They tend to become equilateral.
Randomness of lines automatically works back to a set
of interactions and a set of
proximities that begin to triangulate themselves. This
effect also goes on in depth and into
the tetrahedra or octahedra.
|

|
615.00
 Positive and Negative Triangulation of Cube and Vector
Equilibrium
Positive and Negative Triangulation of Cube and Vector
Equilibrium
|

|
615.01
 To be referred to as a rememberable entity, an object
must be membered
with structural integrity, whether maple leaf or crystal
complex. To have structural
integrity, it must consist entirely of triangles, which
are the only complex of energy events
that are self-interference-regenerating systems resulting
in polygonal pattern stabilization.
To be referred to as a rememberable entity, an object
must be membered
with structural integrity, whether maple leaf or crystal
complex. To have structural
integrity, it must consist entirely of triangles, which
are the only complex of energy events
that are self-interference-regenerating systems resulting
in polygonal pattern stabilization.
|

|
615.02
 A vectorial-edged cube collapses. The cube's corner
flexibility can be
frustrated only by triangulation. Each of the four corners
of the cube's six faces could be
structurally stabilized with small triangular gussets,
of which there would be 24, with the
long edge structurals acting as powerful levers against
the small triangles. The complete
standard stabilization of the cube can be accomplished
with a minimum of six additional
members in the form of six structural struts placed
diagonally, corner to comer, in each of
the six square faces, with four of the cube's eight
corner vertexes so interconnected. These
six, end-interconnected diagonals are the six edges
of a tetrahedron. The most efficiently
stabilized cubical form is accomplished with the prime
structural system of Universe: the
tetrahedron.
A vectorial-edged cube collapses. The cube's corner
flexibility can be
frustrated only by triangulation. Each of the four corners
of the cube's six faces could be
structurally stabilized with small triangular gussets,
of which there would be 24, with the
long edge structurals acting as powerful levers against
the small triangles. The complete
standard stabilization of the cube can be accomplished
with a minimum of six additional
members in the form of six structural struts placed
diagonally, corner to comer, in each of
the six square faces, with four of the cube's eight
corner vertexes so interconnected. These
six, end-interconnected diagonals are the six edges
of a tetrahedron. The most efficiently
stabilized cubical form is accomplished with the prime
structural system of Universe: the
tetrahedron.
|

|
615.03
 Because of the structural integrity of the blackboard
or paper on which they
may be schematically pictured, the cubically profiled
form can exist, but only as an
experienceable, forms-suggesting picture, induced by
lines deposited in chalk, or ink, or
lead, accomplished by the sketching individual with
only 12 of the compression-
representing strut edge members interjoined by eight
flexible vertex fastenings.
Because of the structural integrity of the blackboard
or paper on which they
may be schematically pictured, the cubically profiled
form can exist, but only as an
experienceable, forms-suggesting picture, induced by
lines deposited in chalk, or ink, or
lead, accomplished by the sketching individual with
only 12 of the compression-
representing strut edge members interjoined by eight
flexible vertex fastenings.
|

|
615.04
 The accomplishment of experienceable, structurally
stabilized cubes with a
minimum of nonredundant structural components will always
and only consist of one
equiangled and equiedged "regular" tetrahedron on each
of whose four faces are
congruently superimposed asymmetrical tetrahedra, one
of whose four triangular faces is
equiangled and therefore congruently superimposable
on each of the four faces of the
regular tetrahedron; while the four asymmetrical superimposed
tetrahedra's other three
triangular__and outwardly exposed__faces are all similar
isosceles triangles, each with
two 45-degree-angle corners and one corner of 90 degrees.
Wherefore, around each of the
outermost exposed corners of the asymmetrical tetrahedra,
we also find three 90-degree
angles which account for four of the cube's eight corners;
while the other four 90-degree
surrounded corners of the cube consist of pairs of 45-degree
corners of the four
asymmetric tetrahedra that were superimposed upon the
central regular tetrahedron to
form the stabilized cube. More complex cubes that will
stand structurally may be
compounded by redundant strutting or tensioning triangles,
but redundancies introduce
microinvisible, high- and low-frequency, self-disintegrative
accelerations, which will
always affect structural enterprises that overlook or
disregard these principles.
The accomplishment of experienceable, structurally
stabilized cubes with a
minimum of nonredundant structural components will always
and only consist of one
equiangled and equiedged "regular" tetrahedron on each
of whose four faces are
congruently superimposed asymmetrical tetrahedra, one
of whose four triangular faces is
equiangled and therefore congruently superimposable
on each of the four faces of the
regular tetrahedron; while the four asymmetrical superimposed
tetrahedra's other three
triangular__and outwardly exposed__faces are all similar
isosceles triangles, each with
two 45-degree-angle corners and one corner of 90 degrees.
Wherefore, around each of the
outermost exposed corners of the asymmetrical tetrahedra,
we also find three 90-degree
angles which account for four of the cube's eight corners;
while the other four 90-degree
surrounded corners of the cube consist of pairs of 45-degree
corners of the four
asymmetric tetrahedra that were superimposed upon the
central regular tetrahedron to
form the stabilized cube. More complex cubes that will
stand structurally may be
compounded by redundant strutting or tensioning triangles,
but redundancies introduce
microinvisible, high- and low-frequency, self-disintegrative
accelerations, which will
always affect structural enterprises that overlook or
disregard these principles.
|

|
615.05
 In short, structurally stabilized (and otherwise unstable)
cubes are always
and only the most simply compact aggregation of one
symmetrical and four asymmetrical
tetrahedra. Likewise considered, a dodecahedron may
not be a cognizable entity-integrity,
or be rememberable or recognizable as a regenerative
entity, unless it is omnistabilized by
omnitriangulation of its systematic subdivision of all
Universe into either and both
insideness and outsideness, with a small remainder of
Universe to be discretely invested
into the system-entity's structural integrity. No energy
action in Universe would bring
about a blackboard-suggested pentagonal necklace, let
alone 12 pentagons collected edge
to edge to superficially outline a dodecahedron. The
dodecahedron is a demonstrable
entity only when its 12 pentagonal faces are subdivided
into five triangles, each of which is
formed by introducing into each pentagon five struts
radiating unitedly from the
pentagons' centers to their five comer vertexes, of
which vertexes the dodecahedron has
20 in all, to whose number when structurally stabilized
must be added the 12 new
pentagonal center vertexes. This gives the minimally,
nonredundantly structural
dodecahedron 32 vertexes, 60 faces, and 90 strut lines.
In the same way, a structural cube
has 12 triangular vertexes, 8 faces, and 18 linear struts.
In short, structurally stabilized (and otherwise unstable)
cubes are always
and only the most simply compact aggregation of one
symmetrical and four asymmetrical
tetrahedra. Likewise considered, a dodecahedron may
not be a cognizable entity-integrity,
or be rememberable or recognizable as a regenerative
entity, unless it is omnistabilized by
omnitriangulation of its systematic subdivision of all
Universe into either and both
insideness and outsideness, with a small remainder of
Universe to be discretely invested
into the system-entity's structural integrity. No energy
action in Universe would bring
about a blackboard-suggested pentagonal necklace, let
alone 12 pentagons collected edge
to edge to superficially outline a dodecahedron. The
dodecahedron is a demonstrable
entity only when its 12 pentagonal faces are subdivided
into five triangles, each of which is
formed by introducing into each pentagon five struts
radiating unitedly from the
pentagons' centers to their five comer vertexes, of
which vertexes the dodecahedron has
20 in all, to whose number when structurally stabilized
must be added the 12 new
pentagonal center vertexes. This gives the minimally,
nonredundantly structural
dodecahedron 32 vertexes, 60 faces, and 90 strut lines.
In the same way, a structural cube
has 12 triangular vertexes, 8 faces, and 18 linear struts.
|

|
615.06
 The vector equilibrium may not be referred to as a
stabilized structure except
when six struts are inserted as diagonal triangulators
in its six square faces, wherefore the
topological description of the vector equilibrium always
must be 12 vertexes, 20
(triangular) faces, and 30 linear struts, which is also
the topological description of the
icosahedron, which is exactly what the six triangulating
diagonals that have hypotenusal
diagonal vectors longer than the square edge vectors
bring about when their greater force
shrinks them to equilength with the other 24 edge struts.
This interlinkage transforms the
vector equilibrium's complex symmetry of six squares
and eight equiangled triangles into
the simplex symmetry of the icosahedron.
The vector equilibrium may not be referred to as a
stabilized structure except
when six struts are inserted as diagonal triangulators
in its six square faces, wherefore the
topological description of the vector equilibrium always
must be 12 vertexes, 20
(triangular) faces, and 30 linear struts, which is also
the topological description of the
icosahedron, which is exactly what the six triangulating
diagonals that have hypotenusal
diagonal vectors longer than the square edge vectors
bring about when their greater force
shrinks them to equilength with the other 24 edge struts.
This interlinkage transforms the
vector equilibrium's complex symmetry of six squares
and eight equiangled triangles into
the simplex symmetry of the icosahedron.
|

|
615.07
 Both the cube and the vector equilibrium's flexible,
necklacelike, six-square-
face instabilities can be nonredundantly stabilized
as structural integrity systems only by
one or the other of two possible diagonals of each of
their six square faces, which
diagonals are not the same length as the unit vector
length. The alternate diagonaling
brings about positive or negative symmetry of structure.
(See illustration
464.01
and
464.02
in color section.) Thus we have two alternate
cubes or icosahedra, using either the
red diagonal or the blue diagonal. These alternate structural
symmetries constitute typical
positive or negative, non-mirror-imaged intercomplementation
and their systematic,
alternating proclivity, which inherently propagate the
gamut of frequencies uniquely
characterizing the radiated entropy of all the self-regenerative
chemical elements of
Universe, including their inside-out, invisibly negative-Universe-provokable,
split-second-
observable imports of transuranium, non-self-regenerative
chemical elements.
Both the cube and the vector equilibrium's flexible,
necklacelike, six-square-
face instabilities can be nonredundantly stabilized
as structural integrity systems only by
one or the other of two possible diagonals of each of
their six square faces, which
diagonals are not the same length as the unit vector
length. The alternate diagonaling
brings about positive or negative symmetry of structure.
(See illustration
464.01
and
464.02
in color section.) Thus we have two alternate
cubes or icosahedra, using either the
red diagonal or the blue diagonal. These alternate structural
symmetries constitute typical
positive or negative, non-mirror-imaged intercomplementation
and their systematic,
alternating proclivity, which inherently propagate the
gamut of frequencies uniquely
characterizing the radiated entropy of all the self-regenerative
chemical elements of
Universe, including their inside-out, invisibly negative-Universe-provokable,
split-second-
observable imports of transuranium, non-self-regenerative
chemical elements.
|

|
616.00
 Surface Strength of Structures
Surface Strength of Structures
|

|
616.01
 The highest capability in strength of structures exists
in the triangulation of
the system's enclosing structure, due to the greater
action-reaction leverage distance that
opposite sides of the system provide. This is what led
men to hollow out their buildings.
The highest capability in strength of structures exists
in the triangulation of
the system's enclosing structure, due to the greater
action-reaction leverage distance that
opposite sides of the system provide. This is what led
men to hollow out their buildings.
|

|
616.02
 The structural strength of the exterior triangles
is not provided by the "solid"
quality of the exterior shell, but by triangularly interstabilized
lines of force operating
within that shell. They perforate the shell with force
lines. The minimum holes are
triangular.
The structural strength of the exterior triangles
is not provided by the "solid"
quality of the exterior shell, but by triangularly interstabilized
lines of force operating
within that shell. They perforate the shell with force
lines. The minimum holes are
triangular.
|

|
616.03
 The piercing of the shells with triangular holes reduces
the solid or
continuous surface of second-power increase of the shells.
This brings the rate of growth
of structures into something nearer an overall first-power
or linear rate of gain__for the
force lines are only linear. (See also Sec.
412, Closest
Packing of Rods: Surface Tension
Capability, and Sec.
750, Unlimited Frequency of Geodesic
Tensegrities.)
The piercing of the shells with triangular holes reduces
the solid or
continuous surface of second-power increase of the shells.
This brings the rate of growth
of structures into something nearer an overall first-power
or linear rate of gain__for the
force lines are only linear. (See also Sec.
412, Closest
Packing of Rods: Surface Tension
Capability, and Sec.
750, Unlimited Frequency of Geodesic
Tensegrities.)
|

|
617.00
 Cube
Cube
|

|
617.01
 If the cubic form is stable, it has 18 structural
lines. If a dodecahedron is
stable, it has 32 vertexes, 60 faces, and 90 structural
lines. (The primes 5 and, 3 show up
here to produce our icosahedral friend 15.)
If the cubic form is stable, it has 18 structural
lines. If a dodecahedron is
stable, it has 32 vertexes, 60 faces, and 90 structural
lines. (The primes 5 and, 3 show up
here to produce our icosahedral friend 15.)
|

|
617.02
 Whenever we refer to a stable entity, it has to be
structurally valid; therefore,
it has to be triangulated. This does not throw topology
out.
Whenever we refer to a stable entity, it has to be
structurally valid; therefore,
it has to be triangulated. This does not throw topology
out.
|

|
617.03
 A nonstructurally triangulated cube exists only by
self-deceptive topological
accounting: someone shows you a paper or sheet-metal
cube and says, "Here is a
structurally stable cube without any face diagonaling."
And you say, "What do you call
that sheet metal or paper that is occupying the square
faces without which the cube would
not exist? The sheet metal or paper does diagonal the
square but overdoes it redundantly."
A nonstructurally triangulated cube exists only by
self-deceptive topological
accounting: someone shows you a paper or sheet-metal
cube and says, "Here is a
structurally stable cube without any face diagonaling."
And you say, "What do you call
that sheet metal or paper that is occupying the square
faces without which the cube would
not exist? The sheet metal or paper does diagonal the
square but overdoes it redundantly."
|

|
617.04
 A blackboard drawing of a 12-line cube is only an
imaginary, impossible
structure that could not exist in this part of Universe.
It could temporarily hold its shape in
gravity-low regions of space or in another imaginary
Universe. Because we are realistically
interested only in this Universe, we find the cube to
be theoretical only. If it is real, the
linear strut cube has 12 isosceles, right-angle-apexed,
triangular faces.
A blackboard drawing of a 12-line cube is only an
imaginary, impossible
structure that could not exist in this part of Universe.
It could temporarily hold its shape in
gravity-low regions of space or in another imaginary
Universe. Because we are realistically
interested only in this Universe, we find the cube to
be theoretical only. If it is real, the
linear strut cube has 12 isosceles, right-angle-apexed,
triangular faces.
|

|
618.00
 Dimpling Effect
Dimpling Effect
|
 Fig. 618.01 |
618.01
 Definition: When a concentrated load is applied (toward
the center) of any
vertex of any triangulated system, it tends to cause
a dimpling effect. As the frequency or
complexity of successive structures increases, the dimpling
becomes progressively more
localized, and proportionately less force is required
to bring it about.
Definition: When a concentrated load is applied (toward
the center) of any
vertex of any triangulated system, it tends to cause
a dimpling effect. As the frequency or
complexity of successive structures increases, the dimpling
becomes progressively more
localized, and proportionately less force is required
to bring it about.
|

|
618.02
 To illustrate dimpling in various structures, we can
visualize the tetrahedron,
octahedron, and icosahedron made out of flexible steel
rods with rubber joints. Being thin
and flexible, they will bend and yield under pressure.
To illustrate dimpling in various structures, we can
visualize the tetrahedron,
octahedron, and icosahedron made out of flexible steel
rods with rubber joints. Being thin
and flexible, they will bend and yield under pressure.
|

|
618.10
 Tetrahedron: Beginning with the tetrahedron as the
minimum system, it
clearly will require proportionately greater force to
create a "dent." In order to dimple, the
tetrahedron will have to turn itself completely inside
out with no localized effect in
evidence. Thus the dimpling forces a complete change
in the entire structure. The
tetrahedron has the greatest resistance of any structure
to externally applied concentrated
load. It is the only system that can turn itself inside
out. Other systems can have very large
dimples, but they are still local. Even a hemispherical
dimple is still a dimple and still local.
Tetrahedron: Beginning with the tetrahedron as the
minimum system, it
clearly will require proportionately greater force to
create a "dent." In order to dimple, the
tetrahedron will have to turn itself completely inside
out with no localized effect in
evidence. Thus the dimpling forces a complete change
in the entire structure. The
tetrahedron has the greatest resistance of any structure
to externally applied concentrated
load. It is the only system that can turn itself inside
out. Other systems can have very large
dimples, but they are still local. Even a hemispherical
dimple is still a dimple and still local.
|

|
618.20
 Octahedron: If we apply pressure to any one of the
six vertexes of the
octahedron, we will find that one half will fit into
the other half of the octahedron, each
being the shape of a square-based Egyptian pyramid.
It will nest inside itself like a football
being deflated, with one half nested in the other. Although
the octahedron dimples locally,
it reduces its volume considerably in doing so, implying
that it still has a good resistance to
concentrated load.
Octahedron: If we apply pressure to any one of the
six vertexes of the
octahedron, we will find that one half will fit into
the other half of the octahedron, each
being the shape of a square-based Egyptian pyramid.
It will nest inside itself like a football
being deflated, with one half nested in the other. Although
the octahedron dimples locally,
it reduces its volume considerably in doing so, implying
that it still has a good resistance to
concentrated load.
|

|
618.30
 Icosahedron: When we press on a vertex of the icosahedron,
five legs out
of the thirty yield in dimpling locally. There remains
a major part of the space in the
icosahedron that is not pushed in. If we go into higher
and higher triangulation-into
geodesics-the dimpling becomes more local; there will
be a pentagon or hexagon of five
or six vectors that will refuse to yield in tension
and will pop inwardly in compression, and
not necessarily at the point where the pressure is applied.
(See Sec.
905.17.)
Icosahedron: When we press on a vertex of the icosahedron,
five legs out
of the thirty yield in dimpling locally. There remains
a major part of the space in the
icosahedron that is not pushed in. If we go into higher
and higher triangulation-into
geodesics-the dimpling becomes more local; there will
be a pentagon or hexagon of five
or six vectors that will refuse to yield in tension
and will pop inwardly in compression, and
not necessarily at the point where the pressure is applied.
(See Sec.
905.17.)
|
| Next Section: 620.00 |