986.520 Einstein's Equation
986.521 Remembering that in any given dimensional system of reference the vector's length represents a given mass multiplied by a given velocity, we have in the present instance the physical evidence that the surface area of the T Quanta Module tetrahedron exactly equals the area of the edge length__0.9995__"squared." In this case of the T Quanta Module the edge length of 0.9995 of the foldable square (the visibly undetectable) is 0.0005 less than the length of the prime vector of 1.000.
986.522 The generalized isotropic vector matrix's prime vector to the second power__"squared"__becomes physically visible in the folded-square T tetra modules. (Try making one of them yourself.) This visible "squaring" of the surface area of the exactly one-energy-quantum module tetrahedron corresponds geometrically to what is symbolically called for in Einstein's equation, which language physics uses as a nonengineering-language symbolism (as with conventional mathematics), and which does not preintermultiply mass and velocity to produce a vector of given length and angular direction-ergo, does not employ the integrated vectorial component VE__ergo, must express V2 in separate components as M (mass) times the velocity of energy unfettered in vacuo to the second power, c2. However, we can say Mc2 = V2, the engineering expression V2 being more economical. When T = the T Quanta Module, and when the T Quanta Module = one energy quantum module, we can say:
one module = 0.99952
986.523 In the Einstein equation the velocity__lower-case c__of all radiation taken to the second power is omnidirectional-ergo, its quasispheric surface-growth rate is at the second power of its radial-linear-arithmetic growth rate__ergo, c2. (Compare Secs. 1052.21 and 1052.30.) Thus Einstein's equation reads E = Mc2, where E is the basic one quantum or one photon energy component of Universe.
986.524 With all the foregoing holding true and being physically demonstrable, we find the vector minus 0.0005 of its full length producing an exactly square area that folds into a tetrahedron of exactly one quantum module, but, we must remember, with a unit- integral-square-surface area whose edge length is 0.0005 less than the true V2 vector, i.e., less than Mc2. But don't get discouraged; as with the French Vive la Diff‚rence, we find that difference of 0.0005 to be of the greatest possible significance . . . as we shall immediately learn.
986.540 Volume-surface Ratios of E Quanta Module and Other Modules
986.541 Now, reviewing and consolidating our physically exploratory gains, we note that in addition to the 0.9995 V2-edged "square"-surfaced T Quanta Module tetrahedron of exactly the same volume as the A, B, C, or D Quanta Modules, we also have the E Quanta Module__or the "Einstein Module" __whose square edge is exactly vector V = 1.0000 (alpha), but whose volume is 1.001551606 when the A Quanta Module's volume is exactly 1.0000 (alpha), which volume we have also learned is uncontainable by chemical structuring, bonding, and the mass-attraction law.
986.542 When the prime-unit vector constitutes the radial distance outward from the triacontahedron's volumetric center O to the mid-points C of each of its mid-diamond faces, the volume of the rhombic triacontahedron is then slightly greater than tetravolume 5, being actually tetravolume 5.007758031. Each of the rhombic triacontahedron's 120 internally structured tetrahedra is called an E Quanta Module, the "E" for Einstein, being the transformation threshold between energy convergently self-interfering as matter = M, and energy divergently dispersed as radiation = c2. Let us consider two rhombic triacontahedra: (1) one of radius 0.9995 V of exact tetravolume 5; and (2) one of radius 1.0000 (alpha) of tetravolume 5.007758031. The exact prime-vector radius 1.0000 (alpha) rhombic triacontahedron volume is 0.007758031 (1/129th) greater than the tetravolume 5__i.e., tetravolume 5.007758031. This means that each E Quanta Module is 1.001551606 when the A Quanta Module is 1.0000.
986.543 The 0.000517 radius difference between the 0.999483-radiused rhombic triacontahedron of exactly tetravolume 5 and its exquisitely minute greater radius-1.0000 (alpha) prime vector, is the exquisite difference between a local-in-Universe energy-containing module and that same energy being released to become energy radiant. Each of the 120 right-angle-cornered T Quanta Modules embraced by the tetravolume-5 rhombic triacontahedron is volumetrically identical to the A and B Quanta Modules, of which the A Modules hold their energy and the B Modules release their energy (Sec. 920). Each quanta module volume is 0.04166__i.e., 1/24 of one regular primitive tetrahedron, the latter we recall being the minimum symmetric structural system of Universe. To avoid decimal fractions that are not conceptually simple, we multiply all the primitive hierarchy of symmetric, concentric, polyhedral volumes by 24__after which we can discuss and consider energetic-synergetic geometry in always-whole-rational-integer terms.
986.544 We have not forgotten that radius I is only half of the prime-unit vector of the isotropic vector matrix, which equals unity 2 (Sec. 986.160). Nor have we forgotten that every square is two triangles (Sec. 420.08); nor that the second-powering of integers is most economically readable as "triangling"; nor that nature always employs the most economical alternatives__but we know that it is momentarily too distracting to bring in these adjustments of the Einstein formula at this point.
986.545 To discover the significance of the "difference" all we have to do is make another square with edge length of exactly 1.000 (alpha) (a difference completely invisible at our one-foot-to-the-edge modeling scale), and now our tetrahedron folded out of the model is an exact geometrical model of Einstein's E = Mc2, which, expressed in vectorial engineering terms, reads E = V2 ; however, its volume is now 0.000060953 greater than that of one exact energy quanta module. We call this tetrahedron model folded from one square whose four edge lengths are each exactly one vector long the E Module, naming it for Einstein. It is an exact vector model of his equation.
986.546 The volumetric difference between the T Module and the E Module is the difference between energy-as-matter and energy-as-radiation. The linear growth of 0.0005 transforms the basic energy-conserving quanta module (the physicists' particle) from matter into one minimum-limit "photon" of radiant energy as light or any other radiation (the physicists' wave).
986.547 Einstein's equation was conceived and calculated by him to identify the energy characteristics derived from physical experiment, which defined the minimum radiation unit__the photon__E = Mc2. The relative linear difference of 0.000518 multiplied by the atoms' electrons' nucleus-orbiting diameter of one angstrom (a unit on only l/40-millionth of an inch) is the difference between it is matter or it is radiation.... Vastly enlarged, it is the same kind of difference existing between a soap bubble existing and no longer existing__"bursting," we call it__because it reached the critical limit of spontaneously coexistent, cohesive energy as-atoms-arrayed-in-liquid molecules and of atoms rearranged in dispersive behavior as gases. This is the generalized critical threshold between it is and it isn't.... It is the same volume-to-tensional-surface-enclosing-capability condition displayed by the soap bubble, with its volume increasing at a velocity of the third power while its surface increases only as velocity to the second power. Its tension- embracement of molecules and their atoms gets thinned out to a one-molecule layer, after which the atoms, behaving according to Newton's mass-interattraction law, become circumferentially parted, with their interattractiveness decreasing acceleratingly at a second-power rate of the progressive arithmetical distance apart attained__an increase that suddenly attains critical demass point, and there is no longer a bubble. The same principle obtains in respect to the T Quanta Module E Quanta Module__i.e., matter transforming into radiation.
986.548 The difference between the edge length of the square from which we fold the E Quanta Module and the edge length of the square from which we fold the T Quanta Module is exquisitely minute: it is the difference between the inside surface and the outside surface of the material employed to fabricate the model. In a 20-inch-square model employing aluminum foil

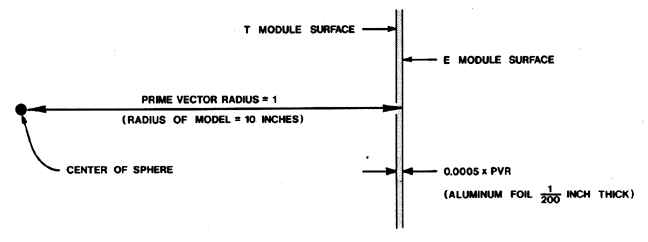
1/200th of an inch thick, the E Module would be congruent with the outside surface and the T Module would be congruent with the inside surface, and the ratio of the edge lengths of the two squares is as 1 is to 0.0005, or 0.0005 of prime vector radius of our spherical transformation. This minuscule modelable difference is the difference between it is and it isn't__which is to say that the dimensional difference between matter and radiation is probably the most minute of all nature's dimensioning: it is the difference between inside-out and outside-out of positive and negative Universe.
986.549 Because we have obtained an intimate glimpse of matter becoming radiation, or vice versa, as caused by a minimum-structural-system tetrahedron's edge-length growth of only 129 quadrillionths of an inch, and because we have been paying faithful attention to the most minute fractions of difference, we have been introduced to a whole new frontier of synergetics exploration. We have discovered the conceptual means by which the 99 percent of humanity who do not understand science may become much more intimate with nature's energetic behaviors, transformations, capabilities, and structural and de-structural strategies.
986.550 Table: Relative Surface Areas Embracing the Hierarchy of Energetic Quanta Modules: Volumes are unit. All Module Volumes are 1, except the radiant E Module, whose Surface Area is experimentally evidenced Unity:
ENERGY PACKAGE / SURFACE AREA
V = Vector (linear)
V = Mass × velocity = Energy Package
V2 = Energy package's surface

1 Unit vector of isotropic vector matrix

Vector × Vector = Surface (Energy as local energy system-containment capability)
= Outer array of energy packages.6

Mass = F = Relative frequency of primitive-system-subdivision energy-event occupation.
"SURFACE"
AREA		 VOLUME
A Quanta Module 0.9957819158 1 HOLD
T Quanta Module 0.9989669317 1 ENERGY
"Einstein" E Module 1.0000000000 1.00155
B Quanta Module 1.207106781
C Quanta Module 1.530556591
D Quanta Module 1.896581995
A' Module 2.280238966
B' Module 2.672519302 1 RELEASE
C' Module 3.069597104 1 ENERGY
D' Module 3.469603759
A" Module 3.871525253 1
B" Module 4.27476567 1
C" Module 4.678952488 1
D" Module 5.083841106 1
(For a discussion of C and D Modules see Sec. 986.413.)

(Footnote 6: The VE surface displays the number of closest-packed spheres of the outer layer. That surface = f2; ergo, the number of energy-package spheres in outer layer shell = surface, there being no continuum or solids.)
986.560 Surprise Nestability of Minimod T into Maximod T

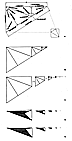Fig. 986.561 		986.561 The 6 + 10 + 15 = 31 great circles of icosahedral symmetries (Fig. 901.03) produce the spherical-surface right triangle AC''B; CAB is subdivisible into four spherical right triangles CDA, CDE, DFE, and EFB. Since there are 120 CAB triangles, there are 480 subdivision-right-surface triangles. Among these subdivision-right triangles there are two back-to-back 90-degree surface angles at D__CDA and CDE__and two back-to-back degree surface angles at F__CFE and EFB. The surface chord DE of the central angle DOE is identical in magnitude to the surface chord EB of the central angle EOB, both being 13.28 degrees of circular azimuth. Surface chord FB of central angle FOB and surface chord AD of central angle AOD are identical in magnitude, both being 10.8 degrees azimuth. In the same manner we find that surface chord EF of central angle EOF constitutes the mutual edge of the two surface right triangles CFE and BFE, the central- angle magnitude of EOF being 7.77 degrees azimuth. Likewise, the central angles COA and COF of the surface chords CA and CF are of the same magnitude, 20.9 degrees. All the above data suggest a surprising possibility: that the small corner triangle AC"B itself can be folded on its three internal chord lines CD, CE, and EF, while joining its two edges AC and CF, which are of equal magnitude, having central angles of 20.9 degrees. This folding and joining of F to A and of B to D cancels out the congruent-letter identities F and D to produce the tetrahedron ABEC. (See Fig. 986.561.)
986.562 We find to our surprise that this little flange-foldable tetrahedron is an identically angled miniature of the T Quanta Module OABCt and that it can fit elegantly into the identically angled space terminating at O within the inner reaches of vacant OABC, with the miniature tetrahedron's corner C becoming congruent with the system's center O. The volume of the Minimod T is approximately 1/18 that of the Maximod T Quanta Module or of the A or B Modules.
986.570 Range of Modular Orientations
986.571 Now we return to Consideration 13 of this discussion and its discovery of the surface-to-central-angle interexchanging wave succession manifest in the cosmic hierarchy of ever-more-complex, primary structured polyhedra__an interchanging of inside-out characteristics that inherently produces positive-negative world conditions; ergo, it propagates__inside-to-outside-to-in__pulsed frequencies. With this kind of self- propagative regenerative function in view, we now consider exploring some of the implications of the fact that the triangle C'AB is foldable into the E Quanta Module and is also nestable into the T Quanta Module, which produces many possibilities:
  1. The triangle AC'B will disconnect and reverse its faces and complete the enclosure of the T Quanta Module tetrahedron.
  2. The 120 T Quanta Modules, by additional tension-induced twist, take the AC"B triangles AB ends end-for-end to produce the additional radius outwardly from O to convert the T Quanta Modules into "Einstein" E Quanta Modules, thus radiantly exporting all 120 modules as photons of light or other radiation.
  3. The triangle AC"B might disconnect altogether, fold itself into the miniature T Quanta Module, and plunge inwardly to fill its angularly matching central tetrahedral vacancy.
  4. The outer triangle may just stay mishinged and flapping, to leave the tetrahedron's outer end open.
  5. The outer triangle might come loose, fold itself into a miniature T Quanta Module, and leave the system.
  6. The 120 miniature T Quanta Modules might fly away independently__as, for instance, cosmic rays, i.e., as minimum modular fractions of primitive systems.
  7. All 120 of these escaping miniature T Quanta Modules could reassemble themselves into a miniature 1/120 triacontahedron, each of whose miniature T Module's outer faces could fold into mini-mini T Modules and plunge inwardly in ever-more-concentrating demonstration of implosion, ad infinitum.

There are 229,920 other possibilities that any one of any other number of the 120 individual T Module tetrahedra could behave in any of the foregoing seven alternate ways in that vast variety of combinations and frequencies. At this borderline of ultrahigh frequency of intertransformability between matter and electromagnetic radiation we gain comprehension of how stars and fleas may be designed and be born.
986.580 Consideration 15: Surface Constancy and Mass Discrepancy
986.581 Those AC"B triangles appear in the upper left-hand corner of either the T Module's or the E Module's square areas COC'C", one of which has the edge length 0.994 V and the other the edge length of 1.0000 (alpha) V. Regardless of what those AC"B triangles may or may not do, their AC"B areas, together with the areas of the triangles ACO, ABO, and BCO, exactly constitute the total surface area of either the T Module or the E Module.

Surface of T Module =.994 V2

Surface of E Module = 1.00000 (alpha) V2
986.582 The outer triangle AC"B of the T Quanta Module is an inherent energy conserver because of its foldability into one (minimum-something) tetrahedron. When it folds itself into a miniature T Module with the other 119 T Modules as a surface-closed rhombic triacontahedron, the latter will be a powerful energy conserver__perhaps reminiscent of the giant-to-dwarf-Star behavior. The miniature T Module behavior is also similar to behaviors of the electron's self-conservation. This self-conserving and self- contracting property of the T Quanta Modules, whose volume energy (ergo, energy quantum) is identical to that of the A and B Modules, provides speculative consideration as to why and how electron mass happens to be only 1/1836 the mass of the proton.
986.583 Certain it is that the T Quanta Module E Quanta Module threshold transformation makes it clear how energy goes from matter to radiation, and it may be that our little corner triangle AC"B is telling us how radiation retransforms into matter.
986.584 The volume of the T Quanta Module is identical with the volumes of the A and B Quanta Modules, which latter we have been able to identify with the quarks because of their clustering in the cosmically minimum, allspace-filling three-module Mites as A +, A -, and B, with both A's holding their energy charges and B discharging its energy in exact correspondence with the quark grouping and energy-holding-and-releasing properties, with the A Modules' energy-holding capabilities being based on their foldability from only one triangle, within which triangle the reflection patterning guarantees the energy conserving. (See Secs. 921 and 986.414)
986.585 As we study the hierarchy of the surface areas of constant volume 1 and their respective shapes, we start with the least-surface A Quanta Module which is folded out of one whole triangle, and we find that no other triangle is enclosed by one triangle except at the top of the hierarchy, where in the upper left-hand corner we find our Minimod T or Minimod E tetrahedron foldable out of our little triangle AC"B, whose fold-line patterning is similar to that of the triangle from which the A Quanta Module is folded. In between the whole foldable triangular blank of the A Quanta Module and the whole foldable triangular blank of the Minimod T or Minimod E, we have a series of only asymmetrical folding blanks-until we come to the beautiful squares of the T and E Quanta Modules, which occur just before we come to the triangles of the minimod tetrahedra, which suggests that we go from radiation to matter with the foldable triangle and from matter to radiation when we get to the squares (which are, of course, two triangles).
Next Section: 986.600
Copyright © 1997 Estate of R. Buckminster Fuller