Interactions of Symmetries: Secondary Great-circle
Sets
|
|
987.400
Interactions of Symmetries: Secondary Great-circle
Sets
|
|
|
987.410
Icosa Phase of Rationality
|
|
|
987.411
The 96 secondary great circles of the VE divide the
chorded edge of the VE
(which is the unit vector radius of synergetics) into
rational linear fractions of the edge
length__i.e., 1/2, 3/10, 1/4, 1/6, 1/10__and these fractions
embrace all the intercombinings
of the first four prime numbers 1, 2, 3, and 5.
|
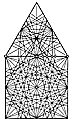 Fig. 987.412 |
987.412
For an illustration of how the four VE great circles
of 60-degree central
angles subdivide the central-angle chord increments,
see Fig.
987.412.
|
|
|
987.413
Next recalling the jitterbug transformation of the
VE into the icosa with its
inherent incommensurability brought about by the
2:sqrt(2) = sqrt(2):1
transformation ratio, and recognizing that the transformation
was experimentally
demonstrable by the constantly symmetrical contracting
jitterbugging, we proceed to
fractionate the icosahedron by the successive l5 great
circles, six great circles (icosa type),
and 10 great circles whose self-fractionation produces
the S Modules8 as well as the T and
E Modules.
(Footnote 8: See Sec. 988.) |
|
|
987.414
But it must be recalled that the experimentally demonstrable
jitterbug model
of transformation from VE to icosa can be accomplished
through either a clockwise or
counterclockwise twisting, which brings about 30 similar
but positive and 30 negative
omniintertriangulated vector edge results.
|
|
|
987.415
The midpoints of each of these two sets of 30 vertexes
in turn provide the
two alternate sets of 30 poles for the spin-halving
of the 15 great circles of Symmetry #6,
whose spinning in turn generates the 120 right spherical
triangles (60 positive, 60
negative) of the icosahedral system.
|
|
|
987.416
The 120 right triangles, evenly grouped into 30 spherical
diamonds, are
transformed into 30 planar diamonds of central angles
identical to those of the 30 spherical
diamonds of the 15 great circles of the icosa. When
the radius to the center of the face of
the rhombic triacontahedron equals 0.9994833324....
of the unit vector radius of
Synergetics (1.000), the rhombic triacontahedron has
a tetravolume of 5 and each of its
120 T Quanta Modules has a volume of one A Module. When
the radius equals 1, the
volume of the rhombic triacontahedron is slightly larger
(5.007758029), and the
corresponding E Module has a volume of 1.001551606 of
the A Module. (See Sec.
986.540)
|
988.00
Icosahedron and Octahedron: S Quanta Module
|
|
988.100
Octa-icosa Matrix
|
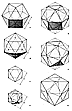 Fig. 988.00  Fig. 988.100 |
988.110
The icosahedron positioned in the octahedron describes
the S Quanta
Modules. (See Fig.
988.100.) Other references to the
S Quanta Modules may be found at
Secs.
100.105,
100.322, Table
987.121, and
987.413.
|
|
|
988.111
As skewed off the octa-icosa matrix, they are the volumetric
counterpart of
the A and B Quanta Modules as manifest in the nonnucleated
icosahedron. They also
correspond to the 1/120th tetrahedron of which the triacontahedron
is composed. For
their foldable angles and edge-length ratios see Figs.
988.111A-B.
|
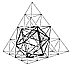 Fig. 988.12 |
988.12
The icosahedron inscribed within the octahedron is
shown at Fig.
988.12.
|
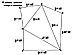 Fig. 988.13A 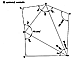 Fig. 988.13B 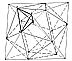 Fig. 988.13C |
988.13
The edge lengths of the S Quanta Module are shown
at Fig.
988.13A.
|
|
|
988.14
The angles and foldability of the S Quanta Module
are shown at Fig. 988.13B.
|
|
|
988.20
Table: Volume-area Ratios of Modules and Polyhedra
of the Primitive
Hierarchy:
* Volume and area of A Module considered as unity. ** Icosahedron inside octahedron. |
990.00
Triangular and Tetrahedral Accounting
 Fig. 990.01 |
990.01
All scientists as yet say "X squared," when they encounter
the expression
"X2," and "X cubed," when they encounter "X3" But the
number of squares enclosed by
equimodule-edged subdivisions of large gridded squares
is the same as the number of
triangles enclosed by equimodule-edged subdivisions
of large gridded triangles. This
remains true regardless of the grid frequency, except
that the triangular grids take up less
space. Thus we may say "triangling" instead of "squaring"
and arrive at identical
arithmetic results, but with more economical geometrical
and spatial results. (See Illus.
990.01 and also
415.23.)
|
|
|
990.02
Corresponding large, symmetrical agglomerations of
cubes or tetrahedra of
equimodular subdivisions of their edges or faces demonstrate
the same rate of third-power
progression in their symmetrical growth (1, 8, 27, 64,
etc.). This is also true when divided
into small tetrahedral components for each large tetrahedron
or in terms of small cubical
components of each large cube. So we may also say "tetrahedroning"
instead of "cubing"
with the same arithmetical but more economical geometrical
and spatial results.
|
|
|
990.03
We may now say "one to the second power equals one,"
and identify that
arithmetic with the triangle as the geometrical unit.
Two to the second power equals four:
four triangles. And nine triangles and 16 triangles,
and so forth. Nature needs only
triangles to identify arithmetical "powering" for the
self-multiplication of numbers. Every
square consists of two triangles. Therefore, "triangling"
is twice as efficient as "squaring."
This is what nature does because the triangle is the
only structure. If we wish to learn how
nature always operates in the most economical ways,
we must give up "squaring" and
learn to say "triangling," or use the more generalized
"powering."
|
|
|
990.04
There is another very trustworthy characteristic of
synergetic accounting. If
we prospectively look at any quadrilateral figure that
does not have equal edges, and if we
bisect and interconnect those mid-edges, we always produce
four dissimilar quadrangles.
But when we bisect and interconnect the mid-edges of
any arbitrary triangle__equilateral,
isosceles, or scalene__four smaller similar and equisized
triangles will always result. There
is no way we can either bisect or uniformly subdivide
and then interconnect all the edge
division points of any symmetrical or asymmetrical triangle
and not come out with omni-
identical triangular subdivisions. There is no way we
can uniformly subdivide and
interconnect the edge division points of any asymmetrical
quadrangle (or any other
different-edge-length polygons) and produce omnisimilar
polygonal subdivisions.
Triangling is not only more economical; it is always
reliable. These characteristics are not
available in quadrangular or orthogonal accounting.
|
|
|
990.05
The increasingly vast, comprehensive, and rational
order of arithmetical,
geometrical, and vectorial coordination that we recognize
as synergetics can reduce the
dichotomy, the chasm between the sciences and the humanities,
which occurred in the
mid-nineteenth century when science gave up models because
the generalized case of
exclusively three-dimensional models did not seem to
accommodate the scientists' energy-
experiment discoveries. Now we suddenly find elegant
field modelability and conceptuality
returning. We have learned that all local systems are
conceptual. Because science had a
fixation on the "square," the "cube," and the 90-degree
angle as the exclusive forms of
"unity," most of its constants are irrational. This
is only because they entered nature's
structural system by the wrong portal. If we use the
cube as volumetric unity, the
tetrahedron and octahedron have irrational number volumes.
|
995.00
Vector Models of Magic Numbers
|
|
995.01
Magic Numbers
|
|
|
995.02
The magic numbers are the high abundance points in
the atomic-isotope
occurrences. They are 2, 8, 20, 50, 82, 126, ...,
! For every nonpolar vertex, there are
three vector edges in every triangulated structural
system. The Magic Numbers are the
nonpolar vertexes. (See Illus.
995.31.)
|
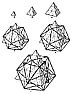 Fig. 995.03 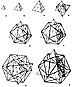 Fig. 995.03A |
995.03
In the structure of atomic nuclei, the Magic Numbers
of neutrons and
protons correspond to the states of increased stability.
Synergetics provides a symmetrical,
vector-model system to account for the Magic Numbers
based on combinations of the
three omnitriangulated structures: tetrahedron, octahedron,
and icosahedron. In this model
system, all the vectors have the value of one-third.
The Magic Numbers of the atomic
nuclei are accounted for by summing up the total number
of external and internal vectors
in each set of successive frequency models, then dividing
the total by three, there being
three vectors in Universe for every nonpolar vertex.
|
|
|
995.10
Sequence
|
|
|
995.11A
The sequence is as follows:
|
|
|
995.11
The sequence is as follows:
|
|
|
995.12
Magic Number 28: The Magic Number 28, which introduces
the cube and
the octahedron to the series, was inadvertently omitted
from Synergetics 1. The three-
frequency tetrahedron is surrounded by an enlarged two-frequency
tetrahedron that shows
as an outside frame. This is a negative tetrahedron
shown in its halo aspect because it is
the last case to have no nucleus. The positive and negative
tetrahedra combine to provide
the eight corner points for the triangulated cube. The
outside frame also provides for an
octahedron in the middle. (See revised Figs.
995.03A
and
995.31A.)
|
|
|
995.20
Counting
|
|
|
995.21
In the illustration, the tetrahedra are shown as opaque.
Nevertheless, all the
internal vectors defined by the isotropic vector matrix
are counted in addition to the
vectors visible on the external faces of the tetrahedra.
|
|
|
995.30
Reverse Peaks in Descending Isotope Curve
|
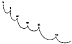 Fig. 995.31  Fig. 995.31A |
995.31
There emerges an impressive pattern of regularly positioned
behaviors of the
relative abundances of isotopes of all the known atoms
of the known Universe. Looking
like a picture of a mountainside ski run in which there
are a series of ski-jump upturns of
the run, there is a series of sharp upward-pointing
peaks in the overall descent of this
relative abundance of isotopes curve, which originates
at its highest abundance in the
lowest-atomic-numbered elemental isotopes.
|
|
|
995.32
The Magic Number peaks are approximately congruent
with the atoms of
highest structural stability. Since the lowest order
of number of isotopes are the most
abundant, the inventory reveals a reverse peak in the
otherwise descending curve of
relative abundance.
|
|
|
995.33
The vectorial modeling of synergetics demonstrates
nuclear physics with
lucid comprehension and insight into what had been heretofore
only instrumentally
apprehended phenomena. In the post-fission decades of
the atomic-nucleus explorations,
with the giant atom smashers and the ever more powerful
instrumental differentiation and
quantation of stellar physics by astrophysicists, the
confirming evidence accumulates.
|
|
|
995.34
Dr. Linus Pauling has found and published his spheroid
clusters designed to
accommodate the Magic Number series in a logical system.
We find him__although
without powerful synergetic tools__in the vicinity of
the answer. But we can now identify
these numbers in an absolute synergetic hierarchy, which
must transcend any derogatory
suggestion of pure coincidence alone, for the coincidence
occurs with mathematical
regularity, symmetry, and a structural logic that identifies
it elegantly as the model for the
Magic Numbers.
|
| Next Chapter: 1000.00 |