100.01
Introduction: Scenario of the Child
[100.01-100.63 Child as Explorer Scenario]
|
100.010
Awareness of the Child: The simplest descriptions
are those expressed by
only one word. The one word alone that describes the
experience "life" is "awareness."
Awareness requires an otherness of which the observer
can be aware. The communication
of awareness is both subjective and objective, from
passive to active, from otherness to
self, from self to otherness.
|
|
|
100.011
Awareness is the otherness saying to the observer,
"See Me." Awareness is
the observer saying to self, "I see the otherness."
Otherness induces awareness of self.
Awareness is always otherness inductive. The total complex
of otherness is the
environment.
|
|
|
|
|
|
(Compare Secs. 264.10 and 1073.12.) |
|
|
100.013
Life begins only with otherness. Life begins with
awareness of environment.
In Percival W. Bridgman's identification of Einstein's
science as operational science, the
comprehensive inventory of environmental conditions
is as essential to "experimental
evidence" as is the inventory of locally-focused-upon
experimental items and
interoperational events.
|
|
|
100.014
The child's awareness of otherness phenomena can be
apprehended only
through its nerve-circuited sense systems and through
instrumentally augmented, macro-
micro, sense-system extensions__such as eyeglasses. Sight
requires light, however, and
light derives only from radiation of celestial entropy,
where Sunlight is starlight and fossil
fuels and fire-producing wood logs are celestial radiation
accumulators; ergo, all the
sensings are imposed by cosmic environment eventings.
|
|
|
100.015
The child apprehends only sensorially. The combined
complex of different
sensorial apprehendings (touch, smell, hear, see) of
each special case experience are
altogether coordinated in the child's brain to constitute
"awareness" conceptions. The
senses can apprehend only other-than-self "somethings"__for
example, the child's left
hand discovering its right hand, its toe, or its mother's
finger. Brains differentially
correlate the succession of special case informations
communicated to the brain by the
plurality of senses. The brain distinguishes the new,
first-time-event, special case
experiences only by comparing them with the set of all
its recalled prior cognitions.
|
|
|
100.016
Although children have the most superb imaginative
faculties, when they
explore and arrive at new objective formulations, they
rely__spontaneously and
strategically__only upon their own memory of relevant
experiences. With anticipatory
imagination children consider the consequences of their
experiments, such as a physical
experiment entailing pure, unprecedented risk yet affording
a reasonable possibility of
success and including a preconception of the probable
alternative physical consequences of
their attempt. For example, they may conceivably jump
over a ditch today even though it
is wider than any over which they have previously leapt.
They only make the attempt
because they have also learned experientially that,
as they grow older and bigger, they are
often surprised to find that they can jump farther and
higher than ever before. "How do all
my muscles feel about it now?" and "Shall I or shall
I not try?" become exquisitely
aesthetic questions leading to synergetically integrated,
physical-metaphysical, split-second
self-appraisals and exclusively intuitive decisions.
If it's "Everything go!" all thoughts of
negative consequences are brushed aside.
|
|
|
100.017
Children conduct their spontaneous explorations and
experiments with naive
perceptivity. They have an innate urge first subjectively
to sort out, find order in,
integratively comprehend, and synergetically memory-bank
their experience harvests as
intertransformability system sets. Thereafter they eagerly
seek to demonstrate and
redemonstrate these sets as manifest of their comprehension
and mastery of the synergetic
realizability of the system's physical principles. Consequently
children are the only
rigorously pure physical scientists. They accept only
sensorially apprehensible,
experimentally redemonstrable physical evidence.
|
|
|
100.018
Things = events = patterns = somersaults = intertransformability
systems ...
that's what delights a girl as she accepts her uncle's
invitation to face him, take hold of his
two hands, walk up his front until, falling backward__and
still holding his hands__the child
finds herself looping the loop, heels over head, to
land with feet on the ground and head
high.... "Wow, let's do it again!"
|
|
|
100.020
Human Sense Awareness
|
|
|
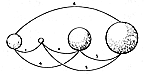
ULTRAVIOLET THRESHOLD (Only macro-instrument-apprehensible) (See Secs. 267.02, 801.01-24, and 1053.85.) |
|
|
100.021
The direct sensing of information may sometimes be
deceptive and illusory
due to such factors as coincidence, congruence, or the
time-and-angle distortions of
perspective. For instance, the parallel railroad tracks
seem (mistakenly) to converge at the
horizon, and the apparently "motionless" remote stars
seem (mistakenly) fixed, while they
are in fact speeding at celestial macrorates.
|
|
|
100.022
Children can learn from their successive observations
of the rotational
progression of angles that the hour and minute hands
of a clock have moved; that the tree
and the vine have grown; and that the pond's top has
frozen into ice that surprisingly
floats__getting colder usually means getting denser and
heavier per given volume, which
erroneously suggests that ice should sink to the pond's
bottom. But the crystallization of
water forms a "space frame" whose members do not fill
allspace. This vacated space
embraces and incorporates oxygen from the atmosphere__which
makes ice lighter than
water. The crystallization of water takes up more room
than does the water in its liquid
nonform condition. Crystallization is structurally and
vectorially linear: it is not allspace-
filling. Crystalline structurings are interspersed by
additional atmospheric molecules
occupying more volume (ergo, having less mass); the
process of crystallization cracks
open its closed containers. If ice did not float, if
ice sank to the bottom, life would have
long since disappeared from planet Earth.
|
|
|
100.023
Comprehensively concerned children can learn how to
avoid the miscarriages
of misconceptioning as induced by too-brief reviews
of their progressive experiences as
observed from too few viewpoints or loci. They can learn__as
did Einstein__of the
plurality of different, instrumentally measured, time-angle-and-size
aspects of the same
phenomena as viewed from different given environmental
surrounding points by different
observers at as close to the "same" time as possible,
taken at "almost the same time" as
well as at distinctly different times. The foregoing
is what led Einstein to the discovery of
relativity.
|
|
|
100.030
Resolvability Limits
|
Fig. 100.031 |
100.031
The visual limits of "now-you-see-it-now-you-don't,"
yes-no-yes-no,
something-nothing-something-nothing, dot-dash-dot-dash
are relative size-scale
discernibilities spoken of technically as resolution.
These resolvability limits of the human
eye may be pictured as (in Fig. 100.031)(follows:)
The finest "smooth"-surface, intercolor-crossblending,
continuum photogravure printing is
accomplished with a benday screen that uses 200 unique
color dots per square inch of
printed surface. (See Secs. 260.11
and 260.22.)
|
|
|
100.032
A point-to-able something may be much too small to
be optically resolved
into its constituent polyhedral characteristics, yet
be unitarily differentiated as a black
speck against a white background. Because a speck existed
yet defied their discernment of
any feature, mathematicians of the premicroscope era
mistakenly assumed a speck to be
self-evidently unitary, indivisible, and geometrically
employable as a nondimensional
"point." (See Secs. 262.02-05,
264,
527.25, and
530.11.)
|
|
|
100.033
A plurality of points became the "building blocks"
with which the
mathematicians of the day before microscopes imaginatively
constructed their lines.
"Lines" became the one-dimensional, substanceless "logs"
that they floored together in
their two-dimensional, planar, thicklessness "rafts."
Finally they stacked these planar rafts
one upon another to build a "solid" three-dimensional
"cube," but having none of the
essential characteristics of four-dimensional reality__i.e.,
having neither temperature,
weight, nor longevity.
|
|
|
100.10
Subdivision of Tetrahedral Unity
|
|
|
100.101
Synergetic Unity: Quantum mechanics commences with
the totality of
energy of physical Universe__energy intertransformable
either as matter or as radiation.
Quantum mechanics assumes conservation. Energy can be
neither created nor lost. Cosmic
energy is plural unity, always-and-only coexistent,
complementarily complex unity, i.e.,
synergetic unity, consisting of an overlapping mix of
infrequent big events and frequent
little ones. Multiplication of energy events can be
accomplished only by progressive
subdividing of its cosmic unity.
|
|
|
100.102
The child-scientist's show opens with reiteration of
rigorous science's one-
and-only acceptable proof: experientially redemonstrable
physical evidence. All of the
scenario's proofs__and their rationally interrelated
number values__derive exclusively
from progressive equatorial-symmetry-halvings of Universe's
minimum structural system:
the tetrahedron. Multiplication occurs only through
progressive fractionation of the
original complex unity of the minimum structural system
of Universe: the tetrahedron.
|
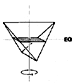 Fig. 100.103 |
100.103
Rational numerical and geometrical values derive from
(a) parallel and (b)
perpendicular halving of the tetrahedron.
(See Fig. 100.103.)
|
|
|
100.104
The three-way, symmetry-imposed, perpendicular bisecting
of each of the
tetrahedron's four triangular faces results in an inadvertent
thirding. This halving and
inadvertent thirding physically isolate the prime number
three and its multiples and
introduce the 24 A Quanta Modules.
(See Sec. 911,
Fig. 913.01 , and
Table 943.)
|
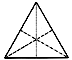 Fig. 100.1041 |
100.1041
The initial halvings of the triangular facets inadvertently
accomplish both
thirdings and quintasectings. Halving a triangle by
perpendicular bisectors finds three ways
of doing so. (See Fig. 100.1041.)
|
|
|
100.1042
Great circles inherently halve unity. The six positive
and six negative great
circles spin around the 12 positive and 12 negative
poles vertexially identified by the 12-
great-circle and four-great-circle intersections of
the vector equilibrium producing the
pentagons from the quintasectings.
|
|
|
100.105
All the geometries in the cosmic hierarchy
(see Table 982.62)
emerge from
the successive subdividing of the tetrahedron and its
combined parts. After the initial
halvings and inadvertent thirdings inherent in the bisecting
of the triangles as altogether
generated by all seven sets of the great circle equators
of symmetrical-systems spin
(Sec. 1040),
we witness the emergence of:
|
 Fig. 100.120 |
100.120
Icosa and Tetra: The icosahedron concentric within,
but flushly askew, in
the four-frequency truncated tetrahedron completes the
whole cosmic hierarchy as
subdivisioning of the primitive unity of the tetrahedron__one
quantum__the minimum
structural system of Universe. Looked at perpendicularly
to the middle of any of the
tetrahedron's four truncated faces__as a line of sight__the
icosahedron appears at the
center of volume of the tetrahedron as a four-dimensional
symmetrical structure. (See Fig. 100.120)
|
|
|
100.20
Scenario of the Child
|
|
|
100.201
Our scenario, titled "Experimentally Certified Scientific
Proofs," opens with
a child standing outdoors, glancing all around, pausing
to look more intently at an
aggregate of generalized somethings, and finally focusing
upon a special case something:
|
|
|
100.30
Omnirational Subdividing
|
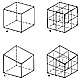 Fig. 100.301 |
100.301
Omniquadrilaterally interconnecting the mid-edge-points
of any dissimilarly-
edge-lengthed quadrilateral polygon always produces
four dissimilar quadrangles.
Omnitriangularly interconnecting the mid-edge-points
of any dissimilarly-edge-lengthed
triangle always produces four similar triangles.
(See Fig. 990.01.) Whereas
omniinterconnecting the mid-edge-points of a cube always
subdivides the cube into eight
similarly equiedged cubes, interconnecting the mid-edge-points
of any dissimilarly-edge-
lengthed quadrangular-faced hexahedra always subdivides
the hexahedron into eight
always dissimilar, quadrangular-faced hexahedra.
(See Fig. 100.301.)
|
|
|
100.3011
Necklace: Here we observe the sequence of the child's
necklace ( Sec. 608).
The child starts with an enlargement of his mother's
necklace consisting of a dozen half-
inch-by- 12-inch aluminum tubes strung tightly together
on dacron cords. The child drapes
the necklace over his shoulders to assume various shapes.
Then, removing one tube at a
time, he finds that the necklace remains flexible .
. . until all but the last three are removed
and__as a triangle__it suddenly holds its shape. (Thus
we arrive at the triangular definition
of a structure.)
|
|
|
100.302
A triangle is a microaltitude tetrahedron with its
apex almost congruent with
one of its base triangle's vertexes. A right-angled
triangle, an isosceles triangle, and a
scalene triangle are all the same triangle. The seeming
difference in edge lengths and
angles is a consequence only of shifting the base-plane
locus of the observer.
|
|
|
100.303
Most economically intertriangulating the midpoints
of any regular equiedged
or any dissimilarly edged tetrahedra will always subdivide
that tetrahedron into four similar
tetrahedra and one octahedron whose volume is always
four times that of any of the four
similar and equivolumed tetrahedra.
|
|
|
100.304
Cheese Tetrahedron: If we make all the symmetrical
Platonic solids of firm
cheese, and if we slice the cube parallel to one of
its faces, the remaining hexahedron is no
longer equiedge-lengthed. So too with all the other
Platonic solids__the dodecahedron,
the octahedron, or the icosahedron__with one, and only
one, exception: the tetrahedron.
The cheese tetrahedron may be sliced parallel to any
one, or successively all four, of its
faces without losing its basic symmetry; ergo, only
the tetrahedron's four-dimensional
coordination can accommodate asymmetric aberrations
without in any way disrupting the
symmetrical integrity of the system.
|
|
|
100.310
Two Tetra into Cube: The child wants to get inside
things. What is the
minimum something it can get inside of? The necklace
tetrahedron strung together with
long-tube-beads. A child tries the necklace cube, and
it collapses. The child then takes the
edge tubes of the collapsed cube and reassembles them
as an octahedron__which holds
its shape. The child also takes two sets of six tubes
and makes two tetrahedra producing
an omnitriangulated superficially induced cube with
eight corners.
|
|
|
100.320
Modular Subdivision of the Cosmic Hierarchy
|
|
|
100.321
Any four points in Universe are always most economically
interrelated by an
ever-transforming tetrahedron, the whole, low-order,
rational volume of whose primitive,
cosmic, equiwavelengthed-and-frequenced corresponding
vector equilibrium, cube,
octahedron, rhombic triacontahedron, and rhombic dodecahedron__stated
in
tetravolumes__are always 1, 2 ½, 2 ½ , 3, 4, 5, 6
__which
hierarchy of constituent geometrical
structures remains eternally invariable.
(See Table 1033.192.)
|
|
|
100.322
The omnirational subdivision of any regular or irregular
tetrahedron by the
systemic triangular interconnecting of the tetrahedron's
similarly frequenced, modular
subdivision points of its six edges, respectively, will
always subdivide the tetrahedron into
the same rationally volumed geometrical constituents
constituting the cosmic hierarchy
and its A and B Quanta Modules as well as its T, E,
and S Modules.
|
|
|
100.323
Only the tetrahedron can accommodate the asymmetric
aberrations of
otherness without losing the integrity of its own four-dimensional
symmetry and its
subdivisible volumetric rationality. The asymmetric
aberrations of otherness are essential
to awareness, awareness being the minimum statement
of the experience life. In the
accommodation of asymmetric aberration the tetrahedron
permits conceptual focus upon
otherness, which is primitively essential to the experience
of life, for it occasions life's
initial awareness.
(See Fig. 411.05.)
|
|
|
100.330
"Me" Ball
|
|
|
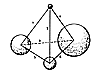
100.331
Here we observe the child taking the "me" ball
(Sec. 411) and running
around in space. There is nothing else of which to be
aware; ergo, he is as yet unborn.
Suddenly one "otherness" ball appears. Life begins.
The two balls are mass-interattracted;
they roll around on each other. A third ball appears
and is mass-attracted; it rolls into the
valley of the first two to form a triangle in which
the three balls may involve-evolute. A
fourth ball appears and is also mass-attracted; it rolls
into the "nest" of the triangular
group. . . and this stops all motion as the four balls
become a self-stabilized system: the
tetrahedron.
(SeeFig. 411.05.)
|
|
|
100.40
Finite Event Scenario
|
|
|
100.401
Events are changes of interrelationships.
|
|
|
100.402
Events are changes of interrelationships between a
plurality of systems or
between constituents of any one system. Events are changes
of interrelationships, between
any one of the separate "thing" system's constituent
characteristics__a minimum thing has
separable parts. A thing is always special case. Special
cases always have time-frequency
relative sizing; whereas the minimum system__the tetrahedron__is
generalized,
prefrequency, timeless, yet conceptual, ergo, does not
have separable parts__but being
primitive and timeless does have primitive fractionability
into structurally conceptual,
timeless, omnirationally accountable, symmetrical, differential
polyhedra of the cosmic
hierarchy.
|
|
|
100.403
The cosmic hierarchy is comprised of the tetrahedron's
inherent,
intertransformable interrelationships__four active, four
passive__all of which occur within
the six primitive, potential, omnidirectional vectorial
moves found in each primitive
system`s (timeless) event potential.
|
|
|
100.41
Foldability of Triangles into Tetrahedra
|
|
|
100.411
Every triangle is always a projected tetrahedron. Any
triangle having no
angle greater than 90 degrees can be folded into a tetrahedron.
No squares or quadrangles
may be folded into a hexahedron.
|
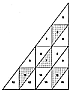 Fig. 100.412 |
100.412
The scalene right triangle is a limit case that folds
into an almost-flat
tetrahedron. (See Fig. 100.412. )
|
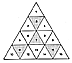 Fig. 100.413 |
100.413
The equiangular triangle folds into a regular tetrahedron
consisting of four
similar, equivolume, regular tetrahedra. Their total
volume equals the volume of the
central octahedron (inadvertently described). (See Fig.
100.413.)
|
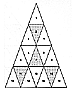 Fig. 100.414 |
100.414
The isosceles triangle, with all angles less than 90
degrees, folds into an
irregular tetrahedron consisting of four similar irregular
tetrahedra. Their total volume
equals the volume of the central irregular octahedron
(inadvertently described). (See Fig. 100.414.)
|
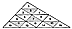 Fig. 100.415 |
100.415
Unfoldable Limit: The scalene triangle, having one
angle greater than 90
degrees, will not fold into a tetrahedron, but it consists
of 16 similar triangles. (See Fig. 100.415.)
|
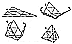 Fig. 100.416 |
100.416
The triangle folded into a tetrahedron inadvertently
describes the four
exposed faces of the tetrahedron's internal octahedron.
(See Figs; 100.416A-D.)
|
|
|
100.50
Constant Triangular Symmetry
|
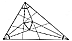 Fig. 100.51 |
100.51
Dr. Frank Morley, a professor of mathematics at Johns
Hopkins University,
was the author of a theorem on triangular symmetry:
The three interior intersection points
of the trisectors of any triangle's three angles will
always describe an equiangular triangle.
It may be demonstrated graphically as in Fig. 100.51.
This theorem is akin to the
tetrahedral coordinate system of synergetics
(Sec. 420),
which describes how the
superficial dissimilarities and aberrations of the tetrahedron
in no way alter any of its
constant symmetries of omnirational subdivisioning .
|
|
|
100.60
Finite Episoding
|
|
|
100.61
Nonunitarily conceptual but finite Scenario Universe's
only separate,
differently enduring, and only overlappingly occurring,
conceptual episodes, their scenery,
costumes, and character parts__all being special case
and temporal__are each and all
demonstrably separable__ergo, finite__and only altogether
coordinate, to provide the
ever-aggregating finiteness of Scenario Universe's complex,
nonsimultaneous__ergo,
nonunitarily conceptual__episodes.
|
|
|
100.62
This moment in the evolutionary advance and psychological
transformation
of humanity has been held back by non-physically-demonstrable__ergo
non-
sensorial__conceptionless mathematical devices and by
the resultant human
incomprehensibility of the findings of science. There
are two most prominent reasons for
this incomprehensibility: The first is the non-physically
demonstrable mathematical tools.
The second is our preoccupation with the sense of static,
fixed "space" as so much
unoccupied geometry imposed by square, cubic, perpendicular,
and parallel attempts at
coordination, rather than regarding "space" as being
merely systemic angle-and-frequency
information that is presently non-tuned-in within the
physical, sensorial range of tunability
of the electromagnetic sensing equipment with which
we personally have been organically
endowed.
|
|
|
100.63
The somethingness here and the nothingness there of
statically interarrayed
"space" conceptioning is vacated as we realize that
the infratunable is subvisible high-
frequency eventing, which we speak of as matter, while
the ultratunable is radiation, which
we speak of as space. The tunable is special case, sensorially
apprehensible episoding.
|
| Next Section: 101.00 |
