1033.030 Untenable Equilibrium Compulsion
1033.031 In the 20-tetravolume vector equilibrium we have four passive and four active tetrahedra vertexially interconnected. The eight tetrahedra have a total of 32 vertexes. In the 20-tetravolume vector equilibrium each tetrahedron has three of its vertexial somethings outwardly arrayed and one vertexial something inwardly arrayed. Their 24 externally arrayed vertexes are congruently paired to form the 12 vertexes of the vector equilibrium, and their eight interior vertexial somethings are nuclear congruent; ergo, four-forcedly-more-vector-interconstrained than any of their externally paired vertexial something sets: an untenable equilibrium compulsion (UEC). (Compare Secs. 1012.11 and 1224.13.)
1033.032 The untenable equilibrium compulsion (UEC) inherently impels the nucleus toward and through any of the nucleus's eight externally subtended triangular windows, the three corners of each of which are two-tensor-restrained (six tensors per triangular window) by the gravitationally embracing, circumferentially closed tensors. This empowers the nuclear eightfold-congruent somethings to exit pulsatingly through the windows to a distance one-half that of the altitude of the regular tetrahedron, which is describable to the eight divergent points by mounting outwardly of the eight Eighth- Octahedra on each of the eight triangular window frames of the vector equilibrium, which thereby describe the cube of 24 tetravolumes (i.e., eight of the primitive, Duo-Tet- described cubes of three tetravolumes). These eight external pulsative points are inherently center-of-volume terminalled when nuclear systems are closest packed with one another. Thus we find the total nuclear domain of Universe to have a tetravolume of 24. When the vector equilibrium nucleus has no closest-packed-around-it, nucleated vector equilibrium systems, then the eightfold nuclear impelment works successively to expel its energies pulsatingly and radiantly through all eight of its windows.
1033.10 Octave System of Polyhedral Transformations
1033.101 The systematic outsideness is the macrountuned: the ultratunable. The systemic insideness is the micrountuned: the infratunable. The system is the discretely tuned-in conceptuality.
1033.102 The closest-packed spheres are simply the frequencies that are activated, that get into closest proximity as a continuum of the outsideness:
__ the critical proximity spherical zone, which is fall-in-here or fall-in-there or independently in orbit for shorter or longer time spans;
__ the boundary layer;
__ the mass-interattractively tensioned (trampoline) field, which is as deeply near as any proximate systems can come to "tangency";
__ the threshold zone of tuned-in but non-frequency-differentialed; when a system is at the threshold, it is non-frequency-modulated, hence only a point-to-able noise or gray, nondescript color.
1033.103 If there were a geometric outsideness and insideness, we would have a static geometrical Universe. But since the insideness and outsideness are the as-yet-untuned-in or no-longer-tuned-in wavelengths and their frequencies, they require only Scenario Universe, its past and future. Only the NOW conceptualizing constitutes a geometry__the immediate conceptual, special-case, systemic episode in a scenario of nonunitarily conceptual, nonsimultaneous, and only partially overlapping, differently enduring, differently magnituded, special-case, systemic episodes, each in itself a constellation of constellations within constellations of infra- or ultratunably frequenced, special case frequenced systems (Compare Sec. 321.05.)
1033.104 The isotropic-vector-matrix-field has an infinite range of electromagnetic tunings that are always multiplying frequency by division of the a priori vector equilibrium and its contained cosmic hierarchy of timeless-sizeless primitive systems' unfrequenced state. At maximum their primitive comprehensive domain is that of the six-tetravolume, 24-A-and-B-quanta-moduled, unfrequenced rhombic dodecahedron, the long axis of whose 12 diamond faces is also the prime vector length of the isotropic vector matrix. At primitive minimum the unfrequenced state is that of the six-A-and-B-quanta-moduled Syte. Both the maximum and minimum, primitive, greatest and least primitive common divisors of Universe may be replicatively employed or convergently composited to produce the isotropic vector matrix field of selectable frequency tunability, whose key wavelength is that of the relative length of the uniform vector of the isotropic vector matrix as initially selected in respect to the diameter of the nucleus of the atom.

Fig. 1033.11 		1033.11 Every electromagnetic wave propagation generates its own cosmic field. This field is a four-dimensional isotropic vector matrix that can be readily conceptualized as an aggregation of multilayered, closest-packed, unit-radius spheres. (See Fig. 1033.111A.) Unit-radius spheres pack tangentially together most closely in 60-degree intertriangulations. Atoms close-pack in this manner. The continuum of inherent outsideness of all systems enters every external opening of all closest-packed, unit-radius sphere aggregates, permeating and omnisurrounding every closest-packed sphere within the total aggregate. Between the closest-packed, unit-radius spheres the intervening voids constitute a uniform series of unique, symmetrical, curvilinear, geometrical shapes, and the successive centers of volumes of those uniform phase voids are uniformly interspaced__ the distance between them being always the same as the uniform distances between adjacent closest-packed spheres.

Fig. 1033.111A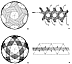

Fig. 1033.111B 		1033.111 Each of the closest-packed, unit-radius spheres is itself a geodesic sphere, a spherical sieve with triangular openings: a tetra-, octa-, or icosasphere of some frequency of modular subdivision. (Compare the fallacy of the Greek sphere as described at Secs. 981.19, 1022.11-13, 1106.22, and 1107.21.) Wherefore, each of the closest-packed spheres is permeable by higher-frequency, shorter-wavelength, electromagnetic propagations; ergo, appropriately frequenced fields may pass through the isotropic vector matrix's electromagnetic field of any given wavelengths without interference. Not only does each closest-packed sphere consist of a plurality of varifrequenced vertices interconnected by chords that define the triangular sieve, but also these vertexial somethings are mass-interattractively positioned and have their own boundary layer (trampoline) cushions; ergo, they are never in absolute tangency.
1033.112 The isotropic vector matrix grid illustrates that frequency multiplication may be accomplished only by division. The unit-radius spheres of the isotropic vector matrix electromagnetic fields close-pack in four planes of symmetry, permitting four-dimensional electromagnetic wavebands. The three-way, spherical, electromagnetic, basketry interweaving is illustrated at Fig. 1033.111B. There are six great-circle equators of the six axes formed by the 12 vertices of the spherical icosahedron. The centers of area of the spherical triangles thus formed describe the terminals of the electromagnetic waveband widths. The widths of the bands of frequency tunability are determined by the truncatability of the spherical icosahedron's six bands as they run between the centers of area of the adjacent triangles.
1033.113 Note that the centers of area of the adjacent spherical triangles are alternately staggered so as to define a broad path within which the electromagnetic waveband is generated.
1033.120 Click-stop Subdivisioning
1033.121 In synergetic geometry we witness the transformation of all spheres into their local complementary inter-void domains as the local inter-void domains transform into closest-packed, unit-radius spheres. (See Fig. 1032.31.) The multifrequenced tetrahedral, octahedral, and icosahedral geodesic subdivisioning of spherical projections of the primitive polyhedral systems describes how the complex interbonding of substances occurs; it is further described by the varying radii of the closest-packed spheres and the complex of isotropic vector matrixes required to accommodate the varying radii as well as their ultra- and infrapermeating: this elucidates the resonance of substances as well as the unique electromagnetic frequencies of chemical elements. Here is the grand synergetic nexus integrating electromagnetics, chemistry, and topology.
1033.122 Synergetics arouses human awareness of the always-and-only-co-occurring, non-tuned-in cosmic complementations of our only-from-moment-to-moment systematically tuned-in conceptionings. Synergetics' always symmetrical, complementarily expanding and contracting intertransformings disclose a succession of "local way stations." Progressive arrival at these convergent-divergent "way station" states discloses a succession of immediately neighboring, larger-to-smaller, symmetrical polyhedra of diminishingly numbered topological characteristics, which all together constitute a cosmic hierarchy of symmetrical, rationally volumed, most primitive, pattern-stabilization states. Superficially the states are recognizable as the family of Platonic polyhedra.
1033.123 Throughout the convergent phase of the transformation continuum, all the vertices of these successive Platonic forms and their intertransformative phases are always diminishingly equidistant from the same volumetric center. The omnisymmetrical contraction is accommodated by the angular closing__scissor-hinge-wise__of immediately adjacent edges of the polyhedra. The vertices of each of these intertransforming symmetric states, as well as their intermediate transforms, are always positioned in a sphere that is progressively expanding or contracting__depending on whether we are reading the cosmic hierarchy as energetic volumes from 1 to 24 or from 24 to 1.
1033.124 As the originally omnisymmetrical, 20-tetravolume vector equilibrium of 12 vertices, 14 faces, and 24 vector edges shrinks its vertex-described spherical domain, it may receive one quantum of energy released entropically by some elsewhere-in-Universe entropic radiation, as most frequently occurring when octahedra of matter are precessed and the octahedron's tetravolume 4 is reduced to tetravolume 3 (see Octahedron as Conservation and Annihilation Model, Sec. 935), the tetrahedron thus annihilated being one quantum lost entropically without any alteration of the Eulerean topological characteristics as an octahedron. Since each quantum consists of six vector edges that can now be entropically dispersed, they may be syntropically harvested by the 20-tetravolume vector equilibrium, and, constituting one quantum of energy, they will structurally stabilize the shrinking 20-tetravolume vector equilibrium 4-tetravolume octahedron system in the intermediate symmetrical form of the icosahedron. As the icosahedron of 12 vertices, 20 faces, and 30 edges (24 + 6) shrinks its spherical domain, it can do so only by compressing the one energy quantum of six syntropically captured vector edges into the six vertical somethings of the octahedron, thereby allowing 12 faces to unite as six__all the while the icosahedron's ever-shrinking spherical surface pattern alters uniformly, despite which its topological inventory of 12 vertices, 14 faces, and 24 edges remains constant until the simultaneous moment of vertex, face, and edge congruence occurs. Simultaneously each of the paired vertices and edges__as well as the six compressed vector edges__now appears as one; and each of the congruent pairs is now topologically countable only as one in this instance as the six vertices, eight faces, and 12 edges of the suddenly realized octahedron of tetra-volume 4.
1033.125 The simultaneous vanishing of the previously shuttling and lingering topological characteristics from the previously stable icosahedral state, and the instant appearance of the next neighboring state__the octahedron, in its simplest and completely symmetrical condition__is what we mean by a "click-stop" or "way station" state.
1033.126 Assessing accurately the "click-stop" volumes of the intertransformative hierarchy in terms of the volume of the tetrahedron equaling one, we find that the relative tetravolumes of these primitive polyhedra__when divergent__are successively, 1, 2 1/2, 3, 22, 5, 6, 20, 24, and then__converging__from 24, 20, 6, 5, 22, 3, 2 l/2, 1. These omnirational, whole-number, "click-stop" volumes and their successive topological characteristic numbers elegantly introduce__and give unique volumetric shape to__each of all of the first four prime numbers of Universe: 1, 2, 3, 5. (Compare Sec. 100.321.)
1033.127 These click-stop, whole-tetravolumed, symmetrical geometries have common centers of volume, and all are concentrically and intersymmetrically arrayed within the rhombic dodecahedron. In this concentric symmetric array they constitute what we call the cosmic hierarchy of primitive conceptuality of thought and comprehension. Intuitively hypersensitive and seeking to explain the solar system's interplanetary behaviors, Johannes Kepler evolved a concentric model of some of the Platonic geometries but, apparently frustrated by the identification of volumetric unity exclusively with the cube, failed to discover the rational cosmic hierarchy__it became the extraordinary experience of synergetics to reveal this in its first written disclosure of 1944.
1033.128 It is visually manifest both between and at the "click-stop" states that the smooth intertransforming is four-dimensional, accommodated by local transformations around four axes of system symmetry. The systems' vertices always remain spherically arrayed and describe a smooth, overall-spheric-continuum-contraction from the largest to the smallest tune-in-able-by-the-numbers system states occurring successively between the beyond-tune-in-able system ranges of the macronothingness and the beyond-tune-in-able micronothingness.
Next Section: 1033.180
Copyright © 1997 Estate of R. Buckminster Fuller