Jitterbug Transformation and Annihilation
|
|
938.00
Jitterbug Transformation and Annihilation
|
|
|
938.10
Positive and Negative Tetrahedra
|
|
|
938.11
The tetrahedron is the minimum-limit-case structural
system of Universe (see
Secs.
402
and
620). The tetrahedron consists of two
congruent tetrahedra: one concave,
one convex. The tetrahedron divides all of Universe
into all the tetrahedral nothingness of
all the cosmic outsideness and all the tetrahedral nothingness
of all the cosmic insideness
of any structurally conceived or sensorially experienced,
special case, uniquely considered,
four-starry-vertex-constellared, tetrahedral system
somethingness of human experience,
cognition, or thinkability.
|
|
|
938.12
The tetrahedron always consists of four concave-inward
hedra triangles and
of four convex-outward hedra triangles: that is eight
hedra triangles in all. (Compare Fig.
453.02.)
These are the same eight__maximally deployed
from one another__equiangular
triangular hedra or facets of the vector equilibrium
that converge to differential
inscrutability or conceptual zero, while the eight original
triangular planes coalesce as the
four pairs of congruent planes of the zero-volume vector
equilibrium, wherein the eight
exterior planes of the original eight edge-bonded tetrahedra
reach zero-volume, eightfold
congruence at the center point of the four-great-circle
system. (Compare Fig.
453.02.)
|
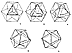 Fig. 938.13 |
938.13
The original__only vertexially single-bonded, vectorially
structured__triangles of the vector-equilibrium jitterbug
transform by symmetrical
contraction from its openmost vector-equilibrium state,
through the (unstable-without-six-
additional-vector inserts; i.e., one vectorial quantum
unit) icosahedral stage only as
accommodated by the nuclear sphere's annihilation, which
vanished central sphere
reappears transformedly in the 30-vector-edged icosahedron
as the six additional external
vectors added to the vector equilibrium to structurally
stabilize its six "square" faces,
which six vectors constitute one quantum package. (See
Fig. 938.13.)
|
|
|
938.14
Next the icosahedron contracts symmetrically to the
congruently vectored
octahedron stage, where symmetrical contraction ceases
and precessional torque reduces
the system to the quadrivalent tetrahedron's congruent
four positive and four negative
tetrahedra. These congruent eight tetrahedra further
precess into eight congruent zero-
altitude tetrahedral triangles in planar congruence
as one, having accomplished this
contraction from volume 20 of the vector equilibrium
to volume 0 while progressively
reversing the vector edges by congruence, reducing the
original 30 vector edges (five
quanta) to zero quanta volume with only three vector
edges, each consisting of eight
congruent vectors in visible evidence in the zero-altitude
tetrahedron. And all this is
accomplished without ever severing the exterior, gravitational-embracing
bond integrity of
the system. (See Figs.
461.08
and
1013.42.)
|
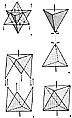 Fig. 938.15 |
938.15
The octahedron is produced by one positive and one
negative tetrahedron.
This is done by opening one vertex of each of the tetrahedra,
as the petals of a flower are
opened around its bud's vertex, and taking the two open-flowered
tetrahedra, each with
three triangular petals surrounding a triangular base,
precessing in a positive-negative way
so that the open triangular petals of each tetrahedron
approach the open spaces between
the petals of the other tetrahedron, converging them
to produce the eight edge-bonded
triangular faces of the octahedron. (See Fig.
938.15.)
|
 Fig. 938.16 |
938.16
Because the octahedron can be produced by one positive
and one negative
tetrahedron, it can also be produced by one positive
tetrahedron alone. It can be produced
by the four edge-bonded triangular faces of one positive
tetrahedron, each being unbonded
and precessed 60 degrees to become only vertex-interbonded,
one with the other. This
produces an octahedron of four positive triangular facets
interspersed symmetrically with
four empty triangular windows. (See Fig.
938.16.)
|
940.00
Hierarchy of Quanta Module Orientations
|
|
940.10
Blue A Modules and Red B Modules
|
|
|
940.11
A Modules: We color them blue because the As are energy
conservers, being
folded out of only one triangle.
|
|
|
940.12
B Modules: We color them red because the Bs are energy
distributors, not
being foldable out of only one triangle.
|
|
|
940.13
This coloring will provide quick comprehension of
the energy behaviors
unique to the various geometrical systems and their
transformations__for instance, in the
outermost module layer shell of the vector equilibrium,
all the triangular faces will be blue
and all the square faces will be red, indicating that
the eight tetrahedra of the vector
equilibrium are conserving the system's structural integrity
and will permit export of
energy from the square faces of the system without jeopardizing
the system's structural
integrity.
|
|
|
941.00
Relation of Quanta Modules to Closest-Packed Sphere
Centers
|
|
|
942.01
Illustrations of the A and B Quanta Modules may be
made with spherical
segment arcs of unit radius scribed on each of their
three triangular faces having a
common vertex at the sphere's center. The common center
of those circular arcs lies in
their respectively most acute angle vertexes; thus,
when assembled, those vertexes will lie
in the centers of the closest-packed spheres of which
each A and B Quanta Module
embraces a part, 1/l44th of a sphere, as well as its
proportional part of the space between
the closest-packed spheres.
|
|
|
942.00
Progression of Geometries in Closest Packing
|
|
|
942.01
Two balls of equal radius are closest packed when
tangent to one another,
forming a linear array with no ball at its center. Three
balls are closest packed when a third
ball is nested into the valley of tangency of the first
two, whereby each becomes tangent to
both of the other two, thus forming a triangle with
no ball at its center. Four balls are
closest packed when a fourth ball is nested in the triangular
valley formed atop the closest-
packed first three; this fourth-ball addition occasions
each of the four balls becoming
tangent to all three of the other balls, as altogether
they form a tetrahedron, which is an
omnidirectional, symmetrical array with no ball at its
center but with one ball at each of its
four comers. (See Sec.
411.)
|
|
|
942.02
Four additional balls can be symmetrically closest
packed into the four nests
of the closest-packed tetrahedral group, making eight
balls altogether and forming the star
tetrahedron, with no ball at its center.
|
|
|
942.03
Five balls are closest packed when a fifth ball is
nested into the triangular
valley on the reverse side of the original triangular
group's side within whose triangular
valley the fourth ball had been nested. The five form
a polar-symmetry system with no ball
at its center.
|
|
|
942.04
Six balls are closest packed when two closest-packed
triangular groups are
joined in such a manner that the three balls of one
triangular group are nested in the three
perimeter valleys of the other triangular group, and
vice versa. This group of six balls is
symmetrically associated, and it constitutes the six
corners of the regular octahedron, with
no ball at its center.
|
|
|
942.05
Eight additional balls can be mounted in the eight
triangular nests of the
octahedron's eight triangular faces to produce the star
octahedron, a symmetrical group
of 14 balls with no ball at the group's center.
|
|
|
942.10
Tetrahedron: The tetrahedron is composed exclusively
of A Modules
(blue), 24 in all, of which 12 are positive and 12 are
negative. All 24 are asymmetrical,
tetrahedral energy conservers.3 All the tetrahedron's
24 blue A Modules are situate in its
only one-module-deep outer layer. The tetrahedron is
all blue: all energy-conserving.
(Footnote 3: For Discussion of the self-containing energy-reflecting patterns of single triangles that fold into the tetrahedron __symmetrical or asymmetrical__ see Sec. 914 and 921.) |
|
|
942.11
Since a tetrahedron is formed by four mutually tangent
spheres with no
sphere at its center, the A Modules each contain a portion
of that sphere whose center is
congruent with the A Module's most acute comer.
|
|
|
942.12
The tetrahedron is defined by the lines connecting
the centers of the
tetrahedron's four corner spheres. The leak in the tetrahedron's
corners elucidates entropy
as occasioned by the only-critical-proximity but nontouching
of the tetrahedron's corners-
defining lines. We always have the twisting__the vectorial
near-miss__at the corners of the
tetrahedron because not more than one line can go through
the same point at the same
time. The construction lines with which geometrical
entities are structured come into the
critical structural proximity only, but do not yield
to spontaneous mass attraction, having
relative Moon-Earth-like gaps between their energy-event-defining
entities of realization.
(See Sec.
921.15.)
|
|
|
942.13
The tetrahedron has the minimum leak, but it does
leak. That is one reason
why Universe will never be confined within one tetrahedron,
or one anything.
|
|
|
942.15
Quarter-Tetrahedra: Quarter-Tetrahedra have vector-edged,
equiangled,
triangular bases that are congruent with the faces of
the regular tetrahedron. But the apex
of the Quarter-Tetrahedron occurs at the center of volume
of the regular tetrahedron.
|
|
|
942.16
The Quarter-Tetrahedra are composed of three positive
A Quanta Modules
and three negative A Quanta Modules, all of which are
asymmetrical tetrahedra. We
identify them as six energy quanta modules. These six
energy quanta modules result when
vertical planes running from the three vertexes to their
three opposite mid-edges cut the
Quarter-Tetrahedron into six parts, three of which are
positive and three of which are
negative.
|
|
|
942.17
The triangular conformation of the Quarter-Tetrahedron
can be produced by
nesting one uniradius ball in the center valley of a
five-ball-edged, closest-packed,
uniradius ball triangle. (See Illus.
415.55C.) The four
vertexes of the Quarter-Tetrahedron
are congruent with the volumetric centers of four uniradius
balls, three of which are at the
comers and one of which is nested in the valley at the
center of area of a five-ball-edged,
equiangle triangle.
|
|
|
942.18
The Quarter-Tetrahedron's six edges are congruent
with the six lines of sight
connecting the volumetric centers of the base triangle's
three uniradius corner balls, with
one uniradius ball nested atop at the triangle's center
of area serving as the apex of the
Quarter-Tetrahedron.
|
|
|
942.20
Isosceles Dodecahedron: The isosceles dodecahedron
consists of the
regular tetrahedron with four Quarter-Tetrahedra extroverted
on each of the regular
tetrahedron's four triangular faces, with the extroverted
Quarter-Tetrahedra's volumetric
centers occurring outside the regular tetrahedron's
four triangular faces, whereas the
central nuclear tetrahedron's four Quarter Tetrahedra
are introverted with their volumetric
centers situate inwardly of its four outer, regular,
equiangled, triangular faces.
|
|
|
942.21
The isosceles dodecahedron is composed of 48 blue
A Modules, 24 of which
are introverted; that is, they have their centers of
volume inside the faces of the central,
regular tetrahedron and constitute the nuclear layer
of the isosceles dodecahedron. An
additional 24 extroverted A Modules, with their volumetric
centers occurring outside the
four triangular faces of the central tetrahedron, form
the outermost shell of the isosceles
dodecahedron. The isosceles dodecahedron is all blue
both inside and outside.
|
|
|
942.30
Octahedron: The octahedron or "Octa" is composed of
96 energy quanta
modules of which 48 are red B Quanta Modules and 48
blue A Quanta Modules. It has
two module layers, with the inner, or nuclear, aggregate
being the 48 red Bs and the outer
layer comprised of the 48 blue As. The octahedron is
all blue outside with a red nucleus.
|
|
|
942.31
The octahedron has distributive energies occurring
at its nucleus, but they
are locked up by the outer layer of A Modules. Thus
the tendency of the 48 red B Module
energy distributors is effectively contained and conserved
by the 48 blue A Module
conservators.
|
|
|
942.40
Cube: The cube is composed of a total of 72 energy
quanta modules, of
which there are 48 blue A Modules and 24 red B Modules.
The cube is produced by
superimposing four Eighth-Octahedra upon the four equiangle
triangular faces of the
regular tetrahedron.
|
|
|
942.41
The cube is three module layers deep, and the layering
occurs around each of
its eight corners. All of the cube's nuclear and outer-shell-modules
three-layer edges are
seen to surface congruently along the six diagonal seams
of the cube's six faces. The inner
nucleus of the cube consists of the blue introverted
tetrahedron with its 24 A Modules.
This introverted tetrahedron is next enshelled by the
24 blue A Modules extroverted on the
introvert nuclear tetrahedron's four faces to form the
isosceles dodecahedron. The third
and outer layer of the cube consists of the 24 red B
Modules mounted outward of the
isosceles dodecahedron's 24 extroverted A Modules.
|
|
|
942.42
Thus, as it is seen from outside, the cube is an all-red
tetrahedron, but its
energy-distributive surface layer of 24 red B Modules
is tensively overpowered two-to-
one and cohered as a cube by its 48 nuclear modules.
The distributors are on the outside.
This may elucidate the usual occurrence of cubes in
crystals with one or more of their
corners truncated.
|
|
|
942.43
The minimum cube that can be formed by closest packing
of spheres (which
are inherently stable, structurally speaking) is produced
by nesting four balls in the
triangular mid-face nests of the four faces of a three-layer,
ten-ball tetrahedron, with no
ball at its volumetric center. This produces an eight-ball-cornered
symmetry, which
consists of 14 balls in all, with no ball at its center.
This complex cube has a total of 576 A
and B Modules, in contradistinction to the simplest
tetra-octa-produced cube constituted
of 72 A and B Modules.
|
|
|
942.50
Rhombic Dodecahedron: The rhombic dodecahedron is
composed of 144
energy quanta modules. Like the cube, the rhombic dodecahedron
is a three-module
layered nuclear assembly, with the two-layered octahedron
and its exclusively red B
Moduled nucleus (of 48 Bs) enveloped with 48 exclusively
blue A Modules, which in turn
are now enclosed in a third shell of 48 blue A Modules.
Thus we find the rhombic
dodecahedron and the cube co-occurring as the first
three-layered, nuclearly centered
symmetries-with the cube having its one layer of 24
red B Modules on the outside of its
two blue layers of 24 A Modules each; conversely, the
rhombic dodecahedron has its two
blue layers of 48 A Modules each on the outside enclosing
its one nuclear layer of 48 red
B Modules.
|
|
|
942.51
The most simply logical arrangement of the blue A
and red B Modules is one
wherein their 1/144th-sphere-containing, most acute
corners are all pointed inward and
join to form one whole sphere completely contained within
the rhombic dodecahedron,
with the contained-sphere's surface symmetrically tangent
to the 12 mid-diamond facets of
the rhombic dodecahedron, those 12 tangent points exactly
coinciding with the points of
tangency of the 12 spheres closest-packed around the
one sphere. (For a discussion of the
rhombic dodecahedron at the heart of the vector equilibrium,
see Sec.
955.50.)
|
|
|
942.60
Vector Equilibrium: The vector equilibrium is composed
of 336 blue A
Modules and 144 red B Modules for a total of 480 energy
quanta modules: 480 = 25 × 5 ×
3. The eight tetrahedra of the vector equilibrium consist
entirely of blue A Modules, with a
total of 48 such blue A Modules Lying in the exterior
shell. The six square faces of the
vector equilibrium are the six half-octahedra, each
composed of 24 blue As and 24 red Bs,
from which inventory the six squares expose 48 red B
Modules on the exterior shell. An
even number of 48 As and 48 Bs provide an equilibrious
exterior shell for the vector
equilibrium: what an elegance! The distributors and
the conservators balance. The six
square areas' energies of the vector equilibrium equal
the triangles' areas' energies. The
distributors evacuate the half-octahedra faces and the
basic triangular structure survives.
|
|
|
942.61
The vector equilibrium's inherently symmetrical, closest-packed-sphere
aggregate has one complete sphere occurring at its volumetric
center for the first time in
the hierarchy of completely symmetrical, closest-packed
sets. In our multilayered,
omniunique patterning of symmetrical nuclear assemblies,
the vector equilibrium's inner
layer has four energy quanta modules in both its eight
tetrahedral domains and its six half-
octahedra domains, each of which domains constitutes
exactly one volumetric twentieth of
the vector equilibrium's total volume.
|
|
|
942.62
The blue A Modules and the red B Modules of the vector
equilibrium are
distributed in four layers as follows:
|
|
|
942.63
In both of the innermost layers of the vector equilibrium,
the energy-
conserving introvert A Modules outnumber the B Modules
by a ratio of two-to-one. In the
third layer, the ratio is two-to-zero. In the fourth
layer, the ratio of As to Bs is in exact
balance.
|
|
|
942.64
Atoms borrow electrons when they combine. The open
and unstable square
faces of the vector equilibrium provide a model for
the lending and borrowing operations.
When the frequency is three, we can lend four balls
from each square. Four is the greatest
number of electrons that can be lent: here is a limit
condition with the three-frequency and
the four-ball edge. All the borrowing and lending operates
in the squares. The triangles do
not get jeopardized by virtue of lending. A lending
and borrowing vector equilibrium is
maintained without losing the structural integrity of
Universe.
|
|
|
942.70
Tetrakaidecahedron: The tetrakaidecahedron__Lord Kelvin's
"Solid"__is
the most nearly spherical of the regular conventional
polyhedra; ergo, it provides the most
volume for the least surface and the most unobstructed
surface for the rollability of least
effort into the shallowest nests of closest-packed,
most securely self-cohering, allspace-
filling, symmetrical, nuclear system agglomerations
with the minimum complexity of
inherently concentric shell layers around a nuclear
center. The more evenly faceted and the
more uniform the radii of the respective polygonal members
of the hierarchy of
symmetrical polyhedra, the more closely they approach
rollable sphericity. The four-facet
tetrahedron, the six-faceted cube, and the eight-faceted
octahedron are not very rollable,
but the 12-faceted, one-sphere-containing rhombic dodecahedron,
the 14-faceted vector
equilibrium, and the 14-faceted tetrakaidecahedron are
easily rollable.
|
|
|
942.71
The tetrakaidecahedron develops from a progression
of closest-sphere-
packing symmetric morphations at the exact maximum limit
of one nuclear sphere center's
unique influence, just before another nuclear center
develops an equal magnitude
inventory of originally unique local behaviors to that
of the earliest nuclear agglomeration.
|
|
|
942.72
The first possible closest-packed formulation of a
tetrakaidecahedron occurs
with a three-frequency vector equilibrium as its core,
with an additional six truncated,
square-bottomed, and three-frequency-based and two-frequency-plateaued
units
superimposed on the six square faces of the three-frequency,
vector-equilibrium nuclear
core. The three-frequency vector equilibrium consists
of a shell of 92 unit radius spheres
closest packed symmetrically around 42 spheres of the
same unit radius, which in turn
closest-pack enclose 12 spheres of the same unit radius,
which are closest packed around
one nuclear sphere of the same unit radius, with each
closest-packed-sphere shell
enclosure producing a 14-faceted, symmetrical polyhedron
of eight triangular and six
square equiedged facets. The tetrakaidecahedron's six
additional square nodes are
produced by adding nine spheres to each of the six square
faces of the three-frequency
vector equilibrium's outermost 92-sphere layer. Each
of these additional new spheres is
placed on each of the six square facets of the vector
equilibrium by nesting nine balls in
closest packing in the nine possible ball matrix nests
of the three-frequency vector
equilibrium's square facets; which adds 54 balls to
the
|
|
|
942.73
The tetrakaidecahedron consists of 18,432 energy quanta
modules, of which
12,672 are As and 5,760 are Bs; there are 1,008 As and
only 192 Bs in the outermost
layer, which ratio of conservancy dominance of As over
distributive Bs is approximately
two-to-one interiorly and better than five-to-one in
the outermost layer.
|
| Next Section: 943.00 |