Narrative Exposition of Spherical Accommodation
|
|
986.200
Narrative Exposition of Spherical Accommodation
|
|
|
986.201
Consideration 10: The Spheric Experience: Energetic-reality
Accounting vs Abstract-cubic Accounting
|
|
|
986.202
In Synergetics 1, Secs.
962
through
966, I developed
the first-, second-, and
third-power values of my numerical factors for converting
the XYZ coordinate system's
edge lengths, square areas, and cubical volumes to my
1927-discovered synergetic
system's unit VE vectorial edge lengths, triangular
areas, and tetrahedral volumes.3 (See
Table
963.10.)
(Footnote 3: My chart of these conversion factors, which I at first called the Dymaxion constants, was privately published in 1950 at North Carolina State University, and again in 1959 in The Dymaxion World of Buckminster Fuller, written with Robert W. Marks.) |
|
|
986.203
The synergetics coordinate system-in contradistinction
to the XYZ
coordinate system-is linearly referenced to the unit-vector-length
edges of the regular
tetrahedron, each of whose six unit vector edges occur
in the isotropic vector matrix as
the diagonals of the cube's six faces. We also recall
that the eight corners of the cube are
defined and structured omnitriangularly by the symmetrically
interarrayed and concentric
pairs of positive and negative tetrahedra (Figs.
110A
and
110B).
|
|
|
986.204
Since the cube-face diagonal is the edge of the six-vector-edged,
four-
planes-of-symmetry tetrahedron, and since synergetics
finds the unit-vector-edged
tetrahedron to be the simplest structural system in
Universe, the tetrahedron's vector edge
logically becomes the most economically primitive simplex
module of relative length in
synergetics' coordinate system of exploratory reference.
Thus the tetrahedron's unit
vector edge of unity 2 is manifest as nature's coordinate
primitive-length module for
assessing:
second-power triangular area, 22 = 4
as well as for assessing that vector's
third-power tetrahedral volume, 23 = 8,
These areas and volumes become the logical unit of areal and volumetric reference in accounting the relative geometrical area and volume values of the entire hierarchy of primitive, concentrically congruent, symmetrical polyhedra as these naturally occur around any vertex of the isotropic vector matrix, and that matrix's experimentally demonstrable, maximum-limit set of seven axes of polyhedral symmetries, which seven symmetries (Sec. 1040) accommodate and characterize the energetic special case formulations of all great- circle gridding. |
|
|
986.205
The synergetics hierarchy of topological characteristics
as presented in Table
223.64
of Synergetics 1 (which was contracted for with
Macmillan in 1961 and published
by them in 1975), discloses the rational values of the
comprehensive coordinate system of
nature, which my 60-year exploration discovered. In
1944 I published a paper disclosing
this rational system. At that time I was counseled by
some of my scientist friends, who
were aware that I was continuing to make additional
refinements and discoveries, that
premature publication of a treatise of disclosure might
result in the omission of one or
more items of critical information which might be later
discovered and which might make
the difference between scientific acceptance or rejection
of the disclosures. Reminded by
those scientist-artist friends that we have only one
opportunity in a lifetime out of many
lifetimes to publish a prime-science-reorienting discovery,
I postponed publishing a
comprehensive treatise until in 1970, at the age of
75, I felt it could no longer be delayed.
|
|
|
986.206
The eleventh-hour publishing of Synergetics 1 coincided
with my busiest
years of serving other obligations over a period calling
for a vast number of tactical
decisions regarding the methodology of producing what
proved to be a 780-page book.
Typical of the problems to be swiftly resolved are those
shortly to be herewith recounted.
The accounting also discloses the always surprisingly
productive events that ensue upon
mistake-making that are not only discovered and acknowledged,
but are reexplored in
search of the significance of the mistakes' having occurred.
|
|
|
986.207
Because the XYZ-coordinate, three-dimensional system
values are arrived at
by successive multiplying of the dimensions, volume
in that system is an inherently three-
dimensional phenomenon. But in synergetics the primitive
values start holistically with
timeless-sizeless tetrahedral volume unity in respect
to which the cube's primitive value is
3, the octahedron's relative timeless-sizeless value
is 4, the rhombic triacontrahedron's is
5, and the rhombic dodecahedron's is 6. In synergetics,
when time-size special-case
realizations enter into the consideration, then the
(only-interrelated-to-one-another)
primitive volumes of the synergetic hierarchy are multiplied
by frequency of the edge
modulation to the third power. Since innate primitive
volume is a base-times-altitude
three-dimensional phenomenon, and since all the synergetics
hierarchy's time-size
realization volumes are inherently six-dimensional,
I was confronted with an exploratory
tactical quandary.
|
|
|
986.208
The problem was to arrive at the numerical volume value
for the sphere in
the synergetics hierarchy, and the dilemma was whether
I should apply my synergetics'
volumetric constant to the first power or to the third
power of the XYZ-coordinate
system's volumetric values as arrived at by the conventional
XYZ-coordinate system's
method of calculating the volume of a sphere of radius
vector = 1. This operation is
recorded in Sec.
982.55
of Synergetics 1, where I misconceptualized
the operation, and
(without reviewing how I had calculated the constant
for converting XYZ to synergetics)
redundantly took the number 1.192324, which I assumed
(again in mistaken carelessness)
to be the third-power value of the synergetics-conversion
constant, and I applied it to the
volumetric value of a sphere of unit vector diameter
as already arrived at by conventional
XYZ-referenced mathematics, the conventional XYZ-coordinate
volumetric value for the
volume of a sphere of radius 1 being 4.188, which multiplied
by 1.192324 gave the
product 4.99__a value so close to 5 that I thought it
might possibly have been occasioned
by the unresolvability of tail-end trigonometric interpolations,
wherefore I tentatively
accepted 4.99 as probably being exactly 5, which, if
correct, was an excitingly significant
number as it would have neatly fitted the sphere into
the hierarchy of primitive polyhedra
(Sec.
982.61).
My hindsight wisdom tells me that my
subconscious demon latched tightly
onto this 5 and fended off all subconsciously challenging
intuitions.
|
|
|
986.209
But what I had mistakenly assumed to be the third-power
synergetics
constant was in fact the ninth power of that constant,
as will be seen in the following list
of the synergetics constant raised to varying powers:
|
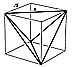 Fig. 986.210 |
986.210
In our always-experimental-evidenced science of geometry
we need only
show ratio of proportion of parts, for parts of primitive
polyhedra have no independent
existence. Ergo, no experimental proof is required for
(square) roots and (square) roots. Though those
numbers are irrational, their irrationality could not
frustrate the falling apart of the
polyhedral parts, because the parts are nonexistent
except as parts of wholes, and exact
proportionality is not required in the structuring.
|
|
|
986.211
Whatever the workings of my subconscious may have been,
the facts remain
that I had erroneously concluded that the 5 was the
tetravolume of the sphere whose
diameter was our unit vector whose value was 2. In due
course I received a letter from a
mathematician, Ramsey Campbell, whose conventional calculations
seemed to show that I
was wrong. But I was not convinced that his conventional
results were not also erroneous,
inasmuch as they had been "cubically" arrived at rather
than tetrahedrally referenced.
|
|
|
986.212
At this point a young associate of mine, Robert Grip__who
was convinced
that I was misconvinced__and who knew that I would alter
my position only as
confronted by physically demonstrable evidence, made
a gallon-sized, water-holding
tetrahedron and a sphere whose diameter was identical
with the prime vector length of the
tetrahedron's edge. The water content-the volume of
the sphere was indeed 4.43
units__0.57 less than 5.
|
|
|
986.213
The cubically-arrived-at spherical volume (A) of a
sphere of diameter equal
to the unit edge of the XYZ coordinate system's cube
is 4.188. To convert that spherical
volume value (A) to that of sphere (B) whose diameter
is equal to the diagonal of the face
of the XYZ system's cube, we multiply the volume of
sphere (A) by the synergetics
hierarchy's volumetric constant, which is obtained by
taking synergetics' unit VE vector
linear constant 1.0198 and raising it to its third-power__or
volumetric__dimension, which
is 1.0198 × 1.0198 × 1.0198, which equals 1.0606. Multiplying
the XYZ system's cube-
edge-diametered (A) sphere's volume of 4.1888 by the
synergetics' volumetric constant of
1.0606 gives us 4.4429, which is the sought-for volume
of the sphere (B). I thanked Mr.
Campbell and acknowledged my error.
|
|
|
986.214
I then said to my mathematical associates, Robert Grip
and Chris Kitrick,
that there is no single item that more effectively advances
research than the unblocking of
our thought processes__through experiential evidence__of
a previously held erroneous
assumption. Wherefore my intuition told me that my error
may have been stubbornly clung
to because there might be something very important to
be discovered in this region of
investigation. There is possibly some enlightening significance
in the fact that I had
intuitively applied (and again forsaking the first correction,
had doubly reapplied) my
third-power synergetics' conversion factor to an already-three-dimensional
cubic-volume
quantation, which on the occasion of these retreatments
had erroneously seemed to me to
be as yet three powers short of the minimum primitive
realizable somethingness.
|
|
|
986.215
Why did I think as I did? Why was I puzzled? I was
not confused about
arithmetical operations per se. We conventionally arrive
at the area of a square by
multiplying the square's edge length by itself, and
we arrive at the volume of a cube by
multiplying its edge length times itself twice__that
is, we identify the square's area by the
second power of its edge length, and we identify a cube's
volume by the third power of its
edge length. All that seems simple and clear . . . until
we discover that the cube does not
exist and cannot exist until it has at least three other
observable attributes: weight,
duration, and temperature. Given the quantitative inputs
for those coordinate factors, the
cube as yet fails to "exist," because as calculated
it is now "solid," and physics has
discovered and proven that no such solid phenomenon
exists; wherefore the cubical
domain has to be substantively populated by atoms which
have a variety of interspacing
and interpositioning behavioral patterns.
|
|
|
986.216
Also, in order to exist the cube must have both tension
and compression
forces so arranged and quantated as to produce a self-stabilizing,
independent behavior in
the presence of the cosmic complex of coexisting force
events. For it to exist there also
must be introduced coordinate factors that account for
the fact that this special case cube
is keeping locatable company with the planet Earth with
which it is traveling around the
Sun at approximately 60,000 miles per hour.
|
|
|
986.217
As the Earth and the Sun whirl circumferentially in
company with the other
hundred billion stars of the galactic system, and as
all the while the galactic system keeps
company with all the now-known billion such galaxies
whose uniformly angled retreat
from one another at an astronomical speed altogether
constitutes what is called the
Expanding Universe . . . if we wrote out the formula
for integrating all those quantities
and for realistically diagramming its geometry and its
dimensions, we would have to admit
that the dimensions of the cube did not as yet produce
existence. There would as yet be
required the set of coordinate factors stating when
and where the cube was born, how old
it was at the moment of its dimensioning, and what its
exact remaining longevity would
be__and with all that, we have not disclosed its smell,
its resonance factor, its
electromagnetic-wave propagation length and frequencies.
My quandary was one of
adequately identifying and calculating the magnitude
of relevant dimensions for the
"considered set" (Section
509).
|
|
|
986.218
My quandary also included, "Which exactly are the attributes
that are being
disclosed by the successive powerings?" With all the
foregoing considerations I resolved
upon the following set as that which I would employ
in publishing Synergetics.
|
|
|
986.219
Since our dimensional control is the prime vector,
and since a vector's
relative size represents mass times velocity, and since
mass has a priori both volume and
weight, it inherently introduces one more dimension
to velocity's a priori two-dimensional
product of time and distance. Ergo, vectors are in themselves
primitive, pre-time-size,
potentially energizable, three-dimensional phenomena.
Any special case time-size
phenomena must also be multiplied by frequency of subdivision
of the primitive system
taken volumetrically to the third power. We seem thus
to have arrived at nine
dimensions__i.e., ninth powering__and we have altogether
identified geometrical
realization as being at least nine-dimensional.
|
|
|
986.220
This is how I came to adopt my ninth-power factor for
conversion from XYZ
coordination to synergetics coordination. Employing
the XYZ coordinated volume of
4.188790205, I multiplied it by the appropriate factor
(see table
986.209, where we find
that S9 = 1.193242693), which produced the inherently
imperfect (only chord-describable
rather than arc-describable) sphere of 4.998243305.
This I knew was not a primitive three-
dimensional or six-dimensional volume, and I assumed
it to be the value of potential
energy embraceable by a sphere of vector radius = 1.
Ergo, both my conscious and
subconscious searchings and accountings were operating
faultlessly, but I was confusing
the end product, identifying it as volume instead of
as potential energy.
|
|
|
986.221
I was astonished by my error but deeply excited by
the prospect of reviewing
the exponentially powered values. Looking over the remaining
valid trail blazings, I
ruminated that the proximity to 5 that provoked the
4.998243305 figure might have other
significance__for instance, as a real ninth-dimensional
phenomenon. There was some
question about that constant 1.193242693 being a sixth-dimension
figure: N3 · N3 = N6,
which operation I had__in my forgetfulness and carelessness__inadvertently
performed.
Or the figure I had arrived at could be taken as nine-dimensional
if you assume primitive
demonstrability of minimum something always to have
a combined a priori volumetric-
and-energetic existence value, which is indeed what
synergetics vectorial structuring does
recognize to be naturally and demonstrably true. (See
Sec.
100.20.)
|
|
|
986.222
Synergetics demonstrates that the hierarchy of vectorially
defined, primitive,
triangularly self-stabilized, structural-system polyhedra
is initially sixth-dimensional, being
both a vectorially six-way coordinate system (mass ×
velocity) as well as being
tetrahedrally__ergo,
four-dimensionally-coordinate4 __ergo,
N6 · N4 = N10 somethings;
and that they grow expansively in time-size__ergo, in
volume at the rate of F3 __ergo, in
time-size D10 D3 = D13,
a 13-dimensional special-case-somethingness
of reality.
(Footnote 4: It was a mathematical requirement of XYZ rectilinear coordination that in order to demonstrate four-dimensionality, a fourth perpendicular to a fourth planar facet of the symmetric system must be found--which fourth symmetrical plane of the system is not parallel to one of the already-established three planes of symmetry of the system. The tetrahedron, as synergetics' minimum structural system, has four symmetrically interarrayed planes of symmetry--ergo, has four unique perpendiculars--ergo, has four dimensions.) |
|
|
986.223
We have learned in synergetics by physical experiment
that in agglomerating
unit-radius, closest-packed spheres around a nuclear
sphere of the same unit radius,
successively concentric symmetrical layers of the nuclear
surroundment occur in a pattern
in which the number of spheres in the outer shell is
always the second power of the
frequency of modular-system subdivision of the vector-defined
edges of the system, and
that when the primitive interhierarchy's relative volumetric
values are multiplied by
frequency to the third power__and an additional factor
of six__it always gives the
symmetrical system's total cumulative volume growth,
not only of all its progressively
concentric, closest-packed, unit-radius spheres' combined
shells, but also including the
volume of the unit-radius, closest-packed sphere shells'
interstitial spaces, as altogether
embraced by the exterior planes of the primitive polyhedra
of reference. (See Sec.
971
and, in the drawings section, Fig.
970.20, "Dymax Nuclear
Growth" (10 June 1948), and
"Light Quanta Particle Growth" (7 May 1948); also drawings
published in 1944 appearing
as end papers to Synergetics 2.)
|
|
|
986.230
System Spinnability
|
|
|
986.231
Synergetics assumes an a priori to time-size, conceptually
primitive, relative
volumetric value of all the hierarchy of primitive polyhedra;
and it also assumes that when
we introduce frequency, we are also introducing time
and size (see Secs.
782.50
and
1054.70),
and we are therefore also introducing all
the degrees of freedom inherent in
time-size realizations of energetic-system behavior__as
for instance the phenomenon of
inherent system spinnability.
|
|
|
986.232
With the introduction of the phenomenon of system spinnability
around any
one or several or all of the hierarchy of concentric
symmetric systems' seven axes of
symmetry (Sec.
1040
), we observe experientially that
such inherent system spinnability
produces a superficially spherical appearance, whose
time-size realizations might be
thought of as being only the dynamic development in
time-size aspects of the primitive
static polyhedral states. We recall the scientific nondemonstrability
of the Greek sphere as
defined by them (Secs.
981.19
and
1022.11). We also
recall having discovered that the
higher the frequency of the unit-radius-vertexed, symmetrical
polyhedra of our primitive
cosmic hierarchy, the more spherical do such geodesic-structured
polyhedra appear
(compare Sec.
986.064). I realized that under these
recalled circumstances it could be
safely assumed that a sphere does not exist in the primitive
hierarchy of pre-time-size
polyhedral conceptioning, whose timeless-sizeless__ergo,
eternal__perfection alone
permitted consideration of the vector equilibrium's
isotropic vector matrix as the four-
dimensional frame of reference of any time-size intertransforming
aberrations of realizable
physical experience. Such perfection can be only eternal
and timeless.
|
|
|
986.233
Timeless but conceptually primitive polyhedra of differently-lengthed-and-
radiused external vertexes can be dynamically spinnable
only in time, thereby to produce
circular profiles some of whose longer radii dominantly
describe the superficial, illusory
continuity whose spherical appearance seems to be radially
greater than half the length of
the prime vector. (See Fig.
986.314.)
|
|
|
986.234
Thus the only-superficially-defined spherical appearance
is either the
consequence of the multiplicity of revolving vertexes
of the polyhedron occurring at a
distance outwardly of the unit vector radius of the
prime polyhedral hierarchy, or it could
be inherent in the centrifugal deformation of the polyhedral
structure. Wherefore I realized
that my having unwittingly and redundantly applied the
synergetics constant of the sixth
power__rather than only of the third power__and my having
applied that sixth-power
factor to the theretofore nonexistent static sphere
of the Greeks' energy-and-time deprived
three-dimensionality, was instinctively sound. Thus
the erroneous result I had obtained
must not discourage my intuitive urge to pursue the
question further. I had inadvertently
produced the slightly-greater-than-vector-radiused,
highfrequency "spheric" polyhedron.
|
|
|
986.235
It seemed ever more evident that it could be that there
is no true sphere in
Universe. This seemed to be confirmed by the discovery
that the sum of the angles around
all the vertexes of any system will always be 720 degrees__one
tetra__less than the
number of the system's external vertexes times 360 degrees
(Sec.
224). It could be that
the concept conjured up by the mouthed-word sphere itself
is scientifically invalid; ergo, it
could be that the word sphere is not only obsolete but
to be shunned because it is
meaningless and possibly disastrously misleading to
human thought.
|
|
|
986.240
The Sphere Experimentally Defined
|
|
|
986.241
The best physically demonstrable definition of the
"spheric" experience is: an
aggregate of energy events approximately equidistant,
multidirectionally outwardly from
approximately the same central event of an only approximately
simultaneous set of
external events-the more the quantity of external points
measuringly identified and the
more nearly simultaneous the radius-measuring events,
the more satisfactorily "spherical."
With each of all the outward unit-radius events most
economically and most fully
triangularly interchorded with their most immediate
neighbors__chords being shorter than
their corresponding arcs__we find that the "spheric"
experience inherently describes only
high-frequency, omnitriangularly faceted polyhedra.
By geometrical definition these are
geodesic structures whose volumes will always be something
less than a theoretically
perfect omni-arc-embraced sphere of the same radius
as an omni-chord-embraced
geodesic sphere's uniformly radiused outer vertexes.
|
|
|
986.242
As is demonstrated in Sec.
224, the sum of the angles
around all the vertexes
of any system will always be 720 degrees less than the
number of vertexes multiplied by
360 degrees. By the mathematicians' definition a perfect
arc-embraced sphere would have
to have 360 degrees around every point on its surface,
for the mathematicians assume that
for an infinitesimal moment a sphere's surface is congruent
with the tangent plane.
Trigonometry errs in that it assumes 360 degrees around
every spherical surface point.
|
|
|
986.300
Minimum-Maximum System Limits
|
|
|
986.301
Consideration 11: Maximum-limit Case
|
|
|
986.302
The explorer gains assurance by discovering the relevant
minimum-maximum
limit cases__the min-max limits of the variables__of the
system under consideration.
|
|
|
986.303
For instance, we have learned through experimental
evidence, the cosmic
hierarchy of primitive polyhedra has a limit set of
seven axes of great-circle symmetries
and spinnabilities. They are the 3, 4, 6 (VE), 12, 10,
15, 6 (icosa) great-circle-spinnable
systems. (See Table
986.304
and Sec.
1040.) Within that
inherently limited hierarchy of
seven symmetries, the triacontahedron, with its 15 different
great circles' self-
hemispherings and 120 triangular interconfigurings,
produces the maximum-limit number
of identical polyhedral surface self-facetings of all
great-circle systems in Universe (Sec.
400).
|
|
|
Table 986.304: Limit Set of Seven Axes of Spinnability |
| Next Section: 986.310 |