Characteristics of Tetrahedra
|
|
986.060
Characteristics of Tetrahedra
|
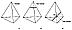 Fig. 986.061 |
986.061
The tetrahedron is at once both the simplest system
and the simplest
structural system in Universe (see Secs.
402
and
620).
All systems have a minimum set of
topological characteristics of vertexes, faces, and
edges (see Secs.
1007.22
and
1041.10).
Alteration of the minimum structural system, the tetrahedron,
or any of its structural-
system companions in the primitive hierarchy (Sec.
982.61),
may be accomplished by
either external or internal contact with
other systems__which
other systems may cleave,
smash, break, or erode the simplest primitive systems.
Other such polyhedral systems may
be transformingly developed by wind-driven sandstorms
or wave-driven pebble beach
actions. Those other contacting systems can alter the
simplest
primitive systems in only two topological-system ways:
|
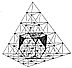 Fig. 1086.062 |
986.062
As we have learned regarding the "Platonic solids"
carvable from cheese
(Sec.
623.10),
slicing a polyhedron parallel to one
of its faces only replaces the original
face with a new face parallel to the replaced face.
Whereas truncating a vertex or an edge
eliminates those vertexes and edges and replaces them
with faces__which become
additional faces effecting a different topological abundance
inventory of the numbers of
vertexes and edges as well. For every edge eliminated
by truncation we gain two new
edges and one new face. For every corner vertex eliminated
by truncation our truncated
polyhedron gains three new vertexes, three new edges,
and one new face.
|
|
|
986.063
The cheese tetrahedron (Sec.
623.13) is the only one
of the primitive
hierarchy of symmetrical polyhedral systems that, when
sliced parallel to only one of its
four faces, maintains its symmetrical integrity. It
also maintains both its primitive
topological and structural component inventories when
asymmetrically sliced off parallel
to only one of its four disparately oriented faces.
When the tetrahedron has one of its
vertexes truncated or one of its edges truncated, however,
then it loses its overall system
symmetry as well as both its topological and structural
identification as the structurally and
topologically simplest of cosmic systems.
|
|
|
986.064
We may now make a generalized statement that the simplest
system in
Universe, the tetrahedron, can be design-altered and
lose its symmetry only by truncation
of one or more of its corners or edges. If all the tetrahedron's
four vertexes and six edges
were to be similarly truncated (as in Fig.
1041.11)
there would result a symmetrical
polyhedron consisting of the original four faces with
an addition of 10 more, producing a
14-faceted symmetrical polyhedron known as the tetrakaidecahedron,
or Kelvin's "solid,"
which (as shown in Sec.
950.12
and Table
954.10) is
an allspace filler__as are also the
cube, the rhombic dodecahedron, and the tetrahedral
Mites, Sytes, and Couplers. All that
further external alteration can do is produce more vertex
and edge truncations which make
the individual system consist of a greater number of
smaller-dimension topological aspects
of the system. With enough truncations__or knocking off
of corners or edges__the system
tends to become less angular and smoother (smoother
in that its facets are multiplying in
number and becoming progressively smaller and thus approaching
subvisible
identification). Further erosion can only "polish off"
more of the only-microscopically-
visible edges and vertexes. A polished beach pebble,
like a shiny glass marble or like a
high-frequency geodesic polyhedral "spheric" structure,
is just an enormously high-
frequency topological inventory-event system.
|
|
|
986.065
Joints, Windows, and Struts: As we have partially noted
elsewhere (Secs.
536 and
604),
Euler's three primitive topological characteristics__texes,
faces, and
lines__are structurally identifiable as joints, windows,
and push-pull struts, respectively.
When you cannot see through the windows (faces), it
is because the window consists of
vast numbers of subvisible windows, each subvisible-magnitude
window being strut-
mullion-framed by a complex of substructural systems,
each with its own primitive
topological and structural components.
|
|
|
986.066
Further clarifying those structural and topological
primitive componentation
characteristics, we identify the structural congruences
of two or more joined-together-
systems' components as two congruent single vertexes
(or joints) producing one single,
univalent, universal-joint intersystem bonding. (See
Secs.
704,
931.20, and Fig.
640.41B.)
Between two congruent pairs of interconnected vertexes
(or joints) there apparently runs
only one apparent (because congruent) line, or interrelationship,
or push-pull strut, or
hinge.
|
|
|
986.067
Returning to our early-Greek geometry initiative and
to the as-yet-persistent
academic misconditioning by the Greeks' oversights and
misinterpretations of their visual
experiences, we recall how another non-Ionian Greek,
Pythagoras, demonstrated and
"proved" that the number of square areas of the unit-module-edged
squares and the
number of cubical module volumes of the unit-module-edged
cubes correspond exactly
with arithmetic's second-powerings and third-powerings.
The Greeks, and all
mathematicians and all scientists, have ever since misassumed
these square and cube
results to be the only possible products of such successive
intermultiplying of geometry's
unit-edge-length modular components. One of my early
mathematical discoveries was the
fact that all triangles__regular, isosceles, or scalene__may
be modularly subdivided to
express second-powering. Any triangle whose three edges
are each evenly divided into the
same number of intervals, and whose edge-interval marks
are cross-connected with lines
that are inherently parallel to the triangle's respective
three outer edges__any triangle so
treated will be subdivided by little triangles all exactly
similar to the big triangle thus
subdivided, and the number of small similar triangles
subdividing the large master triangle
will always be the second power of the number of edge
modules of the big triangle. In
other words, we can say "triangling" instead of "squaring,"
and since all squares are
subdivisible into two triangles, and since each of those
triangles can demonstrate areal
second-powering, and since nature is always most economical,
and since nature requires
structural integrity of her forms of reference, she
must be using "triangling" instead of
"squaring" when any integer is multiplied by itself.
(See Sec.
990.)
|
|
|
986.068
This seemed to be doubly confirmed when I discovered
that any
nonequiedged quadrangle, with each of its four edges
uniformly subdivided into the same
number of intervals and with those interval marks interconnected,
produced a pattern of
dissimilar quadrangles. (See Fig.
990.01.) In the same
manner I soon discovered
experimentally that all tetrahedra, octahedra, cubes,
and rhombic dodecahedra__regular or
skew__could be unitarily subdivided into tetrahedra with
the cube consisting of three
tetra, the octahedron of four tetra, and the rhombic
dodecahedron of six similar tetra; and
that when any of these regular or skew polyhedras' similar
or dissimilar edges and faces
were uniformly subdivided and interconnected, their
volumes would always be uniformly
subdivided into regular or skew tetrahedra, and that
N3 could and should be written and
spoken of as Ntetrahedroned and not as Ncubed.
|
|
|
986.069
Nature would use the tetrahedron as the module of subdivision
because
nature has proven to the physicists and the other physical
scientists that she always
chooses the most economic realization. Cubes require
three times as much Universe as do
tetrahedra to demonstrate volumetric content of systems
because cubic identification with
third-powering used up three times as much volume as
is available in Universe. As a result
of cubic mensuration science has had to invent such
devices as "probability" and
"imaginary numbers." Thus "squaring" and "cubing," instead
of nature's "triangling" and
"tetrahedroning," account for science's using mathematical
tools that have no physical-
model demonstrability__ergo, are inherently "unscientific."
|
|
|
986.070
Buildings on Earth's Surface
|
|
|
986.071
In the practical fortress and temple building of the
earliest known
Mesopotamians, Egyptians, and Greeks their cubes and
omnirectilinear blocks seemed
readily to fill allspace as they were assembled into
fortress or temple walls with plumb
bobs, water-and-bubble levels, straightedges, and right-triangle
tools. No other form they
knew__other than the cube__seemed to fill allspace as
demonstrated in practical masonry;
wherefore they assumed this to be scientifically demonstrated
proof of the generalizability
of their mathematically abstracted plane- and solid-geometry
system and its XYZ
coordination.
|
|
|
986.072
Because of the relatively diminutive size of humans
in respect to the size of
our planet, world-around society as yet spontaneously
cerebrates only in terms of our
immediate world's seeming to demonstrate itself to be
a flat plane base, all of the
perpendiculars of which__such as trees and humans and
human-built local structures-
appear to be rising from the Earth parallel to one another__ergo,
their ends point in only
two possible directions, "up" or "down." . . . It's
"a wide, wide world," and "the four
corners of the Earth."
|
|
|
986.073
It was easy and probably unavoidable for humanity to
make the self-
deceptive blunders of assuming that a cube held its
shape naturally, and not because the
stone-cutters or wood-cutters had chosen quite arbitrarily
to make it in this relatively
simple form. Human's thought readily accepted__and as
yet does__the contradictory
abstract state "solid." The human eye gave no hint of
the energetic structuring of the
atomic microcosm nor of the omnidynamic, celestial-interpositioning
transformations of
both macro- and micro-Universe.
|
|
|
986.074
Prior to steel-framed or steel-reinforced-concrete
construction methods,
humans' buildings that were constructed only of masonry
could not be safely built to a
height of over 20 stories__approximately 200 feet high.
Such a masonry building was
Chicago's turn-of-the-20th-century world-record Monadnock
Building, whose base
covered a small but whole city block. It is not until
we reach a height of 100
stories__approximately 1000 feet high__that two exactly
vertical square columns, each
with base edges of 250 feet, built with exactly vertical
walls, and touching one another
only along one of each of their base edges, will show
a one-inch space between them. The
rate their vertical walls part from one another is only
1/1000th of an inch for each
foot of height.
|
|
|
986.075
Masons' and carpenters' linear measuring devices are
usually graduated only
to 1/16th of an inch, and never finer than 1/32nd of
an inch. Thus differentials of a
thousandth of an inch are undetectable and are altogether
inadvertently overlooked; ergo,
they get inadvertently filled-in, or cross-joined, never
to have been known to exist even on
the part of the most skilled and conscientious of building
craftsmen, whose human eyes
cannot see intervals of less than 1/100th of an inch.
|
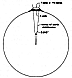 Fig. 986.076 |
986.076
If two exactly-vertical-walled city skyscrapers are
built side by side, not until
they are two and one-half miles high (the height of
Mount Fuji) will there be a space of
one foot between the tops of their two adjacent walls.
(See Fig.
986.076.) Of course, the
farther apart the centers of their adjacent bases, the
more rapidly will the tops of such high
towers veer away from one another:
(Footnote 2: The Engineer (New York: Time-Life Books, 1967.) If the towers are 12,000 miles apart-that is, halfway around the world from one another-their tops will be built in exactly opposite directions ergo, at a rate of two feet farther apart for each foot of their respective heights.) |
|
|
986.077
It is easy to understand how humans happened to think
it "illogical" to have
to consider that all the perpendiculars to a sphere
are radii of that sphere__ergo, never
parallel to one another. Our humans-in-Universe scale
is inherently self-deceptive__ergo,
difficult to cope with rigorously.
|
|
|
986.080
Naive Perception of Childhood
|
|
|
986.081
The inventory of experimentally demonstrated discoveries
of science which
had accrued by the time of my childhood gave me reason
to question many of the
"abstractions" of geometry as I was being instructed
in that subject. Axioms were based
on what only seemed "self-evident," such as the stone
block or the "cubical" wooden play
blocks of my nursery. To society they "obviously held
their shape." I do not think that I
was precocious or in any way a unique genius. I had
one brother; he was three years
younger than I. His eyesight was excellent; mine was
atrocious. I did not get my first
eyeglasses until my younger brother was running around
and talking volubly. He could see
things clearly; I could not. Our older sister could
also see things clearly. I literally had to
feel my way along__tactilely__in order to recognize the
"things" of my encountered
environment-ergo, my deductions were slow in materializing.
My father called my
younger brother "stickly-prickly" and he called me "slow-and-solid"-terms
he adopted
from "The Jaguar and the Armadillo" in Kipling's Just
So Stories.
|
|
|
986.082
I was born cross-eyed on 12 July 1895. Not until I
was four-and-a-half years
old was it discovered that I was also abnormally farsighted.
My vision was thereafter fully
corrected with lenses. Until four-and-a-half I could
see only large patterns__houses, trees,
outlines of people__with blurred coloring. While I saw
two dark areas on human faces, I
did not see a human eye or a teardrop or a human hair
until I was four. Despite my newly
gained ability__in 1899__to apprehend details with glasses,
my childhood's spontaneous
dependence upon only big-pattern clues has persisted.
All that I have to do today to
reexperience what I saw when I was a child is to take
off my glasses, which, with some
added magnification for age, have exactly the same lens
corrections as those of my first
five-year-old pair of spectacles. This helps me to recall
vividly my earliest sensations,
impressions, and tactical assumptions.
|
|
|
986.083
I was sent to kindergarten before I received my first
eyeglasses. The teacher,
Miss Parker, had a large supply of wooden toothpicks
and semidried peas into which you
could easily stick the sharp ends of the toothpicks.
The peas served as joints between the
toothpicks. She told our kindergarten class to make
structures. Because all of the other
children had good eyesight, their vision and imagination
had been interconditioned to
make the children think immediately of copying the rectilinearly
framed structures of the
houses they saw built or building along the road. To
the other children, horizontally or
perpendicularly parallel rectilinear forms were structure.
So they used their toothpicks and
peas to make cubic and other rectilinear models. The
semidried peas were strong enough
to hold the angles between the stuck-in toothpicks and
therefore to make the rectilinear
forms hold their shapes__despite the fact that a rectangle
has no inherent self-structuring
capability.
|
|
|
986.084
In my poor-sighted, feeling-my-way-along manner I found
that the
triangle__I did not know its name-was the only polygon__I
did not know that word
either-that would hold its shape strongly and rigidly.
So I naturally made structural
systems having interiors and exteriors that consisted
entirely of triangles. Feeling my way
along I made a continuous assembly of octahedra and
tetrahedra, a structured complex to
which I was much later to give the contracted name "octet
truss." (See Sec.
410.06). The
teacher was startled and called the other teachers to
look at my strange contriving. I did
not see Miss Parker again after leaving kindergarten,
but three-quarters of a century later,
just before she died, she sent word to me by one of
her granddaughters that she as yet
remembered this event quite vividly.
|
|
|
986.085
Three-quarters of a century later, in 1977, the National
Aeronautics and
Space Administration (NASA), which eight years earlier
had put the first humans on the
Moon and returned them safely to our planet Earth, put
out bids for a major space-island
platform, a controlled-environment structure. NASA's
structural specifications called for
an "octet truss" __my invented and patented structural
name had become common
language, although sometimes engineers refer to it as
"space framing." NASA's scientific
search for the structure that had to provide the most
structural advantages with the least
pounds of material__ergo, least energy and seconds of
invested time-in order to be
compatible and light enough to be economically rocket-lifted
and self-erected in
space__had resolved itself into selection of my 1899
octet truss. (See Sec.
422.)
|
|
|
986.086
It was probable also that my only-insectlike, always-slow,
cross-referencing
strategy of touching, tasting, smelling, listening,
and structurally testing by twisting and
pounding and so forth__to which I spontaneously resorted__made
me think a great deal
about the fact that- when I broke a piece of glass or
a stone or a wooden cube apart, it did
not separate naturally into little cubes but usually
into sharp pointed shapes. In the earliest
of my memories I was always suspicious of the integrity
of cubes, which only humans
seemed to be introducing into the world. There were
no cubical roses, eggs, trees, clouds,
fruits, nuts, stones, or anything else. Cubes to me
were unnatural: I observed humans
deliberately sawing ice into large rectilinear cakes,
but window glass always broke itself
into predominantly triangular pieces; and snowflakes
formed themselves naturally into a
myriad of differently detailed, six-triangled, hexagonal
patterns.
|
|
|
986.087
I was reacting normally in combining those spontaneous
feelings of my
childhood with the newly discovered knowledge of the
time: that light has speed (it is not
instantaneous, and comes in smallest packages called
photons); that there is something
invisible called electricity (consisting of "invisible
behaviors" called electrons, which do
real work); and that communication can be wireless,
which Marconi had discovered the
year I was born__and it is evident that I was reacting
normally and was logically unable to
accept the customarily honored axioms that were no longer
"self-evident."
|
|
|
986.088
My contemporaries and I were taught that in order to
design a complete and
exact sphere and have no materials left over, we must
employ the constant known as pi
(pi), which I was also taught was a "transcendentally
irrational number," meaning it could
never be resolved. I was also informed that a singly
existent bubble was a sphere; and I
asked, To how many places does nature carry out pi when
she makes each successive
bubble in the white-cresting surf of each successive
wave before nature finds out that pi
can never be resolved? . . . And at what moment in the
making of each separate bubble in
Universe does nature decide to terminate her eternally
frustrated calculating and instead
turn out a fake sphere? I answered myself that I don't
think nature is using pi or any of the
other irrational fraction constants of physics. Chemistry
demonstrates that nature always
associates or disassociates in whole rational increments....
Those broken window shards
not only tended to be triangular in shape, but also
tended to sprinkle some very fine
polyhedral pieces. There were wide ranges of sizes of
pieces, but there were no pieces that
could not "make up their minds" or resolve which share
of the original whole was theirs.
Quite the contrary, they exploded simultaneously and
unequivocally apart.
|
|
|
986.089
At first vaguely, then ever more excitedly, precisely,
and inclusively, I began
to think and dream about the optimum grand strategy
to be employed in discovering
nature's own obviously elegant and exquisitely exact
mathematical coordinate system for
conducting the energetic transactions of eternally regenerative
Universe. How does nature
formulate and mass-produce all the botanical and zoological
phenomena and all the
crystals with such elegant ease and expedition?
|
| Next Section: 986.090 |